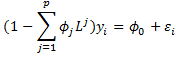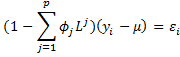Lag Function

Basic Concept

We now define the lag function as

Here, we assume that

for any constant c and any variables x and z. We also use the following notation for any variable z and non-negative integer n.

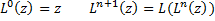AR(p) process

We can express the AR(p) process

using the lag function notation as

or even

Here 1 is the identity function and we use the notation (f+g)x to mean f(x) + g(x) for any functions f and g. Using this notation, we can also express an AR(p) process by

By Property 1 of Autoregressive Process Basic Concepts, this is equivalent to

or

Note that

is a p^th degree polynomial which is equivalent to the characteristic polynomial of the AR(p) process, as described in Characteristic Equation for Autoregressive Processes. This polynomial can be factored (by the Fundamental Theorem of Algebra) as follows

where the values r₁, r₂, …, r_p are the characteristic roots of the AR(p) process.

Based on the vector φ = [φ₁, …, φ_p] of coefficients, we can define the operator φ(L)

and so an autoregression process can be expressed succinctly as

Final Note

The lag function is also called the (back) shift operator and so sometimes the symbol B is used in place of L.

References

Greene, W. H. (2002) Econometric analysis. 5th Ed. Prentice-Hall
https://www.scirp.org/(S(351jmbntvnsjt1aadkposzje))/reference/referencespapers.aspx?referenceid=1243286

Gujarati, D. & Porter, D. (2009) Basic econometrics. 5th Ed. McGraw Hill
http://www.uop.edu.pk/ocontents/gujarati_book.pdf

Hamilton, J. D. (1994) Time series analysis. Princeton University Press
https://press.princeton.edu/books/hardcover/9780691042893/time-series-analysis

Wooldridge, J. M. (2009) Introductory econometrics, a modern approach. 5th Ed. South-Western, Cegage Learning
https://cbpbu.ac.in/userfiles/file/2020/STUDY_MAT/ECO/2.pdf