Finding AR(p) coefficients

Basic Concepts

Suppose that we believe that an AR(p) process is a fit for some time series. We now show how to calculate the process coefficients using the following techniques: (1) estimates based on ACF or PACF values, (2) using linear regression and (3) using Solver.

We illustrate the first of these approaches on this webpage. The second is described at Finding AR(p) Coefficients using Regression, and, finally, the third is explained at Calculate ARMA(p,q) Coefficients using Solver.

For approach 1, we use the Yule-Walker equations in reverse to calculate the φ₀, φ₁, …, φ_p, σ² coefficients based on the values of μ, γ₀, …, γ_p (ACF values). Alternatively, we can use the values μ, γ₀, π₁…, π_p (PACF values), which it turns out are equivalent.

Essentially, this is the method of moments.

AR(1) Example

Example 1: Use the statistics described above to find the coefficients of the AR(1) process based on the data in Example 1 of Autoregressive Processes Basic Concepts.

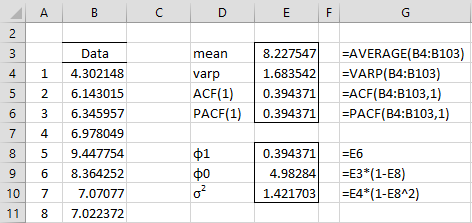
The first 8 of 100 data elements are shown in column B of Figure 1. We next calculate the mean, variance and PACF(1) values. From these, we can estimate the process coefficients as shown in cells G8:G10. This estimate of the time series is the process y_i = 4.983 + .394y_i-1 + ε_i where σ² = 1.421703.

Figure 1 – Estimation of AR(1) coefficients

As we can see, the process coefficients are pretty close to the original coefficients used to generate the data in column B (φ₀ = 5, φ₀ = .4 and σ² = 1) with the exception of σ², which is a little high.

Observation

We can use this approach for AR(2) processes, by noting that

Thus

and so

Alternatively, we could use the following equivalences: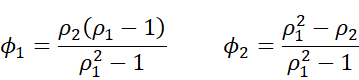

AR(2) Example

Example 2: Use the statistics described above, to find the coefficients of the AR(2) process based on the data in Example 1.

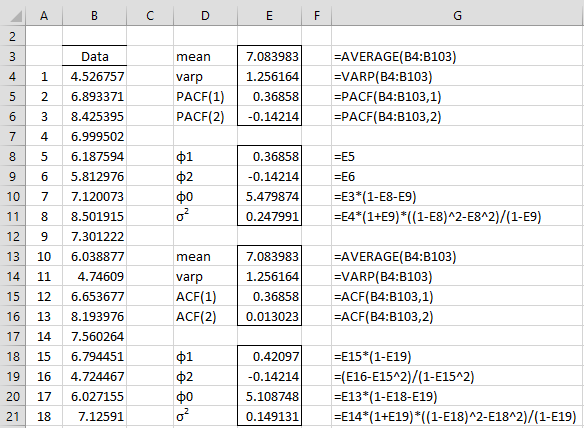
We show two versions in Figure 2. The lower version is based on the ACF using the formulas described in the above observation. The upper version is based on the PACF using Property 1 of Partial Autocorrelation of AR(p) Processes.

Figure 2 – Estimation of AR(2) coefficients

Estimate of σ²

When using the method of moments approach to estimating the AR(p) coefficients, we can estimate the variance of the error terms via the following formula:

where s² is the usual expression for the variance of the time series

From the above, we see that for AR(1)

Examples Workbook

Click here to download the Excel workbook with the examples described on this webpage.

References

Wikipedia (2016) Autoregressive model
https://en.wikipedia.org/wiki/Autoregressive_model

Djellouli, A. (2024) Autoregressive (AR) models in time series analysis
https://adamdjellouli.com/articles/statistics_notes/time_series_analysis/autoregressive_models

Hamilton, J. D. (1994) Time series analysis. Princeton University Press
https://press.princeton.edu/books/hardcover/9780691042893/time-series-analysis