Property 1: The mean of the yi in a stationary AR(p) process is
Proof: Since the process is stationary, for any k, E[yi] = E[yi-k], a value which we will denote μ. Since E[εi] = 0, E[φ0] = φ0 and
it follows that
Solving for μ yields the desired result.
Property 2: The variance of the yi in a stationary AR(1) process is
Proof: Since the yi and εi are independent, by basic properties of variance, it follows that
Since the process is stationary, var(yi) = var(yi-1), and so
Solving for var(yi) yields the desired result.
Property 3: The lag h autocorrelation in a stationary AR(1) process is
Proof: First note that for any constant a, cov(a+x, a+y) = cov(x,y). Thus, cov(yi,yj) has the same value even if we assume that φ0 = 0, and similarly for var(yi) = cov(yi,yi). Thus, it suffices to prove the property when φ0 = 0. In this case, by Property 1, μ = 0, and so cov(yi,yj) = E[yiyj].
Thus
since by the stationary property, E[yi-1,yi-k] = γi-1. Now, by induction on k, it is easy to see that
Hence
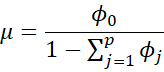
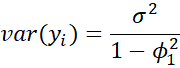
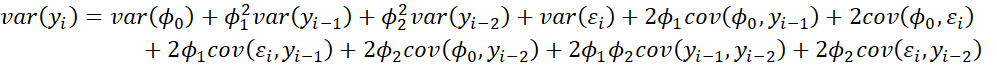
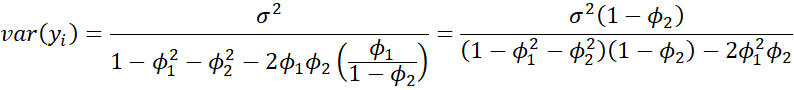
I love that you have proofs here, and I love the format. This has been useful for my final exam study for my time-series course. Many textbooks only provide proofs for the general AR(p) case, which makes it more difficult to follow, and frustrating when I know how to use the formula.
Dear Charles, In Property 2 proof, line 6. It mentioned the below.
“Since the process is stationary, yi = yi-1, and so”. Would you please elaborate how true this statement is ? Shouldn’t the statement states that, Since the process is stationary, var(yi)=var(yi-1), and so ?
Hello Ranil,
Yes, of course you are correct. Thanks for identifying this error. I have now corrected the webpage.
Thanks for bringing this error to my attention.
Charles
You are welcome Charles.
Dear Sir,
By when will you be able to post all the proofs…….
Pankaj,
After I finish with Release 5.3 of the Real Statistics software.
Charles
please post the proof.
Pankaj,
Sorry, but it looks like I forgot to add this webpage. I am now finishing up the testing for the next release of the Real Statistics software (rel 5.3). When I have finished this, I will add the missing proofs.
Charles