Definitions
In a simple linear regression model, the dependent variable is modeled as a linear function of the independent variable plus a random error term.
Similarly, a first-order autoregressive process, denoted AR(1), takes the form
Thinking of the subscripts i as representing time, we see that the value of y at time i is a linear function of y at time i-1 plus a fixed constant and a random error term. Similar to the ordinary linear regression model, we assume that the error terms are independently distributed based on a normal distribution with zero mean and a constant variance σ2, and that the error terms are independent of the y values. Thus
εi ∼ N(0, σ2)
cov(εi , εj) = 0 for i ≠ j cov(εi, yj) = 0 for i, j
It turns out that such a process is stationary when |φ1| < 1, and so we will make this assumption as well. Note that if |φ1| = 1, we have a random walk.
Similarly, a second-order autoregressive process, denoted AR(2), takes the form
In general, a p-order autoregressive process, AR(p), takes the form
Basic Properties
Property 1: The mean of the yi in a stationary AR(p) process is
Proof: click here
Property 2: The variance of the yi in a stationary AR(1) process is
Proof: click here
Property 3: The lag h autocorrelation in a stationary AR(1) process is
Proof: click here
Example
Example 1: Simulate a sample of 100 elements from the AR(1) process
where εi ∼ N(0,1) and calculate ACF.
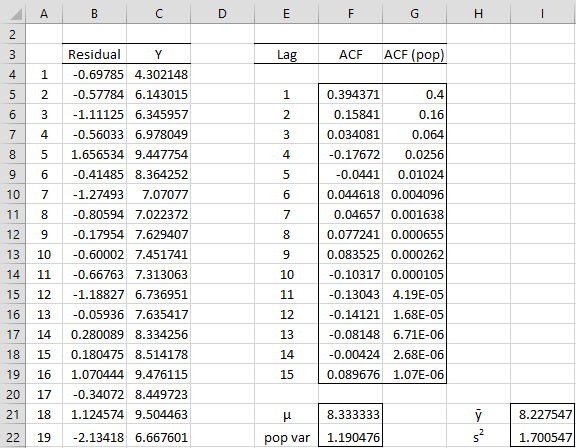
Thus φ0 = 5, φ1 = .4 and σ = 1. We simulate the independent εi by using the Excel formula =NORM.INV(RAND(),0,1) or =NORM.S.INV(RAND()) in column B of Figure 1 (only the first 20 of 100 values are displayed.
The value of y1 is calculated by placing the formula =5+0.4*0+B4 in cell C4 (i.e. we arbitrarily assign the value zero to y0). The other yi values are calculated by placing the formula =5 +0.4*C4+B5 in cell C5, highlighting the range C5:C203, and pressing Ctrl-D.
By Properties 1 and 2, the theoretical values for the mean and variance are μ = φ0/(1–φ1) = 5/(1–.4) = 8.33 (cell F22) and
(cell F23). These compare to the actual time series values of ȳ =AVERAGE(C4:C103) = 8.23 (cell I22) and s2 = VAR.S(C4:C103) = 1.70 (cell I23).
The time series ACF values are shown for lags 1 through 15 in column F. These are calculated from the y values as in Example 1. Note that the ACF value at lag 1 is .394376. Based on Property 3, the population ACF value at lag 1 is ρ1 = φ1 = .4. Theoretically, the values for ρh = = .4h should get smaller and smaller as h increases (as shown in column G of Figure 1).
Figure 1 – Simulated AR(1) process
Charts
The graph of the y values is shown on the left of Figure 2. As you can see, no particular pattern is visible. The graph of ACF for the first 15 lags is shown on the right side of Figure 2. As you can see, the actual and theoretical values for the first two lags agree, but after that, the ACF values are small but not particularly consistent.
Figure 2 – Graphs of simulated AR(1) process and ACF
Observation
Based on Property 3, for 0 < φ1 < 1, the theoretical values of ACF converge to 0. If φ1 is negative, -1 < φ1 < 0, then the theoretical values of ACF also converge to 0, but alternate in sign between positive and negative.
Yule-Walker equations
Property 4 : For any stationary AR(p) process, we can calculate the autocovariance at lag k > 0 by
Similarly, the autocorrelation at lag k > 0 can be calculated as
![]()
Here we assume that γh = γ-h and ρh = ρ-h if h < 0, and ρ0 = 1.
These are known as the Yule-Walker equations.
Proof: click here
Property 5: The Yule-Walker equations also hold, where k = 0 provided we add a σ2 term to the sum. This is equivalent to
Observation: In the AR(1) case, we have
![]()
![]()
![]()
In the AR(2) case, we have![]()
We can also calculate the variance as follows:
Solving for γ0 yields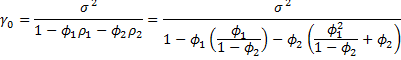
This value can be re-expressed algebraically as described in Property 7 below.
Property 6: The following hold for a stationary AR(2) process
![]()
![]()
Proof: Follows from Property 4, as shown above.
Property 7: The variance of the yi in a stationary AR(2) process is
Proof: click here for an alternative proof.
Examples Workbook
Click here to download the Excel workbook with the examples described on this webpage.
Links
References
Alonso, A. M., Garcia-Martos, C. (2012) Time series analysis: autoregressive, MA and ARMA processes
https://www.academia.edu/35659911/Time_Series_Analysis_Autoregressive_MA_and_ARMA_processes
Greene, W. H. (2002) Econometric analysis. 5th Ed. Prentice-Hall
https://www.ctanujit.org/uploads/2/5/3/9/25393293/_econometric_analysis_by_greence.pdf
Gujarati, D. & Porter, D. (2009) Basic econometrics. 5th Ed. McGraw Hill
http://www.uop.edu.pk/ocontents/gujarati_book.pdf
Hamilton, J. D. (1994) Time series analysis. Princeton University Press
https://press.princeton.edu/books/hardcover/9780691042893/time-series-analysis
Wooldridge, J. M. (2009) Introductory econometrics, a modern approach. 5th Ed. South-Western, Cegage Learning
https://cbpbu.ac.in/userfiles/file/2020/STUDY_MAT/ECO/2.pdf
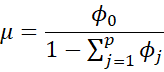
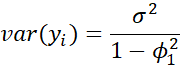

Hi Charles,
Do you have any explanation on why the theoretical variance is lower than the sample (actual) variance ? By Property 1 I can understand why the theoretical mean of the AR (1) gets bigger when phi_1 increases. I cannot draw a similar conclusion for the theoretical variance from Property 2 (one would actually an increase in the theoritical variance as ph_1 increases in absolute value).
Dear Ibrahima,
The formula shows that var(y_i) does increase as phi_1 increases from 0 to 1. Say sigma_1 = 1, then when phi_1 = .5 then var(y_i) = 1.3333, but when phi_i = .6 then var(y_i) = 1.5625.
Charles
I have data that can be described by the model Arima 010. I am not being able to calculate the late and there is no constant in the equation. Please tell me how to go about the same
See https://real-statistics.com/time-series-analysis/arima-processes/
Charles
Hi Charles,
I am trying to follow your tutorial.
I need the data set to follow the excel calculation. How do I find it?
Ahana,
You can download all the examples, including the data, from Download Examples Workbooks
Charles
This is very clear and very helpful!
To assess the effect of a chronic medical condition from which I suffer, each day I give myself a score out of 10, and have been doing so every day for over six years. Though I have a degree in mathematics with a fair proportion of statistics (and a PhD in statistics, in a very specialised area), I know little about time series, but your pages and Excel functions are really helping me to make a start on analysing my data. The next step for me is to formulate a model taking account of the discrete nature of my data.
Keep up the excellent work!
Chris,
Glad I could help.
Charles
Can the method of maximum likelihood estimation be applied to the estimation of the phi parameter using the yule-walker equation?
Jay,
Sorry, but I haven’t covered the topic of the Yule-Walker equations yet.
Charles
is it possible to calculate AR, MA or even ARMA using simple scientific calculator? what is the procedures?
Dan,
Probably so if your scientific calculator has programming capabilities. Otherwise, it will take a fair bit of manual effort.
Charles
Hi Charles – shouldn’t the formula in the text for example 1 say 0.4 instead of 0.5 for “=5 +0.5*C4+B5”
Nick,
Yes, you are correct. I have just corrected this typo.
I appreciate your help in improving the accuracy and usefulness of the website.
Charles
Perhaps I am wrong, but I think that figure 2 left title should be
y(i) = 4 + .4 y(i-1)+ epsilon(i)
Rafael,
Thanks for catching this error. I have now changed the title.
I appreciate your help in improving the website.
Charles