MA(∞) Representation
For an ARMA(1, 1) process
Now let’s suppose that |φ1| < 1. We show how to create the MA(∞) representation as follows:
The MA(∞) representation is therefore
If |φ1| < 1, then this ARMA(1,1) process is stationary. It also turns out that when |θ1| < 1, the process is invertible.
Example 1: Find the MA(∞) form of the ARMA(1, 1) process yi =.4yi-1 +εi – .2εi-1
![]()
![]()
etc.
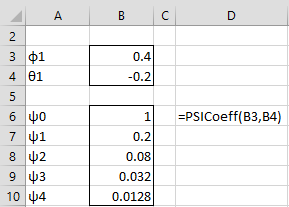
We get the same result using the Real Statistics PSICoeff array function as shown in Figure 1.
Figure 1 – Finding MA(∞) Coefficients
Properties
Property 1: The following is true for an ARMA(1, 1) process
Proof: See ARMA Proofs
Property 2: The following is true for an ARMA(1, 1) process
Proof: See ARMA Proofs
Observation: Since z1 = 1/φ1 is the root of the characteristic polynomial φ(z) = 1 – φ1z, we can express the second term in Property 2 as
It turns out that this can be generalized to other ARMA processes.
Property 3: The following is true for an ARMA(1, 1) process
Proof: See ARMA Proofs
Estimating Coefficients
As we discuss elsewhere, we can use MLE or Solver to estimate the coefficients of an ARMA(1, 1) process. Here we show how to use the ACF to estimate these coefficients.
Given a time series from an ARMA(1, 1) process, we can calculate r1 and r2 as estimates of ρ1 and ρ2. Now by Property 3, ρ2 = ρ1φ1, and so φ1 = ρ2/ρ1. We can now plug these values into the other formula from Property 3
![]()
to obtain an estimate for θ1. In fact, we can express this formula as
Using the quadratic formula, we keep any real invertible solution for θ1, if it exists. We can calculate the variance of the error via the formula
where s2 is the usual expression for the variance of the time series
Restriction
When θ1 = –φ1 for an ARMA(1, 1) process, we note that γ0 = σ2 and ρk = 0 for all k > 1, which are the characteristics of white noise.
In fact, the white noise process with zero mean takes the form
yi = εi
We see that φ1 yi – φ1 εi = 0 for all i, and in particular φ1 yi-1 – φ1 εi-1 = 0. Thus, the process takes the form
which is an ARMA(1,1) process with θ1 = –φ1. In fact, when this ARMA process is expressed in lag format as
φ(L)yi = θ(L)εi
then φ(L) and θ(L) have a common factor, namely 1 – φ1. Henceforth we insist that an ARMA model not have a common factor, and so the above model can’t be expressed as an ARMA(1,1) model.
Simulation (zero mean)
Example 2: Simulate a sample of 105 elements from the ARMA(1, 1) process
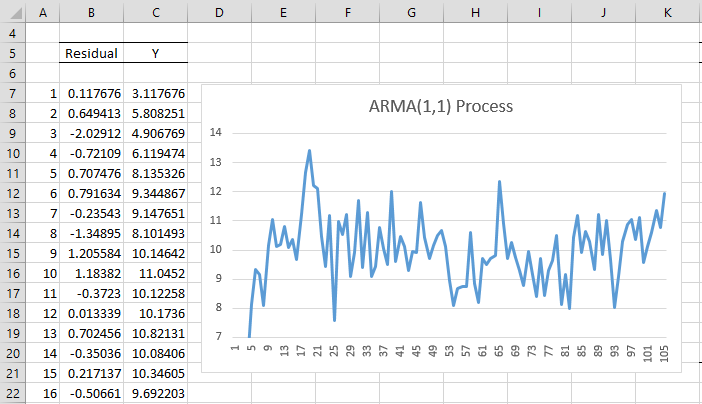
where εi ∼ N(0, 1) and calculate the ACF.
This is done in Figure 2 by placing the formula =NORM.S.INV(RAND()) in cell B7 and the formula =0.7*C6+B7-0.2*B6 in cell C7, highlighting the range B7:C111 and pressing Ctrl-D (only the first 16 elements of the simulation is shown in Figure 2).
Figure 2 – Simulated ARMA(1,1) process
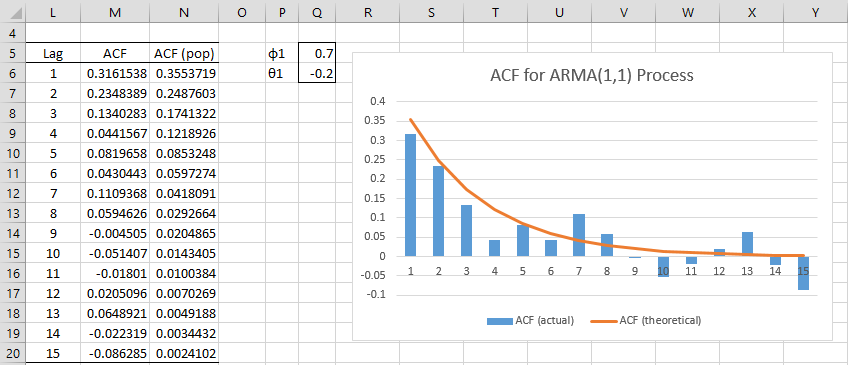
The ACF values are shown in Figure 3 where the theoretical values are based on Property 3.
Figure 3 – ACF for ARMA(1,1) Process
Cell M6 contains the formula =ACF($C$12:$C$111,L6), and similarly, for the other cells in column M, cell N6 contains the formula =(Q5+Q6)*(1+Q5*Q6)/(1+2*Q5*Q6+Q5^2) and cell N7 contains the formula =N6*Q$5, and similarly for rest of the cells in column N.
Since |φ1| = .7 < 1 and |θ1| = .2 < 1, this process is both stationary and invertible.
Simulation (non-zero mean)
Example 3: Simulate a sample of 105 elements from the ARMA(1, 1) process
where εi ∼ N(0, 1) and calculate the ACF.
The only difference between this process and the one in Example 2 is the constant term. The approach is identical, except that this time you place the formula =3+0.7*C6+B7-0.2*B6 in cell C7. The result is shown in Figure 4. Note that the ACF values are identical to those in Figure 3.
Figure 4 – Simulated ARMA(1,1) Process with non-zero mean
Examples Workbook
Click here to download the Excel workbook with the examples described on this webpage.
References
Greene, W. H. (2002) Econometric analysis. 5th Ed. Prentice-Hall
https://www.ctanujit.org/uploads/2/5/3/9/25393293/_econometric_analysis_by_greence.pdf
Gujarati, D. & Porter, D. (2009) Basic econometrics. 5th Ed. McGraw Hill
http://www.uop.edu.pk/ocontents/gujarati_book.pdf
Hamilton, J. D. (1994) Time series analysis. Princeton University Press
https://press.princeton.edu/books/hardcover/9780691042893/time-series-analysis
Wooldridge, J. M. (2009) Introductory econometrics, a modern approach. 5th Ed. South-Western, Cegage Learning
https://cbpbu.ac.in/userfiles/file/2020/STUDY_MAT/ECO/2.pdf
Wei, W. (2006) Time series analysis: univariate and multivariate methods, 2nd edition. Pearson Addison Wesley https://www.researchgate.net/publication/236651810_Time_Series_Analysis_Univariate_and_Multivariate_Methods_2nd_edition_2006
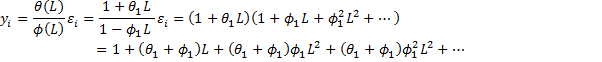
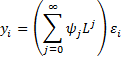
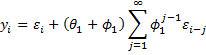
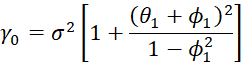

The expression for gamma(0) in Property 1 is wrong, the first term in the bracket is just 1 as in ARMA proofs.
Nazim,
Thank you for catching this error. I have now made the correction on the website.
I appreciate your help in improving the accuracy of the website.
Charles
Hi Charles,
Thank you for your amazing work.
I would like to ask you: in a real dataset, how are the residuals calculated? Are they the residuals from (actual return – AR model predicted return) or something else? Thank you!
Residuals are calculated as shown on the website: observed data value minus the value predicted by the model.
Charles
Hello Mr,
Can you please provide the proof of the property 1 result, the variance of ARMA(1,1) ?
Thank you
mabrouka
Mabrouka,
I have added the proof on the following webpage:
https://real-statistics.com/time-series-analysis/arma-processes/arma-proofs/
Charles
Dear Charles,
I was wondering if the excel-file from “forecasting-arma” is also downloadable, so i could get a better understanding of Example 1 and Example 2.
I am currently working on my master thesis, whereby i want to forecast some dataset i have based on the ARIMA(p,d,q) model. Here for i have succeeded to make a ACF and PaCF of the current and differenced data set. To test different type of ARMINA models i think i need to estimate these parameters for several configurations based on the ACF and PACF results.
Thanks,
Kelvin
Kelvin,
Yes, go to the following webpage and download the Time Series Examples.
Examples Workbooks
Charles