ARMA Processes Basic Concepts

An autoregressive moving average (ARMA) process consists of both autoregressive and moving average terms. If the process has terms from both an AR(p) and MA(q) process, then the process is called ARMA(p, q) and can be expressed as

image205z

orimage206z

We can define an ARMA(p, q) process with zero mean by removing the constant term (i.e. φ0) and saying that y1, …, yn has an ARMA(p, q) process with mean µ if the time series z1, …, zn has an ARMA(p, q) process with zero mean where zi = yi – µ.

If we include the constant term, then as in the AR(p) case, for a stationary ARMA(p, q) process

image053z

An equivalent expression for an ARMA(p, q) process with zero mean is

image207z

which can be expressed using the lag (or backshift) operator as follows

image208z

or even asimage209z

4 thoughts on “ARMA Processes Basic Concepts”

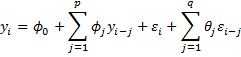
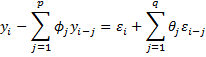
  1. Hi,

    I want to forecast values based on an ARMA(3,3) model. I do not have prior data. How do you calculate values for the error terms? Is there an algorithm to do the calculations for the time series?

    Reply

  2. I was wondering if there is a way to calculate the errors to estimate the coefficients of the MA model. Or if this has to be understood as abstract theorem and get the coefficients with an optimization process. In the literature you have that the MA model is an error model , but it never says how to get the errors in first instance. I understood that the errors came from the AR model, but I am not sure about this idea. In your excel I can see that in the MA sheet, you created a model (equation) and then you get the Y. So, I wonder, can we have a Y vector and then get the errors model from that Y, and then get de coefficients? Thanks for freeing my doubts.

    Reply

Leave a Comment