Property 1: An ARMA(p, q) process
is stationary provided it is causal, i.e. the polynomial
for any z such that |z| ≤ 1.
Observation: Actually, we will only consider stationary ARMA(p, q) processes.
From Property 1, if z is a root of the polynomial 1 – φ1z – φ2z2 – ··· – φpzp, it follows that |z| > 1. As in the AR(p) case, this is equivalent to the fact that |w| < 1 for any w that satisfies the following equation
The causal property implies that (and is equivalent to) the fact that there exist constants ψj such that ψ0 = 1 and
Thus all stationary ARMA processes can be expressed as an MA(∞) process. In fact, the ψj coefficients can be determined as in Property 2.
Property 2: Let
Then
which in turn results in
where θ0 = 1, θj = 0 for j > q and ψj = 0 for j < 0.
Proof: See ARMA Proofs
Observation: We will also restrict our attention to invertible ARMA(p, q) processes, i.e. those for which if 1 + θ1z + θ2z2 + ··· + θpzp = 0 then |z| > 1.
Under construction
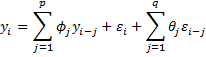
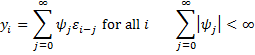
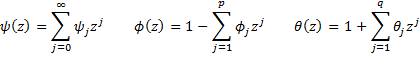
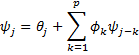
Hi,
After proving that a given ARMA process is weakly stationary, how can one proceed to obtain the mean and variance of the process?
How to obtain the mean and variance of an ARMA(p, q) process depends on the values of p and q.
1. When q = 0, then the mean is given by Property 1 of
https://real-statistics.com/time-series-analysis/autoregressive-processes/autoregressive-processes-basic-concepts/
2. When p = 1 and q = 0, then the variance is given by Property 2 of that same webpage.
When p = 2 and q = 0, then the variance is given by Property 7 of that same webpage.
3. As you can see from the following webpage, the mean for any ARMA(p,q) process is the same as that of an ARMA(p,0) process
https://real-statistics.com/time-series-analysis/arma-processes/arma-processes-basic-concepts/
4. See https://stats.stackexchange.com/questions/196994/arma-1-1-variance-calculation for the variance of an ARMA(1,1) process
See https://stats.stackexchange.com/questions/97274/variance-of-arma2-1 for the variance of an ARMA(2,1) process
These last two webpages, explain how to obtain the variances for other ARMA processes.
Charles
Do you provide a web page that explains your notation like, θ, φ, ψ, and so on? I took statistics decades ago and other than sigma, I don’t remember what the Greek letters signify.
Hi Charley,
Different authors use symbols in different ways, and so, while there are similarities, there are differences. I tend to use the symbols as described at
https://real-statistics.com/mathematical-notation/statistical-symbols/
Charles