Calculate ARMA(p,q) coefficients using maximum likelihood

We will assume an ARMA(p, q) process with zero mean

image237z

We will further assume that the random column vector Y = [y1 y2 ··· yn]T is normally distributed with pdf f(Y; β, σ2) where β = [φ1 ··· φp θ1 ··· θq]T. For any time series y1, y2, …, yn the likelihood function is

image238z

where Γn is the autocovariance matrix. As usual, we treat y1, y2, …, yn as fixed and seek estimates for β and σ2 that maximizes L, or equivalently the log of L, namely

image239z

This produces the maximum likelihood estimate (MLE) B, s2 for the parameters β, σ2. Equivalently, our goal is to minimize

image240z

Property 1: For large enough values of n, \sqrt {n}(B–β) is multivariate normally distributed with mean 0 and covariance matrix σ2 \Gamma_{p+q}^{-1}, i.e.

image241z

Observation: From Property 1, we can conclude that for large enough n, the following holds, where the parameter with a hat is the maximum likelihood estimate of the corresponding parameter.

AR(1) image242z
AR(2) image243z
MA(1) image244z
MA(2) image245z
ARMA(1,1) image246z

It turns out that -2LL can be expressed as

-2LL expression

Thus to minimize -2LL, we need to minimize

image248z

We show how to do this in Calculating ARMA Coefficients using Solver.

14 thoughts on “Calculate ARMA(p,q) coefficients using maximum likelihood”

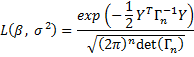
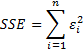
  1. Dear Charles,
    Will ARIMA be useful to apply in software project data to find out correlation among the employee skillset and availability so that we can take decision to assign the task.

    Reply

  2. Just for the clarity of things and consistency in notation you should use lower case “ln” for the natural logarithm below the box showing the distribution properties.

    Reply

  4. Dear Charles,

    If we arrive at the criterion of minimizing the squared residuals, why do people fuss so much about ‘maximizing likelihood’?

    Another question, is there a formula for the general terms in the autocovariance matrix for orders higher than AR(1)?

    Thanks,
    O.

    Reply

Leave a Comment