ARIMA Forecasting

The forecasting approach is exactly as described in Real Statistics ARMA Data Analysis Tool. The only difference now is that we need to account for the differencing.

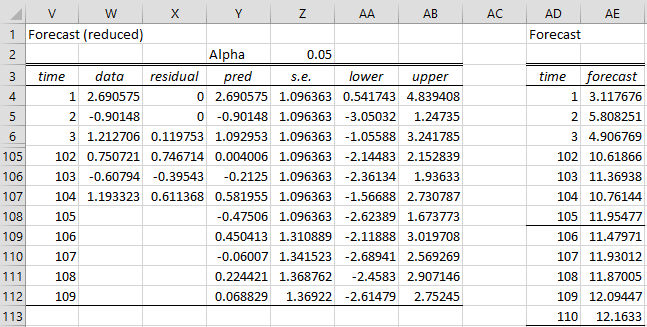
Example 1: Find the forecast for the next five terms in the time series from Example 1  of Real Statistics ARMA Data Analysis Tool based on the ARIMA(2,1,1) model without constant term.

Real Statistics ARIMA forecast

Figure 1 – Forecast for ARIMA(2,1,1) model

The table on the left side is calculated exactly as in Figure 3 of Real Statistics ARMA Data Analysis Tool. The right side undoes the differencing. E.g. Cell AD4 contains the formula =B4 (with reference to the data in Figure 1 of Calculating ARIMA Model Coefficients). Cell AD109 contains the formula =X108+AD108.

Note that if you had not assumed that there was no constant term, cell AD109 would contain the formula =X108+AD108+J$6. If Differences is 2, then AD109 would contain the formula =X107+2*AD108-AD107+J$6.

13 thoughts on “ARIMA Forecasting”

  1. Dear Dr. Zaiontz,

    If I wanted to run a SARIMAX model, would I do it just like how you did ARIMAX, except instead of using ARIMA, I would use SARIMA on the residuals of the linear regression analysis?

    Best regards,

    Crispus

    Reply

  3. Hi Charles,

    If i have removed the trend and seasonality in a model using quad + periodic dummies and used the resulting errors to build an ARIMA model which part of the model’s output should be considered to add back to the original errors? That is, forecast (reduced) table or forecast table.

    Thanks,
    Vijay

    Reply

  4. Hi, Charles!

    Most data I’ve been working with is non-stationary and has both trend and seasonal components. In this case, why (or when) should I use ARIMA models instead of Holt-Winter’s? It’s just a matter of accuracy comparision?

    Thank you!

    Reply

  5. Hi Charles,

    Predicting stock price data for intraday 1 minute candle. Data is stationary when d = 1, used your ARIMA tool.

    ADF Test

    criteria schwert
    drift yes
    trend yes
    lag 16
    alpha 0.05

    tau-stat -10.48182928
    tau-crit -3.42474216
    stationary yes
    aic 2.604432535
    bic 2.684661284
    lags 4

    As time increases by each 1 minute with new data, it is observed that
    AR Order 2
    MR Order 3,4,5,….20,22,
    Diff 1

    Question: What does it interpret when MR order increases more than 20, as your tool is restricted to 20. Do i need to change anything so that it works?

    Thanks,
    Venkat

    Reply

    • Venkat,
      Are you saying that you need an MA order larger than 20? The limit I am using is arbitrary, but it is hard-coded in the software. I can increase this limit in a future release. Let me know what limit makes sense to you.
      Charles

      Reply

      • Hi Charles,

        Yes, it would be great if you can increase the limit further or some other way which we can get the same results with less MA order using some transformations.

        Thanks,
        Venkat

        Reply

        • Venkat,
          20 seems like a pretty high value, but I will look into increasing it slightly. You should make sure that you really need more than 20.
          Charles

          Reply

          • Hi Charles,

            Yes, i need more than 20. Based on my experience with the data, i have observed that MA order has
            greater than 30 as well. Is it possible to fix the limit as 50 so that it can be usefull. May be this be can be edited in the future release which was hard coded.

            Thanks,
            Venkat

Leave a Comment