ARIMA Differencing

Basic Concepts

In order to create a stationary process, differencing may be necessary. For example, the graph of closing Dow Jones indices for October 2015 (see Example 1 of Stationary Process), as shown in Figure 1, clearly shows an increasing trend. Differencing is a way to eliminate such trends.

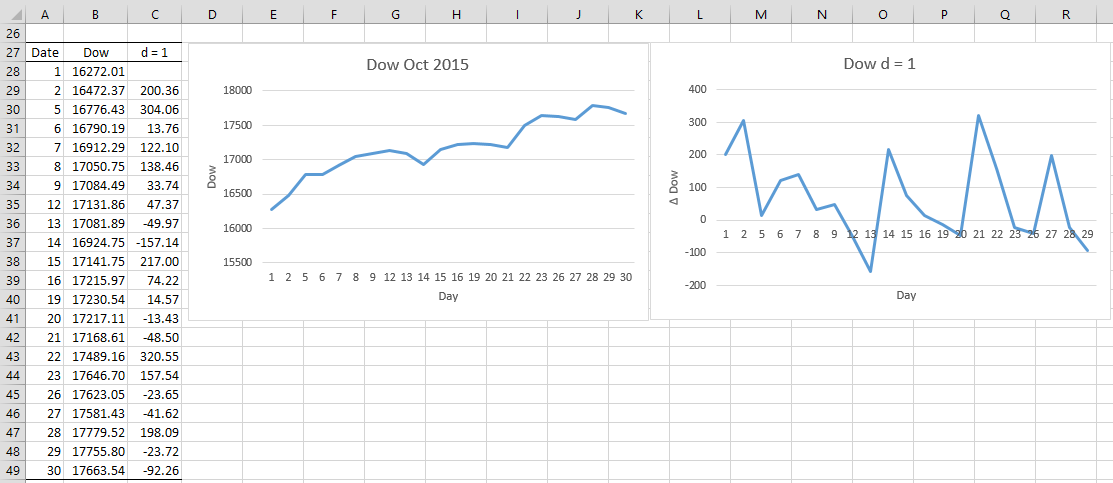
Figure 1 – Dow Jones Indices for October 2015

First-order differencing addresses linear trends, and employs the transformation z_i = y_i – y_i-1. Second-order differencing addresses quadratic trends and employs a first-order difference of a first-order difference, namely z_i = (y_i – y_i-1) – (y_i-1 – y_i-2), which is equivalent to z_i = y_i – 2y_i-1+ y_i-2.

Taking first-order differences for the data in Figure 1 results in the chart on the right. The trend seems to have been eliminated.

ARIMA

An autoregressive integrated moving average (ARIMA) process (aka a Box-Jenkins process) adds differencing to an ARMA process. An ARMA(p,q) process with d-order differencing is called an ARIMA(p.d,q) process. Thus, for example, an ARIMA(2,1,0) process is an AR(2) process with first-order differencing.

It is important not to over-difference since this can cause you to use an incorrect model. Some rules-of-thumb indicating that you may have differenced too many times are:

• The autocorrelation of a differenced series is less than -.5
• Differencing increases the variance

Rules-of-thumb

An AR(p) or MA(q) process has a unit root if the sum of the non-constant coefficients is 1.

Additional rules-of-thumb:

• If an AR(p) process has a unit root then the level of differencing should be increased
• If an MA(q) process has a unit root then the level of differencing should be decreased

Assume that column A contains a time series of size n starting in cell A1. Now suppose we want to place the 1^st order differences (of size n-1) in column B starting in cell B2, the 2^nd order differences (of size n-2) in column C starting in cell C3, and so on with the 7^th order differences (of size n-7) in column H starting in cell H8, then the formulas that need to be used in these starting cells are as follows:

• B2: A2-A1
• C3: A3-2*A2+A1
• D4: A4-3*A3+3*A2-A1
• E5: A5-4*A4+6*A3-4*A2+A1
• F6: A6-5*A5+10*A4-10*A3+5*A2-A1
• G7: A7-6*A6+15*A5-20*A4+15*A3-6*A2+A1
• H8: A8-7*A7+21*A6-35*A5+35*A4-21*A3+7*A2-A1

For each column, you need to highlight the range down to the nth cell in that column and press Ctrl-D to get the other values. Note that for the 7^th order difference, the coefficients used are C(7,0) = 1, C(7,1) = 7, C(7,2) = 21, etc.

Worksheet Function

Real Statistics Function: The Real Statistics Resource Pack provides the following array function.

ADIFF(R1, d) – takes the time series in the n × 1 range R1 and outputs an n–d × 1 range containing the data in R1 differenced d times

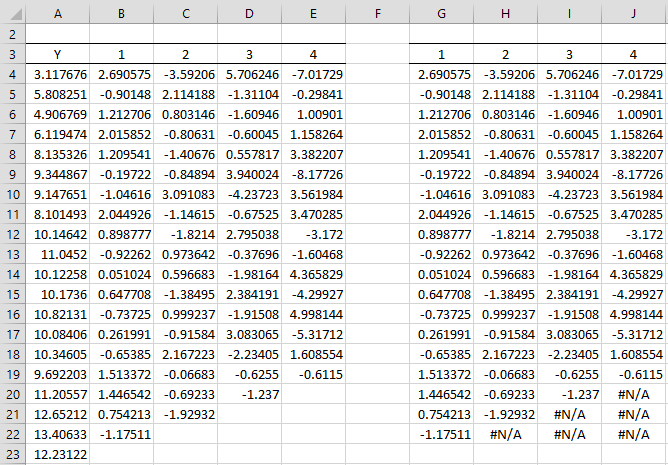
Example 1: Find the 1^st, 2^nd, 3^rd, and 4^th differences for the data in column A of Figure 1.

Figure 1 – Differencing

Here cell B4 contains the formula =A5-A4, cell C4 contains the formula =B5-B4 (or A6-2*A5+A4), cell D4 contains the formula =C5-C4 (or A7-3*A6+3*A5-A4) and cell E4 contains the formula =D5-D4 (or A8-4*A7+6*A6-4*A5+A4).

Range G4:G22 contains the array formula =ADIFF($A$4:$A$23,G3). If we highlight the range G4:J22 and press Ctrl-R, we get the result shown on the right side of Figure 1.

Examples Workbook

Click here to download the Excel workbook with the examples described on this webpage.

References

Nau, R. (2020) Identifying the order of differencing in an ARIMA model
https://people.duke.edu/~rnau/411arim2.htm