Transformations to Create Symmetry

Basic Concepts

When a sample is not normally distributed and is not even symmetric, then sometimes it can be useful to transform the data so that the transformed data is more normal or at least roughly symmetric. We touch upon the subject in Transformations, and we will explore this concept a little further here.

When data is skewed to the left, transformations such as f(x) = log x (either base 10 or base e) and f(x) = \sqrt{x} will tend to correct some of the skew since larger values are compressed. Neither of these transformations accept negative numbers, and so the transformations f(x) = log (x+a) or f(x) = \sqrt{x+a} may need to be used instead where a is a constant sufficiently large so that x + a is positive for all the data elements. 

Examples

Example 1: Determine whether a log transformation makes the data in Figure 1 more normally distributed.

Log-transformation data

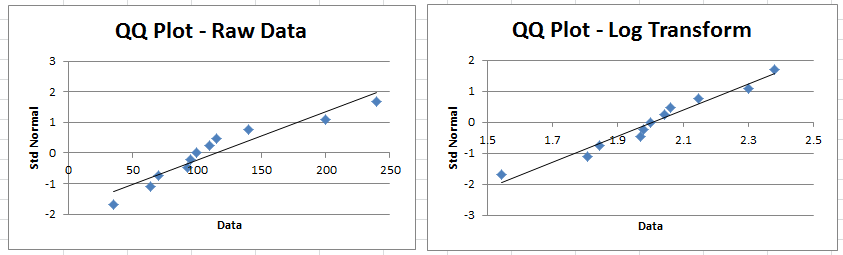
Figure 1 – Use of a log transformation to create symmetry

If we create a QQ Plot as described in Graphical Tests for Normality and Symmetry, we see that the data is not very normal (Figure 2). We now make a log transfer. We choose log base 10, although the result would be similar if we had chosen log base  (i.e. a natural log).

The QQ Plot (see Graphical Tests for Normality and Symmetry) shown on the left side of Figure 1 demonstrates that the data are not very normally distributed. We next consider a log transfer based on log base 10 (e.g. cell R4 contains the formula =LOG(R3)), although the result would be similar if we had used log base e (i.e. a natural log).

Log transformation QQ plots

Figure 2 – QQ plots of data before and after log transformation

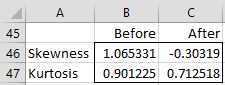
As can be seen from the chart on the right side of Figure 2, the transformed data is a little better fit for a normal distribution. Also notice the change in skewness and kurtosis (Figure 3), since the log-transformed data has values closer to what would be expected from a normal distribution (see Analysis of Skewness and Kurtosis).

Transformation skewness and kurtosis

Figure 3 – Skewness and kurtosis before and after the log transform

The Shapiro-Wilk test accepts both the raw data and log-transformed data as being normally distributed, although p-value = .23 for the raw data, but p-value = .87 for the transformed data.

More Information

See Box-Cox Transformation for a description of a commonly used method for normalizing data.

Examples Workbook

Click here to download the Excel workbook with the examples described on this webpage.

Reference

Feng, C., Wang, H., Lu, N., Chen, T., Hua, H., Lu, Y., Tu, X. (2014) Log-transformation and its implications for data analysis. Shanghai Arch. Psychiatry
https://www.ncbi.nlm.nih.gov/pmc/articles/PMC4120293/#:~:text=The%20log%20transformation%20is%2C%20arguably,normal%20or%20near%20normal%20distribution.

8 thoughts on “Transformations to Create Symmetry”

  1. Hi Charles
    thanks a lot for your help..
    plz i want to know if i have a histogram and Scatterplot graphs and I want to know from the shape if its normal or need a transformation to logt..so its enough to decide that from the shape only or I need to do something elsa is P value can help me in this case..
    by the way, I will continue with ANOVA also..
    thanks..

    Reply

    • Amal,
      If you create the histogram with enough detail, you should be able to tell whether the data is normally distributed or not. In any case, I suggest that you confirm this by using a statistical test: generally the Shapiro-Wilk test is the preferred test.
      I don’t think that a scatter graph would be very helpful.
      Charles

      Reply

  2. Hello Charles. Im trying to understand the whole concept of “normality” and how the data is transformed by some statistical tests.
    my question is: what is the best process to analyze normality and why? (symetrical and un-skewed gaussian distribution)

    ive been dealing with the KS test, AD test and Ryan Joiner test. Some teachers have told me that these tests tend to transform the data and i cant understand how and why they do that? Im working with samples (°C temp reading of several stations between rainy and non rainy season) that i need to check normality first (of rainy and non rainy season before testing for differences between the two seasons)

    Do you think that the analysis of skewness and Kurtosis is the best method to test gaussian distribution in a sample?

    Thanks for your webpage.

    Reply

  3. Hi Charles,

    Just wanted to say your thanks for the info provided on your site. This is at least the 3rd time I’ve used it to figure out something in stats. I’m working on my MS in Predictive Analytics, and some concepts are just plain tough to get.
    The textbooks in general circulation are often lacking in their accessability. It’s great when things are presented well in plain English. You are a good writer, and explain things well for those of trying to climb this sometimes rather steep learning curve.

    Again thanks for our site.

    Best regards,

    -John Ryle

    Reply

Leave a Comment