The following version of the Shapiro-Wilk Test handles samples between 12 and 5,000 elements, although samples of at least 20 elements are recommended. We also show how to handle samples with more than 5,000 elements. A modified version works for samples with 3 to 11 elements.
Basic Concepts
Assuming that the sample has n elements, perform the following steps:
1. Sort the data in ascending order x1 ≤ … ≤ xn
2. Define the values m1, …, mn by
mi = NORM.S.INV((i − .375)/(n + .25))
3. Let M = [mi] be the n × 1 column vector whose elements are these mi and let
If M is represented by the n × 1 range R1 in Excel, then =SUMSQ(R1) calculates the value m.
4. Set u = 1/ and define the coefficients a1, …, an where
ai = mi / for 2 < i < n − 1
a2 = −an-1 a1 = −an
It turns out that ai = −an-i+1 for all i and that
where A = [ai] is the n × 1 column vector whose elements are the ai.
5. The W statistic is now defined by
Because of the above properties of the coefficients a1, …, an it turns out that W = the square of the correlation coefficient between a1, …, an and x1, …, xn. Thus the values of W are always between 0 and 1.
It also turns out that for values of n between 12 and 5,000 the statistic ln (1−W) is approximately normally distributed with the following mean and standard deviation:
6. Thus we can test the statistic
using the standard normal distribution. If the p-value ≤ α then we reject the null hypothesis that the original data is normally distributed.
Examples
Example 1: Repeat Example 1 of Shapiro Wilk Original Test using the expanded test.
Figure 1 – Expanded Shapiro-Wilk Test
We carry out the calculations described above to get the results shown in Figure 1 (see Figure 2 for key formulas used). The W statistic is 0.971066. The p-value = .921649 > .05 = α shows that there are no grounds for rejecting the null hypothesis that the data are normally distributed.
Figure 2 – Key formulas from Figure 1
Worksheet Functions
Real Statistics Excel Functions: The Real Statistics Resource Pack contains the following functions.
SHAPIRO(R1) = the Shapiro-Wilk test statistic W for the data in R1 using the expanded method
SWTEST(R1) = p-value of the Shapiro-Wilk test on the data in R1 using the expanded method
SWCoeff(n, j) = the jth coefficient for samples of size n
SWCoeff(R1, C1) = the coefficient corresponding to cell C1 within the sorted array R1
SWPROB(n, W) = p-value for the Shapiro-Wilk test for a sample of size n and statistic W
Note that these functions can optionally take an additional argument roy, i.e. SHAPIRO(R1, roy), SWTEST(R1, roy), SWCoeff(n, j, roy) and SWCoeff(R1, C1, roy) and SWPROB(n, W, roy). When omitted this argument defaults to TRUE (i.e. the values for the expanded Shapiro-Wilk test as described above are used). If roy is set to FALSE then the values for the original Shapiro-Wilk test are used instead.
The SHAPIRO and SWTEST worksheet functions ignore all empty and non-numeric cells. The array or range R1 in SWCoeff(R1, C1) should not contain any empty or non-numeric cells.
Example
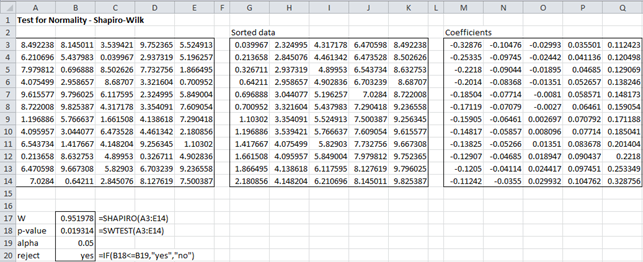
Example 2: Determine whether the data in range A3:E14 of Figure 3 is normally distributed using the Shapiro-Wilk test.
Figure 3 – SW Test using Real Statistics formulas
This time we use the Real Statistics functions described above to obtain the results shown in Figure 3. The value of W (cell B17) and the p-value (cell B18) shown in the figure are calculated using the formulas indicated. Since p-value = 0.019314 < .05 = α, we reject the hypothesis that the data are normally distributed. Note that we don’t need to sort the data and the data does not have to be arranged in a column to use the formulas.
If for some reason you want to obtain the coefficients, then you do need to sort the data. This can be done by highlighting the range G3:K14, entering =QSORT(A3:E14), and pressing Ctrl-Shft-Enter. The first coefficient is obtained by entering the formula =SWCoeff($G$3:$K$14,G3) in cell M3. When you highlight the range M3:Q14 and press Ctrl-R and Ctrl-D, all the coefficients will be displayed as shown in Figure 3.
Observations
If the sample is larger than 5,000, then you can randomly divide the sample into a number of approximately equal-sized smaller samples and then run the SW algorithm as described above on each sample to obtain the z score for each of the smaller samples. Suppose there are k such samples with z scores of z1, …, zk. Recall that if range R1 contains sample i, then zi = NORM.S.INV(SWTEST(R1)).
The average of the z-scores is an approximation of the z value for the whole sample. The expected mean of z is the average of the means of the zi, namely 0/k = 0, and the standard deviation of z should be the standard deviation of the zi divided by √k, namely 1/. Thus, z ∼ N(0, 1/k) and so you can test z
using the standard normal distribution.
Data Analysis Tool
Real Analysis Data Analysis Tool: The Descriptive Statistics and Normality data analysis tool in the Real Statistics Resource Pack has a Shapiro-Wilk option. You can use this option to perform the Royston version of the SW Test, as described in Example 3.
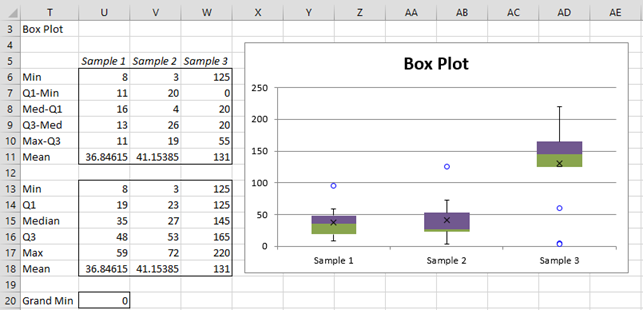
Example 3: Determine which of the three samples displayed on the left side (range A3:C16) of Figure 4 is normally distributed.
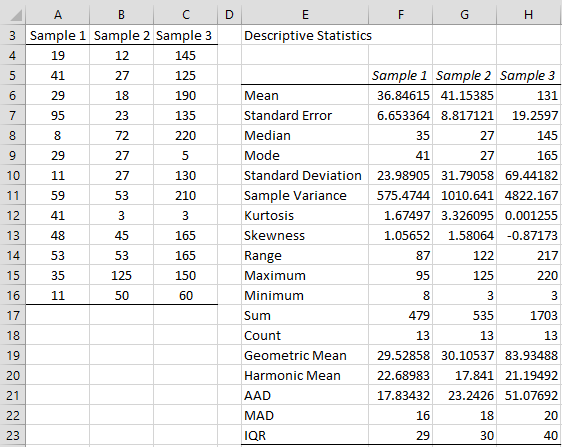
Figure 4 – Descriptive Statistics and Normality (part 1)
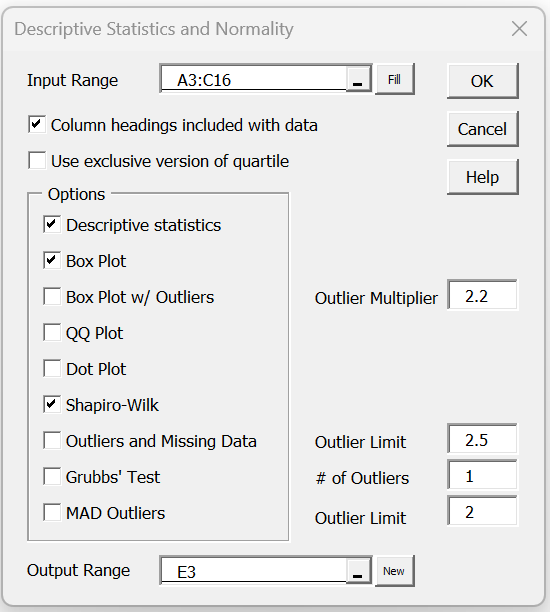
Enter Ctrl-m and select the Descriptive Statistics and Normality tool from the dialog box that appears (or from the Desc tab if using the multipage user interface). The dialog box displayed in Figure 5 now appears. Choose the Descriptive Statistics, Box Plot and Shapiro-Wilk options as shown and click on the OK button.
Figure 5 – Dialog box for Descriptive Statistics and Normality
Output
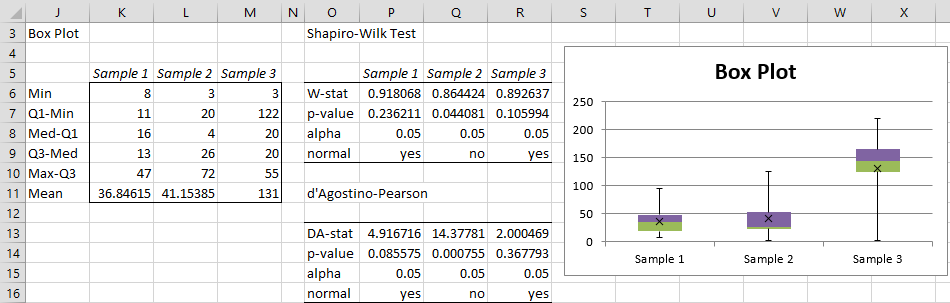
The resulting output is shown on the right side of Figure 4 and in Figure 6. As we can see, based on the Shapiro-Wilk test only Sample 2 shows a significant departure from normality (p-value = 0.044 < .05 = α).
Figure 6 – Descriptive Statistics and Normality (part 2)
This conclusion is supported by the fact that the kurtosis for Sample 2 is high (3.326) and the fact that the Box Plot for Sample 2 is not very symmetric.
Note that choosing the Shapiro-Wilk option also displays the d’Agostino-Pearson test, as shown in Figure 6 and described in d’Agostino-Pearson Test.
Box plot with outliers
Note that if we use the Box Plot with Outliers option in Figure 5, we get the chart shown in Figure 7. There we see that each of the samples has one or more potential outliers and despite these outliers Sample 1 and 3 appear to be normally distributed. The potential outlier for Sample 2 (the data value 125) appears to distort that sample away from normality. In fact, if we remove 125 from the sample, the SW test would show that the data likely comes from a normally distributed population (W = .95 and p-value = .68).
Figure 7 – Box Plot with Outliers
Examples Workbook
Click here to download the Excel workbook with the examples described on this webpage.
Reference
Royston, J. P. (1992) Approximating the Shapiro-Wilk W-test for non-normality, Statistics and Computing, vol. 2, pp. 117-119.
http://dx.doi.org/10.1007/BF01891203


This is lovely! Such a clear explanation and with the source literature too. Actually it was the only completely comprehensible exposition I could find. I am so looking for an opportunity to put this test into action. Thank you very much.
Glad I could help, David.
Charles
Thank you for this tool!
I have a rather big sample (about 2,000 data points) – with some missing values. In your description it says that the Shapiro-Wilk calculation just ignorse empty boxes/missing values, so that these are not a problem and do not have to be manually deleted before applying the test via your toolbox. Does this also apply to the descriptive statistics output, especially the median?
Thank you!
Despina
Hello Despina,
I believe that it does apply to the Descriptive Statistics output too.
Charles
when I perform the shapiro wilks test on my samples.
1) manually vs the plugin. I get similar results, is it normal?
2. Is there a way to calculate the p-value manually?
Greetings from Lima-Peru
Hello Miguel,
1. Perhaps I am not understanding your assertion, but you should bet similar results when you perform the SW test manually vs. the plugin (presumably the data analysis tool or worksheet function).
2. This webpage describes how to calculate the p-value manually.
Charles
Hello Charles.
Thank you for providing this extended HAND-CRANKED method of conducting the Wilks-Shapiro Test for Normality, with n = 12 observations. I use EXCEL and I always try to understand the arithmetic behind the madness. I won’t even ask about the terms and factors that were used to calculate the a(n-1) and a(n) values. I will just take it at face value that they are the words (or calculations) of the statistical gods and I will accept them as such. Same thing for the mean and the standard deviation values. I do have one question though. My Z0 score came out to be -1.416, just as yours did, but I don’t understand why you calculated the P-value as 1 – normsdist value instead of just using the normdist value of 0.07835?
Am I missing something very simple or is there a different way I am supposed to calculate the P value?
I will look forward to your response.
v/r
Kenneth Lewis
Hi Kenneth,
I don’t know why the p-value was calculated in this way. Note that 1-NORMSDIST(W) is equal to NORMSDIST(-W). Thus, the test could have used -W in place of W, in which case NORMSDIST(W) could have been used.
Charles
Thank you Charles.
v/r
Kenneth Lewis
is it NORMSDIST(-W) or NORMSDIST(-Z) ? Thank you sir
Hello Adi,
If I understand your question correctly, the answer is =NORMSDIST(-Z)
Charles
Dear Charles,
I found this link and I think i can ask you the questions here straightaway instead of emailing you.
Firstly, in figure 1 what are the inputs and the outputs calculated in this table
Secondly, after replicating figure 1 with the help of figure 2 formulas, then I had to check if the data is normally distributed in here should I continue doing example 2 which is calculating the coefficients using =SWcoeff of Figure 1 data set only and then do example 3 with one sample instead 3 (like you’ve done it)??
I really appreciate your help as I’m so confused and thanks in advance.
Hello Ethan,
In Figure 1, the input is shown in column S and the output in column Y. The data in column S comes from a similar example on the webpage referenced (you can click on the link).
You can perform the test by using the formula SWTEST, but the easiest way is to use the data analysis tool as described in Example 3.
Charles
Hi Charles,
I am trying to calculate the degrees of freedom for my Shapiro-Wilk calculations. Do you know of a way to do this?
Thanks!
The test uses the standard normal distribution which does not have any degrees of freedom.
Charles
Hey Charles,
Thank you for the detailed calculations on the Shapiro-Wilk (S-W) Expanded Test .
I have an observation regarding comparability of expanded version of S-W and the Ryan-Joiner tests for Normality.
I have read from Ryan & Joiner’s 1976 article on ‘Normal Probability Plots and Tests for Normality’ that statistics, Rp and W agree to 3 decimal places.
But when I recreate ‘W’ using your calculations in Excel and compare the results from Minitab’s ‘RJ’ (Minitab calls Rp value as RJ), the variation is larger than expected. For ‘p-values’ that are around the range of 0.01 to 0.1 (for either S-W or R-J), I find that some data sets are considered ‘Normal’ by R-J and not by S-W and vice-versa.
I was trying to validate the Shapiro-Wilk results on a data set from a program output using the Ryan-Joiner normality test from Minitab, but could not co-relate the results. On the other hand, the program output perfectly matches the output using your calculations.
Amar S Jyotinagaram R
Charles hello!
One question, if I have a data set n=60 and I perform the test using Real Statistics pack and just using Excel formulas as stated in the Example 1. above shouldn’t I get the same solution both ways in regards to testing the normality distribution?
Thank you in advance,
Sara
Sara,
When you say “both ways” do you mean that the p-value obtained by the original version of the test will be equal to the Royston version of the test? In any case these results will be similar but not the same. In any case the original approach does not support samples of size n = 60 (the limit for the original approach is n = 50).
Charles
Hi Charles,
When I use the Royston approximating you mention above I get negative amounts instead of positive numbers in SW table. [ n=1 to 50. table a(1)-a(25) ]
Do you have any idea?
Thanks,
a(i) = m(i)/sqrt(eps)
1. I assume sqrt(eps) is positive.
2. SW table contains only the first half – m(1) to m(n/2): which are on the left side of the normal distribution, so must be negative
3. positive/negative => Negative
example for n=6:
i=3 => (i-0.375)/(n+0.25)=(3-0.75)/(6+0.25)=0.42
m(3)=NORM.S.INV(0.42)=-0.20189
Method: a(1), a(2), a(3)
Shapiro-Wilks: 0.6431, 0.2806, 0.0875
Approximating: -0.64397, -0.28071, -0.08825
Oren,
Yes, I just checked and the coefficients using the Royston version of the test are the negative of those using the original version. E.g.
data coeff
34 -0.605060857
56 -0.316302802
78 -0.175109665
99 -0.056484528
111 0.056484528
189 0.175109665
211 0.316302802
290 0.605060857
Here the first coefficient (in cell B2) is calculated using the formula =SWCoeff($A$2:$A$9,A2), assuming that the data is in range A2:A9 and the coefficients are in range B2:B9
Charles
Dear Charles,
First I want to say that you have an amazing site, I have no words to describe the superb content. Thank you Charles 🙂
I tried to calculate the coefficients a(1), …, a(n) {actually we use only a(1),…, a (n/2)}
a(n) is positive.
Did you write above that a1=-a(n), which say a(1) is negative?
Also a(i)=m(i)/sqrt(eps) is negative.
But in the Shapiro-Wilk Tables, I can see all a(i) values are positive?
Another question, the approximating support slightly difference results.
For example for n=6: a(1), a(2), a(3)
Shapiro-Wilks: (0.6431, 0.2806, 0.0875
Approximating: ( -0.64397, -0.28071, -0.08825)
What a(i) values is better to use for i=1 to 50?
I understand that Shapiro-Wilks values are also not accurate.
Is the approximating you describe above more accurate the original Shapiro-Wilks values?
Thanks
Oren,
1. a(1) = -a(n) doesn’t mean that a(1) is negative. E.g. if a(n) is -0.3, then a(1) is 0.3, which is positive. In any case, half the coefficients are positive and the other half are the negative of the positive values.
2. When you say approximate value, then I assume that you are referring to the Royston approximation. Probably the original Shapiro-Wilk values are more accurate for values in the table.
Charles
Hey Charles,
Could the expanded Shapiro-Wilk test also be applicable to less than 12 samples? Or do I have to apply the original Shapiro-Wilk test?
Please let me know! Thanks.
David, the expanded Shapiro-Wilk test is applicable to less than 12 samples. It requires a minimum of 3 elements.
Charles
Hi Charles,
but why do you state at the beginning that you need sample sizes of 12 up to 5000 and even recommend at least 20 elements ? What’s the reason behind that?
Thank you in advance.
Jürgen
It just means that the results will be more accurate with at lease 20 elements. You can use the algorithm if the sample contains at least 12 elements. Actually a modified version works for 3 to 11 elements. The Real Statistics functions list work for 3 to 5,000 elements.
Charles
Hello Charles,
First thanks a lot for this very clear and helpful document! I just had a question, if I wanted to check whether my data follows a log-normal law, which formulas would I have to change? I was wondering if it would work by just taking the log of my datas and then applying the same formulas as before… Thanks in advance for your reply!
Fiona,
Yes, that approach should work fine.
Charles
Thanks for the quick reply Charles!
Hello,
I am working with radar data that was taken to analyse flooding. I use GIS to determine water flow and accumulation. I have made a histogram and QQ plot of the radar elevations using GIS, and elevations are not normally distributed. The graphics are great, but I also need statistics to show the abnormal distribution. The radar data contains 9,853,404 elevation points. How can I use stats to show the elevations values are not normally distributed?
Jackie,
You can use the Shapiro-Wilk test as described on the referenced webpage.
Charles
Hi Charles,
Thank you for your time addressing the comments posted on here. It is much appreciated.
I have managed to expand a spreadsheet to hold and statistically analyse up to 5000 data points(from 200), though I still cant get the w-test to calculate correctly. Are you able to help or are you able to put in my touch with someone who can? I believe it would be a simple fix but I am baffled.
Eliza,
If you send me an Excel file with your data and analysis, I will try figure out what is going wrong.
You can find my email address at Contact Us.
Charles
Thank you so much Charles.
I am sending through an email now.
Hi!
First of all, thanks for your work. I’ve used your webpage several times to understand some statistics.
I have one doubt here, the .375 and .25 numbers used in “mi = NORMSINV((i − .375)/(n + .25))” are totally independent of the data?
I have a problem with that argument because my data has negative values, so excel can’t return anything in that formula, given that I’m entering a negative probability.
Could you help me with that? Thank you!
Alvaro,
If your data values are say -3, 7, 10, -1, -5, then then data needs to be arranged in increasing order as -5, -3, -1, 7, 10.
When calculating mi, it is important to note that i is not the data value but its index. Thus -5 corresponds to 1, -3 corresponds to 2, etc. These indices are all positive integers.
Charles
Thank you so much! I was using the actual data, instead of the index. My fault.
I am looking for a version of the Shapiro & Wilk tables (coefficients and p-values) that I can easil paste in to my spreadshhet. Thanks, Kevin.
Kevin,
You might want to use the version described on the following webpage:
https://real-statistics.com/tests-normality-and-symmetry/statistical-tests-normality-symmetry/shapiro-wilk-test/
You can use the version on the examples workbook, which you can download for free.
Charles
I would like to thank you for all the support I found here during the development of my final work (I’m student yet). Never stop your work, it’s very helpful and you write clear and understandable.
Regards,
André Vendramini
Thank you very much André for your support. I am glad that you found the website helpful.
Charles
Dear Charles
Thank you for a very useful add-on. However when I try to use e.g. a test for normality I get an error message: Compile error in hidden module: Analysis. I get an error when I use any of the functions.
Can you help?
Many thanks
Philip
Dear Philip,
In order to help you I need some additional information, namely:
1. Does the function =VER() work? If not, then you probably haven’t installed the software as indicated on the website. When you press Alt-TI you should see RealStats in the list that is displayed with a check mark next to it. If not, you need to click on the Browse button and locate where you have stored the file containing the Real Statistics add-in that you downloaded from the website.
2. If this is not the problem, then please tell me what is displayed when you use the =VER() function and what release of Excel you are using (Excel 2007, Excel 2010, etc.).
Charles
Hello Charles,
I find your website very interesting. Thank you.
When trying to follow your lead, I encounter that I would have used =NORMDIST(z;mu;sigma;1). If I just write =NORMDIST() I assume that it is a N(0,1) which is not the case but that’s the way I obtain your p-value.
What am I misunderstanding?
Thank you very much
Gaussiano,
The formula =NORMDIST() is not valid and will result in an error. I used =NORMSDIST(x) which is N(0,1).
Charles
Hi Dr. Zaiontz,
By chance do you have a reference on where the values for an and an-1 came from:
a_n=-2.706056u^5+4.434685u^4-2.071190u^3-0.147981u^2+0.221157u+m_n m^(-0.5)
a_(n-1)=〖-3.582633u〗^5+〖5.682633u〗^4 〖-1.752461u〗^3+〖-0.293762u〗^2+0.042981u+m_(n-1) m^(-0.5)
Thank you so much
RobS
Hi RobS,
The reference is Royston’s paper. See Bibliography for details.
Charles
i am struggling on how to interpolate the data .can someone please help me and show me the clear formula.because I know how to calculate the value of W .
If you are using the expanded version version of the SW test, you shouldn’t need to interpolate. If you are using the original SW test, then you might indeed need to interpolate, although the Real Statistics function will do this for you. In any case, to get more information about how to interpolate see the webpage https://real-statistics.com/excel-capabilities/table-lookup/.
Charles
Sir Charles,
Thank you for this tool. It will help me a lot in my research. All credits to you sir. This will significantly reduce my computations.
Again, thanks a lot. More power to you sir.
Jem
Hello – I also appreciate your excellent instruction. However using =SHAPIRO(R1,TRUE) [ver 3.5.1] for the data in in Figure 1 – Expanded Shapiro-Wilk Test, I’m unable to duplicate the W of 0.971066 worked out in that table. I get W = 0.9711225. Could you please show me my error? Thanks again for this resource!
Wade,
Thanks very much for your comment. It turns out that there is an error in the =SHAPIRO(R1,TRUE) formula. The value for W of 0.971066 is correct. In the calculation of the an coefficient I used 0.22157u instead of 0.221157u. As you can see the difference is quite small, but in any case I will correct this error in the next release of the software.
Charles
Wade,
I have now corrected the error in the Shapiro-Wilk capabilities. This is included in the latest release of the Real Statistics Resource Pack, Release 3.6.1, which was issued today.
Charles
Thanks a lot, for your wonderful site. This is really the best site, I know of, to lean statistics from basics. at the same time, your addin is too good. Congratulations for painstakingly carrying out this great service !
Two, inquiries:
1. Here, I am not able to find out the equation for the calculation of p-value.
2. In my laptop I could use the add in, but in office computer (windows 7, MSoffice 2007), I am not able to use your addin, the message comes is as follows: “can’t find project or library” in a visual basic windows. Can you please help !
Once again, I express my sincerest thanks, Sir. Regards!
1. The formula for the p-value is =1-NORMSDIST(Y12) (see Figure 1 and 2)
2. Which version of Excel are you using on your office computer? Is it the same version of Excel as you are using on your laptop?
Charles
Hey Charles,
I’d like to perform a Shapiro-Wilk expanded test with correction for ties as suggested by Royston (1989). It bassically implies adding the Sheppard correction to the sum of squares about the mean: -(n-1)h²/12. Can you give me a hint how to realise this with your Real Statistics Resource Pack? What makes it even more complicated is that grouping intervals are of unequal size.
All best
Philippe
Philippe,
I am not familiar with this correction factor for ties in the SW test and so don’t have any suggestions for how to do this with the Real Statistics software.
Charles
Hi Charles,
Thanks, I am trying to do this in excel and really appreciate your website. I have some question regarding to formulas.
W: I can not get the value as your excel :0.97XXX, it looks like the formula is wrong. Not sure if current formula of fig 2 is correct.
P value: can I know where I can find putt he formula?
thanks,
Kim
Kim,
I just checked all the formulas in Figure 2 and they seem correct. Which cells do you think have the wrong formulas, and what do you think is the correct formula (or why do you think the formula for W is wrong)? I don’t understand your question about the p value.
Charles
Suppose i have a values of W= 0.96, W=0.87, W=0.92, W=0.91 and sample of 80 for my ECG data what could be the P value for each W?? Kindly let me the P value by using the Extended shapiro test..
The p-value is calculated from W using the fact that ln(1-W) is approximately normally distributed with mean and standard deviation as given on the referenced webpage just before Example 1. From this fact you should be able to calculate the p-values using NORM.DIST, NORM.S.DIST, NORMDIST or NORMSDIST.
Charles