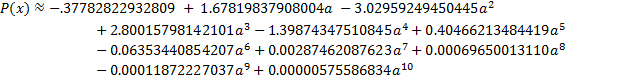Lilliefors distribution approximation
The following polynomial function provides an approximation, accurate to about two decimals places, for the Lilliefors distribution.
where ![]()
![]()
![]()
Worksheet Functions
Real Statistics Functions: The following functions are provided in the Real Statistics Resource Pack to implement the approximation of the Lilliefors distribution:
LDIST(x, n) = the p-value of the Lilliefors distribution at x for samples of size n
LINV(p, n, iter) = the critical value of the Lilliefors distribution at p for samples of size n; i.e. LINV(p, n, iter) = x where LDIST(x, n) = p, based on iter iterations (default 40)
For Example 2 of Kolmogorov Test for Normality, p-value = LDIST(0.184, 15) = .180996, which is similar to the estimate from LPROB(0.184, 15) = .182858. Similarly, Dn,α = LINV(.05, 15) = .218698 is similar to the estimate from LCRIT(15, .05, 2) = .2196.
LTEST function
The following function is provided in the Real Statistics Resource Pack to calculate the value of the Kolmogorov-Smirnov statistic Dn
LTEST(R1) = Dn for the data in range R1
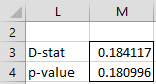
For Example 2 of Kolmogorov Test for Normality, referring to Figure 4 of Kolmogorov Test for Normality, LTEST(B4:B18) = .184117 (same as cell H20).
In fact, LTEST can be used as an array function which outputs a 2 × 1 column range containing and p-value (based on the LDIST approximation). The array function LTEST takes an optional second argument lab (default FALSE). When lab = TRUE then a column of labels is appended to the output.
Thus, referring to the input range in Figure 4 of Kolmogorov Test for Normality, the output from LTEST(B4:B18,TRUE) is as shown in Figure 1.
Figure 1 – Lilliefors Test
Examples Workbook
Click here to download the Excel workbook with the examples described on this webpage.
Reference
Lilliefors, H. W. (1967) On the Kolmogorov-Smirnov Test for Normality with Mean and Variance Unknown, Journal of the American Statistical Association, Vol. 62, No. 318, pp. 399-402.
https://pdfs.semanticscholar.org/4aad/1756e88dba86399a75891895e00b160f5460.pdf