Kolmogorov Distribution

Basic Concepts

For n sufficiently large, the values of Dn,α (two-tailed) (see Kolmogorov-Smirnov Test) are approximately equal to the inverse of the Kolmogorov distribution divided by the square root of n. This holds even for values of α not found in the Kolmogorov-Smirnov Table.  The cdf of the Kolmogorov distribution has the value

image7297

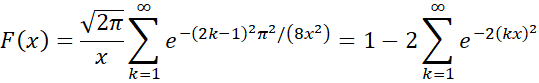
For sufficiently large n, \sqrt{n}Dn,α approximately follows the Kolmogorov distribution.

Furthermore, for any value of n, the critical value Dn,α  is approximately equal to

Critical value

where Dα is the critical value of the Kolmogorov distribution. E.g. for α = .05,  (i.e. F(1.3581) = .95 where F(x) is the cdf of the Kolmogorov distribution, as described above. Thus, for example

Critical value example

Worksheet Functions

Real Statistics Functions: The Real Statistics Resource Pack supplies the following functions:

KDIST(x, iter) = the value of the Kolmogorov distribution function F(x) where iter = the # of iterations used in calculating the infinite sum (default = 50).

KINV(p, iter0, iter) = the inverse of KDIST; i.e. KINV(p, iter) = x where 1 − KDIST(x, iter) = p. The inverse function is calculated from KDIST using iter0 iterations (default 40).

x takes values between 1.0 and 2.4 and p takes values between 0.0000198590086116779 and 0.269999671677355.

Observation: Based on the previous observation, for n sufficiently large, Dn,α = KINV(α)/SQRT(n), which yields the same result as the last line in the Kolmogorov-Smirnov Table (although with greater accuracy), and so 

Dn,α = KINV(α)/(SQRT(n)+.12+.11/SQRT(n))

More Worksheet Functions

To avoid having to handle the SQRT(n) terms in the above expression, you can instead use the following Real Statistics functions for samples that are sufficiently large:

Real Statistics Functions: The Real Statistics Resource Pack supplies the following functions:

KSDIST(x, n) = the p-value of the one-sample Kolmogorov-Smirnov test at x for samples of size n

KSINV(p, n) = the critical value at p of the one-sample Kolmogorov-Smirnov test for samples of size n

Actually, the first of these functions takes the form KSDIST(x, n, b, iter) and the second takes the form KSINV(p, n, b, iter0, iter), where

KSDIST(x, n, , TRUE, iter) = 1-KDIST(x*(SQRT(n) +0.12+0.11/SQRT(n)), iter)

KSDIST(x, n, , FALSE, iter) = 1-KDIST(x*SQRT(n), iter)

KSINV(p, n, , TRUE, iter0, iter) = KINV(p, iter0, iter)/(SQRT(n)+.12+.11/SQRT(n))

KSINV(p, n, , FALSE, iter0, iter) = KINV(p, iter0, iter)/SQRT(n)

b = TRUE (default) works better for small values of n, but when b = FALSE then it is assumed that n is sufficiently large so that the approximation described previously is sufficient. Note that the third argument in the above functions is used for the two-sample Kolmogorov-Smirnov test.

Observations

For Example 1 of Kolmogorov-Smirnov Test, where the sample size n = 1,000, we have

D1000,.05 = KSINV(.05, 1000) = KINV(.05)/(SQRT(1000)+.12+.11/SQRT(1000)) = .04278

which is pretty close to the value shown in cell G16 of Figure 3 of Kolmogorov-Smirnov Test. Referring to this figure, we can also calculate the p-value as follows:

p-value = KSDIST(G15,B14) = 1–KDIST(0.011706*SQRT(1000)) = .999167

Note too that D10,.05 = KSINV(.05, 10) = .4094 which yields the value calculated above via the formula =KINV(.05)/(SQRT(10)+.12+.11/SQRT(10)).

Reference

Ferguson, T. (2008) The Kolmogorov distribution
No longer available online

Wicklin, R. (2020) Kolmogorov D distribution and exact critical values
https://blogs.sas.com/content/iml/2020/06/24/kolmogorov-d-distribution-exact.html

Dimitrova, D. S., Kaishev, V. K. and Tan, S. (2017). Computing the Kolmogorov-
Smirnov distribution when the underlying cdf is purely discrete, mixed or continuous
https://www.jstatsoft.org/article/view/v095i10

18 thoughts on “Kolmogorov Distribution”

  1. Hi Charles
    I need a favour from your side..
    I have to compare two dataset of different Metrices(don’t have common metrices) to find out the common metric among them. But i am not able to do that.Please help me to do that

    Reply

  2. Dear Charles,

    first my thanks for your very useful work and great helpfulness.
    I have one small request: Since many of your functions are approximations, it would be very helpful if you could provide, alongside the definition, an indiction of the set of arguments over which they are valid. As an example, I have been plotting the KDIST function to understand it better, and found that it explodes below x = 0.05 (while it behaves just fine for x > 0.05). I suppose KDIST was not meant to be used for such small arguments, but there is no indication of this on the site.
    Similarly, since the set of images of KINV is [1;2.4], the relationship “KINV(p, m) = x where 1 − KDIST(x, m) = p” holds only for x in [1;2.4]; outside this interval the expression KINV(1-KDIST(x)) returns nonsensical results. Turning this around, the expression “1-KDIST(KINV(p))” only works correctly for p in [0;0.27], which leads me to the conclusion that KINV should indeed only be used for arguments smaller than 0.27 (i.e. the inverse for the left branch of the distribution function is not modeled) – but again I have found no indication of this on the site.
    Thanks!

    Reply

  3. Hi Charles, I’m triying to emulate a function to calculate this distribution based on the result you have mention (KSDIST(G15,B14) = 1-KDIST(G15*SQRT(1000)) = .999167.)
    nevertheless I’m getting a quite different value when using my function.

    could you help me known what I’m doing wrong?

    Public Function KSDIST(x As Variant, Optional n = 1000) As Variant
    Dim check As Boolean
    Dim t As Variant
    t = Sqr(8)
    check = False
    If x <= 0 Then
    check = True
    Else
    Dim F As Variant, k As Variant, R As Variant
    F = 0
    R = Application.SqrtPi(2) / x
    For k = 1 To n Step 1
    F = F + (1 / (Exp((2 * k – 1) * Pi) / (t * x)) ^ 2)
    Next k
    KSDIST = R * F
    End If
    If check = True Then
    MsgBox "x must be a positive number"
    Exit Function
    End If

    End Function

    Result KSDIS(0.011706,1000)=234.7407 🙁

    Reply

      • I found a different definition of Kolmogorov distribution when searching in google but in russian.

        Coul you please tellme if this function is equivalent to the one you used?

        Public Function KSDIST(x As Variant, Optional n As Variant = 1000) As Variant
        ‘Function that provides either KS Distribution p value or ks distribution value at x
        Dim F As Variant, i As Variant, y As Variant, R As Variant
        F = 0
        For i = -n To n Step 1
        F = F + (-1) ^ i * Exp((-2 * (i * x) ^ 2))
        Next i
        KSDIST = F
        End Function

        Reply

  4. Hi Charles

    How would I calculate the K-S D statistic against the random (Poisson) distribution, compare calculated D with Dα=0.05, and claim if the point pattern is clustered or not

    Thank you

    Reply

  5. Hi Charles – I was looking to build my own KS distribution without the use of the KSDIST and KSINV function. Would you have a quick guide on how to code it in excel or a formula?

    Reply

    • Hi Doc,
      You just need to program the formula given on the referenced webpage. Since it is an infinite sum, you will need to make a finite approximation.
      Charles

      Reply

Leave a Comment