Kolmogorov-Smirnov Test for Normality

Hypothesis Testing

Definition 1: Let x1,…,xn be an ordered sample with x1 ≤ … ≤ xn and define Sn(x) as follows:

image3572

Now suppose that the sample comes from a population with cumulative distribution function F(x) and define Dn as follows:

image3574

Observation: It can be shown that Dn doesn’t depend on F. Since Sn(x) depends on the sample chosen, Dn is a random variable. Our objective is to use Dn as a way of estimating F(x).

Critical Values

The distribution of Dn can be calculated (see Kolmogorov Distribution), but for our purposes now the important aspect of this distribution is the table of critical values. These can be found in the Kolmogorov-Smirnov Table.

If Dn,α is the critical value from the table, then P(Dn ≤ Dn,α) = 1 – α. Dn can be used to test the hypothesis that a random sample came from a population with a specific distribution function F(x). If

image3579

then the sample data is a good fit with F(x).

Confidence Interval

Also from the definition of Dn given above, it follows that

KS Dn part 1KS Dn part 2

KS Dn part 3

Thus Sn(x) ± Dn,α provides a confidence interval for F(x)

Examples (Frequency Table)

Example 1: Determine whether the data represented in the following frequency table is normally distributed where x represents rainfall amounts.

Frequency table KS test

Figure 1 – Frequency table for Example 1

This means that 8 elements have an x value less than 100 (i.e. between 0 and 100), 25 elements have an x value between 101 and 200, etc. We need to find the mean and standard deviation of this data. Since this is a frequency table, we can’t simply use Excel’s AVERAGE and STDEV.S functions. Instead, we first use the midpoints of each interval and then use an approach similar to that described in Frequency Tables as shown in Figure 2:

Frequency table mean variance

Figure 2 – Calculating mean and standard deviation

Thus, the mean is 481.4 and the standard deviation is 155.2.

Set-up for KS Test

We can now build the table that allows us to carry out the KS test, as shown in Figure 3.

Kolmogorov-Smirnov test Excel

Figure 3 – Kolmogorov-Smirnov test for Example 1

Columns A and B contain the data from the original frequency table. Column C contains the corresponding cumulative frequency values and column D simply divides these values by the sample size (n = 1000) to yield the cumulative distribution function Sn(x)

Column E uses the mean and standard deviation calculated previously to standardize the values of x from column A. E.g. the formula in cell E4 is =STANDARDIZE(A4,N$5,N$10), where cell N5 contains the mean and cell N10 contains the standard deviation (from Figure 2). Column F uses these standardized values to calculate the cumulative distribution function values assuming that the original data is normally distributed. E.g. cell F4 contains the formula =NORM.S.DIST(E4,TRUE). Finally, column G contains the absolute values of the differences between the values in columns D and F. E.g. cell G4 contains the formula =ABS(F4—D4). If the original data is normally distributed these differences will be zero.

Test Results

Now Dn = the largest value in column G, i.e. MAX(G4:G13) = 0.0117 (cell G8). If the data is normally distributed then the critical value Dn,α will be larger than Dn. From the Kolmogorov-Smirnov Table we see that

Dn,α = D1000,.05 = 1.36 / SQRT(1000) = 0.043007

Since Dn = 0.0117 < 0.043007 = Dn,α, we conclude that the data is a good fit for the normal distribution.

Example (Raw Data)

Example 2: Using the KS test, determine whether the data in Example 1 of Graphical Tests for Normality and Symmetry is normally distributed.

We follow the same procedure as in the previous example to obtain the results shown in Figure 4. Since the frequencies are all 1, this example might be a little easier to understand.

KS test in Excel

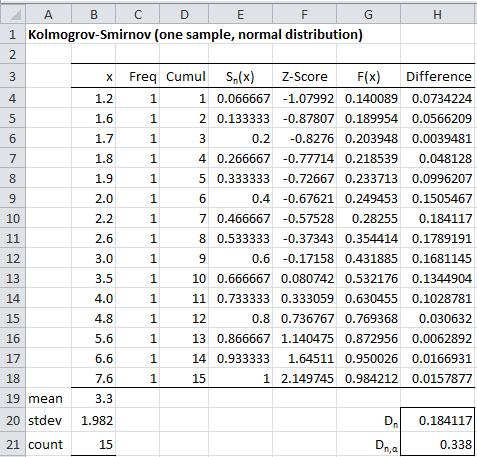
Figure 4 – KS test for data from Example 2

The Kolmogorov-Smirnov Table shows that the critical value Dn,α = D15,.05 = .338.

Since Dn = 0.1874988 < 0.338 = Dn,α, we conclude that the data is a reasonably good fit with the normal distribution. This is inconsistent with the QQ plot shown in Figure 5, which seems to show that the data is not normally distributed.

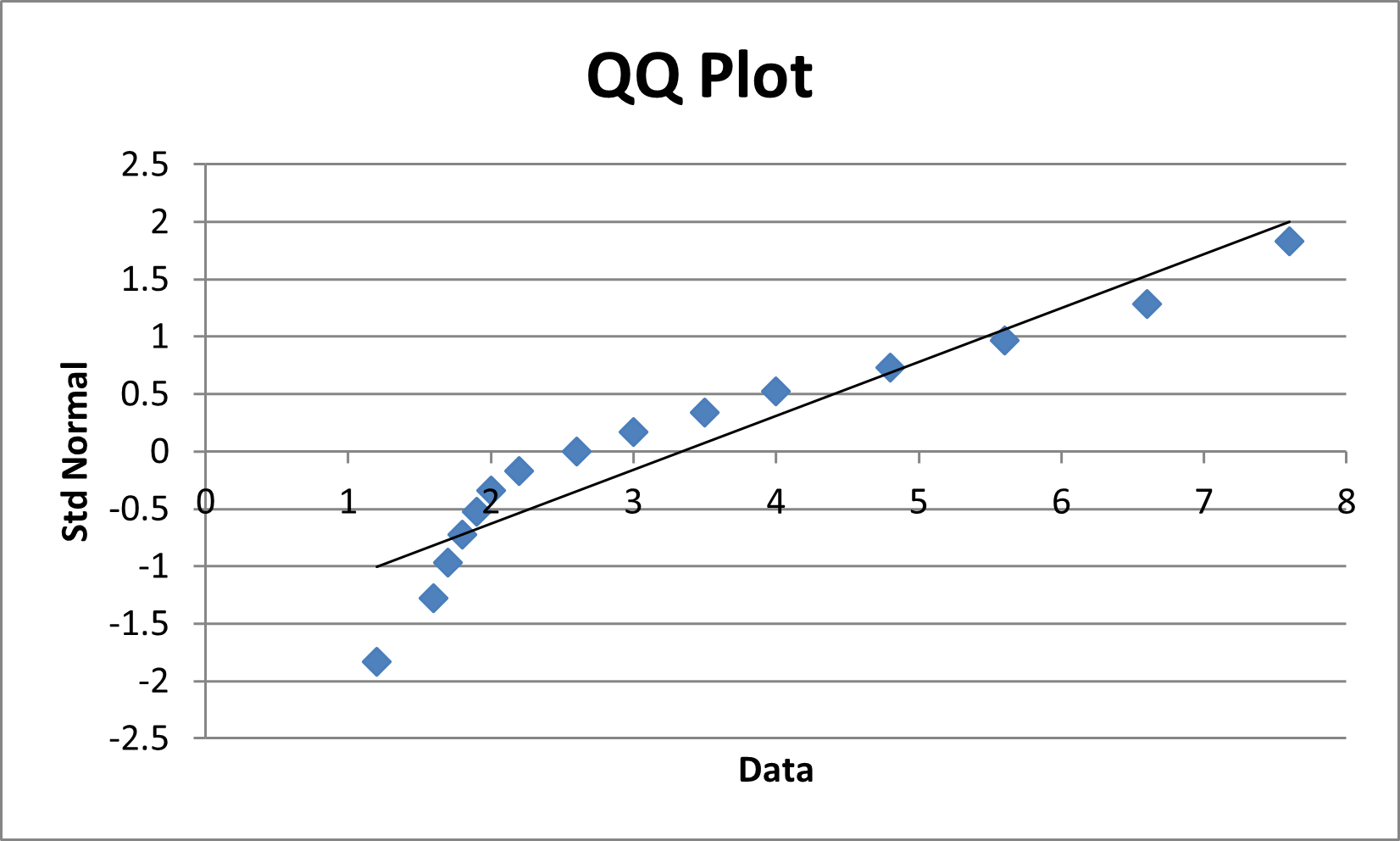
QQ plot

Figure 5 – QQ Plot for Example 2

The reason for this inconsistency is that the Kolmogorov-Smirnov test in the form presented above is only valid when the population mean and standard deviation are known, and not estimated from the sample. In the case where the population mean and standard deviation are not known, you need to use the Lilliefors version of the test, as described below.

Worksheet Functions

Real Statistics Functions: The following functions are provided in the Real Statistics Resource Pack:

KSCRIT(n, α, tails, interp) = the critical value of the Kolmogorov-Smirnov test for a sample of size n, for the given value of alpha (default = .05) and tails = 1 (one tail) or 2 (two tails, default), based on the KS Table. If interp = TRUE (default) then the recommended interpolation is used; otherwise, linear interpolation is used.

KSPROB(x, n, tails, iter, interp, txt) = an approximate p-value for the KS test for the Dn value equal to x for a sample of size n and tails = 1 (one tail) or 2 (two tails, default) based on a linear interpolation (if interp = FALSE) or recommended interpolation (if interp = TRUE, default) of the values in the Kolmogorov-Smirnov Table, using iter number of iterations (default = 40).

Note that the values for α in the Kolmogorov-Smirnov Table range from .001 to .2 (for tails = 2) and .0005 to .1 for tails = 1. When txt = FALSE (default), if the p-value is less than .001 (tails = 2) or .0005 (tails = 1) then the p-value is given as 0, and if the p-value is greater than .2 (tails = 2) or .1 (tails = 1) then the p-value is given as 1. When txt = TRUE, then the output takes the form “< .001”, “< .0005”, “> .2” or “> .1”.

Examples

For Example 2, KSCRIT(15, .05, 2) = .338 (the same as shown in cell H21 of Figure 4). Also note that the p-value = KSPROB(H20, B21) = KSPROB(0.184177, 15) = 1 (meaning that p-value > .2), and so once again we can’t reject the null hypothesis that the data is normally distributed.

If the value of Dn had been .35 in Example 2, then Dn = .35 > .338 = Dcrit, and so we would have rejected the null hypothesis that the data is normally distributed. In this case, we would have seen that p-value = KSPROB(.35,15) = .0427, which once again leads us to reject the null hypothesis.

Kolmogorov Distribution

As referenced above, the Kolmogorov distribution can be useful in conducting the Kolmogorov-Smirnov test. Click here for more information about this distribution, including some useful functions provided by the Real Statistics Resource Pack.

Lilliefors Test

When the population mean and standard deviation for the Kolmogorov-Smirnov Test is estimated from the sample mean and standard deviation, as was done in Example 1 and 2, then the Kolmogorov-Smirnov Table yields results that are too conservative. More accurate results can be derived from the Liiliefors Table as described in the Lilliefors Test for Normality.

Examples Workbook

Click here to download the Excel workbook with the examples described on this webpage.

References

National Institute of Standards and Technology NIST (2021) Kolmogorov-Smirnov goodness-of-fit test
https://www.itl.nist.gov/div898/handbook/eda/section3/eda35g.htm

Wikipedia (2012) Kolmogorov-Smirnov test
https://en.wikipedia.org/wiki/Kolmogorov%E2%80%93Smirnov_test

145 thoughts on “Kolmogorov-Smirnov Test for Normality”

  1. Good evening from Thailand.

    I have a question about if i want to do this test with my flood frequency data.

    I have to calculate F(x) from observe data or result data.

    Thanks !

    Reply

  2. Hello Charles,

    am i wrong or there is a difference with the way you find the critical value (Dn,α) in examples 1 and 2 ?
    In example 1, Dn,α was calculated and you use the number from Kolmogorov-Smirnov Table as a parameter.
    In example 2, the number from Kolmogorov-Smirnov Table is directly the Dn,α value.

    Thanks a lot for your help

    Reply

    • Hi Roy,
      Yes, that is true. For Example 2, you can find the critical value in the table since n <= 50. For Example 1, n is larger than 50 and so you need to make a simple calculation using the value in the last row of the table of critical values (for values of n > 50).
      Charles

      Reply

    • Hello Baani,
      What you are calling Dmax is called D_n on this webpage. Referring to Figure 3 on the webpage it is the largest value that appears in column G, namely the value in cell G10 (also shown in cell G15).
      CHarle

      Reply

  4. hi charles, i want a formula of mean ,standard deviation (sd),test (t) differences (df) and sig.2 tailed using only two variables

    Reply

  5. Good morning Charles,

    When I manually do the K-S method on my data I get a Dn = 0.1523
    With a sample size of 30 and a alpha of = .05 the Dn,a = .24.
    This should mean the data pass normality but when I verify on minitab, I get a Dn = .171 and a p-value = 0.033. Would you happen to know why minitab gives me a p-value significantly lower than than expected?

    Reply

    • Alex,
      I don’t know why you would get a different result when using Minitab. If you email me your data I can check whether your calculations are correct.
      Charles

      Reply

  7. Hi,
    I’m training with the example one but I got a doubt. Why in Standardized function do you use the x values (max value of the interval) and not the mid point of the interval?

    Reply

      • The example one shows how to fill the excel sheet:
        “the formula in cell E4 is =STANDARDIZE(A4,N$5,N$10)”
        Then to get the Z score you use cell A4. My question is: why do not use the midpoint (A4 is the up limit) of standardized if it a frequency distribution?

        Another question (thank you to help): when we use a hypothesis test for mean or standard deviation, if p-value < significance level we reject the null hypothesis.

        Then , for a normality test, we define as H0: the distribution is normal and Ha the distribution is not normal. So, if p-value is less than significance level we reject H0. For kolomogorov-smirnoff if the Dn is less than Dn,alpha it is accepted but it must be rejected instead?

        Reply

        • Hello Jacques,
          For the delayed response.
          1. You could use the midpoint.
          2. This depends on whether you are looking at a left-tailed or right-tailed test.
          Charles

          Reply

  8. Hi Charles
    I have read somewhere that the KS test is invalid if we use the data to find the location, shape and scale parameters. That is to say that the distribution need to be fully specified before hand for us to use this test. The examples all use the data to find the parameters of the distribution !

    Reply

  9. Hi Charles

    Interesting Article.. I’m quite new to performing KS tests in Excel. I’ve been testing for normality on a variable with 45 data points. I’ve been checking the resulting test statistic in SPSS and always get a matching figure, until I bring in the 45th data point then everything changes. My excel test statistic is 0.13873 however SPSS indicates it should be 0.160952 I am totally confused. Would you be able to let me know where I’ve gone wrong or explain why there is a difference? I’ve forwarded the spreadsheet in a seperate email – many thanks

    Reply

    • Hello Jon,
      I am not sure where the error is, but I notice that you never used the values calculated in column F.
      In any case, the Real Statistics KSSTAT calculates the KS statistics and the formula =KSSTAT(B4:B48) returns the value 0.160952, the same as SPSS. =KSSTAT(B4:B47) returns 0.132926.
      Charles

      Reply

  10. Hi Charles,

    Need your advice in finding p-value using KS test. If my test statistic D is 0.08772444 and n=42, I got p-value=1 by using =KSPROB( ) function. But if I want to get the exact value of p-value instead of 0 or 1, how can I do it?

    Thank you.

    Reply

    • Hi Jessica,
      Use the formula =KSDIST(0.08772444,42). This returns the value .888959. The KSDIST formula uses the Kolmogorov distribution, while KSPROB uses the table of critical values and so any value above .20 is returned as 1. See the following webpage for more information about KSDIST
      Kolmogorov Distribution
      Charles

      Reply

  11. I have two questions:
    1: Excel uses a fast way to calculate the CDF of a normal function (NORM.DIST, with the “cumulative” parameter set to true). This integral needs to be approximated numerically, but the help file from Microsoft does not provide any information how that is done, and which approximation is used. Do you know of a good numerical approximation that works for some specified mean and SD (but not 0 and 1, respectively)? I need to have the formula used, because I’d like to test it in Excel and then transport it to a programming language
    2: I would like to assess whether a set of 25 events with a continuous x-value between -2 and 2 is normally distributed. I plan to use the KS test for this, does that make sense?

    Reply

  12. Hi Charles,
    you are doing a great job by helping.
    I have my data on three variables, Income, Consumption, and Household size. the sample size is 250. I am stuck in normality. Can you help me test it so that i could defend it in my defense?

    Reply

  13. Dr.Charles Zaiontz, Thank you for the resourceful videos on statistics. How to perform the Kolmogorov-Smirnov test in spss when our independent variable is categorical (having 2 or 4 levels) and the dependent variable is an ordinal type scaled from 1 to 4? For eg: If my categorical variable is gender (2 levels: male & female) and my dependent variable is humor measured in an ordinal scale from 1 to 4. Kindly give your valuable suggestions and steps explaining it. Thanking you in advance

    Reply

    • Hello,
      I am not the person who released videos on performing the KS test in SPSS.
      In any case, you can perform the KS test with a categorical or ordinal independent variable. The dependent variable must be numeric. You can use ordinal data 1, 2, 3, 4, as long as you treat them as numeric data.
      See Kolmogorov-Smirnov Test.
      Charles

      Reply

      • Hello Dr.Charles Zaiontz,

        Thank you for your response. I will work it out as per your instructions.

        Thanking you.

        Reply

  14. Dear Charles

    With reference to “Example 2: Using the KS test”, I have done K-S test with my data below.
    But Dmax value is different from the value of minitab.
    – Dmax on KS-test = 0.2463, Minitab KS = 0.313
    Could you tell me why different ?

    Data(x) Rank sn(x) f(x) diff
    21.8935 1 14 0.9333 0.8190 0.1143
    21.898 1 15 1 0.8198 0.1802
    21.0919 1 6 0.4 0.6463 0.2463
    21.4778 1 8 0.5333 0.7368 0.2035
    21.5499 1 10 0.6666 0.7523 0.0857
    21.5106 1 9 0.6 0.7439 0.1439
    21.6473 1 13 0.8666 0.7724 0.0942
    21.571 1 11 0.7333 0.7568 0.0235
    21.1255 1 7 0.4666 0.6547 0.1881
    21.6359 1 12 0.8 0.7701 0.0299
    18.448 1 2 0.1333 0.0818 0.0515
    18.6285 1 5 0.3333 0.1016 0.2317
    18.3468 1 1 0.0666 0.0720 0.0054
    18.5553 1 3 0.2 0.0932 0.1068
    18.5758 1 4 0.266666667 0.0955 0.171166667

    mean 20.53038667 Dmax 0.2463
    stdev 1.495019933
    count 15

    I am looking forward to hearing from you.
    Thank you.

    Reply

    • I would need to see the calculations that you made. If you send me an Excel fil with the calculations you made, I will try to figure out what the issue is.
      Charles

      Reply

  15. Hi Charles,

    Thanks so much for this article and the software package!

    I was wondering is there any way in which the Kolmogorov-Smirov test can be used to show that two histograms are statistically similar? i.e. similar distribution, similar peaks etc… or is it best just to show that they’re both normally distributed (or otherwise)?

    Thanks,
    Michael

    Reply

  16. Dear Sir,
    Your example no 1 has proved highly useful to me. It is the example of grouped data, for which I was looking for, highly thankful. Sir can you explain how to apply Shapiro test on same example no 1 or anyother example of grouped data.
    Shall be grateful

    Reply

    • Dear Imran,
      You could do something similar for Shapiro Wilk where effectively you use the midpoint of the interval repeated several times (based on the frequency value). The only problem with this approach is that Shapiro-Wilk is probably not the best test with repeated data values. You could instead spread the values within an interval over the interval, but then you have the problem of how best to do the spreading.
      Charles

      Reply

      • Thanks alot sir, but do A.D test will also have same problem with the repeated data values. How A.D test can be conducted on grouped data? I have conducted K-S test and Lilliefors test on my grouped data but both have two differnt results K-S test shows data is normally distributed whereas lilliefors test shows it is not. Sir,pls suggest.
        Highly grateful

        Reply

  17. Hi,

    I see that Real Statistics offers KSCRIT and KSPROB functions for the 1 sample KS test; is there a function that computes the KS test statistic for the 1 sample test for normality? I also see that there is a KS2TEST function for the two sample test. Is there a KS1TEST function?

    Reply

  19. Hello Charles,

    After reading the different approach to test for normality, I still don’t understand what are the criterions (if any) for choosing a KS test over Shapiro-Wilk or a Chi squared ?

    Thank you,

    Yoan

    Reply

    • Yoan,
      In general, I recommend Shapiro-Wilk over KS or Chi-squared. SW does a better job of determining that data from a normal distribution is normal and data that is not from a normal distribution is not normal.
      Charles

      Reply

      • Thank you for your answer,

        I have a few questions on the example 2 thought, I performed the double tailed KS test in R on the same values and it returns me :
        D = 0,88493
        p-value = 1.254e-10

        How does one compute the p-value ? Is it the probability of
        F(Max Dn + Sn(x)) ?
        And do you know where does this D comes from ?

        Thanks again, your website is really great for self learner

        Yoan

        Reply

  21. Dear Charles,

    I have read with great interest the use of Kolmogorov Smirnov for testing normality. In the Figure 3 you have nicely explained the test, based on the example 1. However, I cannot figure out where the data for the F(x) column came from. You have pointed out that these data came from the NORMSDIST function from Excel, but I am interested in the actual equation for calculation of the Standard Normal Density Function. I have found that this distribution follows the following equation:

    F(x) = [e exp -(z exp 2)/2]/[Square root of (Pi*2)]

    This is the distribution function of a theoretical set of data with mean = 0 and Standard Deviation (and therefore variance) =1

    However, when I replace the z value in the equation, the resulting values do not correspond with the provided in Figure 3 for F(x). Could you provide us with the right equation, please? Thanks a lot for your help.

    Wilson

    Reply

    • Wilson,
      This is the formula for f(x), the pdf, and not the cdf, cumulative distribution function. The formula that you are looking for is the integral of f(x).
      Charles

      Reply

  22. My Kolmogorov-Smirnov is 0.000 significant, yet my supervisor wants me to have significant result, which is above 0.05, pleaseeeee someone help me. I don’t know how to to get significant result and what is affecting the komogorov test to increase or decrease

    Reply

    • M,
      If your supervisor wants a result above .05, then he wants a non-significant result (not a significant result).
      Unless you have made a mistake a p-value = 0 is a significant result. You can’t make it non-significant unless you change your data.
      Charles

      Reply

  23. Dear Charles,

    When i use KSCRIT(n=60 ; alpha=0.05) i get 0.1753, and when i use KSPROB(X=0.1753 ; n=60) the value is 0.0109. I checked the KS Critic but the obtained value for KSPROB is not logical even in the Kolmogorov Smirnov Table). Does function KSPROB has any restriction or problem?.

    Reply

    • Daniel,
      There is an error in the KSCRIT and KSPROB functions. Thank you very much for catching this error. I will fix it in the next release of the Real Statistics software, which I hope to issue shortly. I really appreciate your help in making the Real Statistics software more accurate and giving users confidence in the results obtained.
      Charles

      Reply

  27. Dear Sir,
    I am writing a java program to perform Kolmogorov Smirnov Test.
    So I want to know the mathematical formulae to calculate the Z-Score and F(x).
    And what does it mean by estimating population mean and standard deviation from the sample mean and standard deviation. Does it mean taking the mean and standard deviation of population same as sample mean and standard deviation.

    Thank You

    Reply

  28. Dear Sir,

    Is possible to determinate Dn parameter froma a data, using your Real Statistics addin. I was checking your examples and addin. However I cant find that formule.

    Reply

    • César,
      Sorry, but I have not yet implemented this is the Real Statistics addin. This value depends on the specific distribution that you are trying to fit and since there are so many distribution, I haven’t tried to create a single formula for this. I will look into doing this shortly.
      Charles

      Reply

  29. Dear Charles,

    Thanks for your application Real Statistics is ver useful
    However, I have some questions about the Kolmogorov-Smironov test.
    I have a huge sample of 3160 observations. My sample desribe a normal distribution, I can say that is a ideal sample.
    When I conduct K-S test on this data the null hypothesis is rejected.
    Why does it happen? I could expect that Ho was accepted!
    thanks for your response but I am new in this test,

    Best regards,

    Reply

    • Ruben,
      If you send mean Excel file with your data and the KS test that you have conducted I will try to figure out what is going on. You can send the file to the email listed on the Contact Us webpage.
      Note: You should use the Lilliefors version of the KS test for normality when you are estimating the the population mean and variance from the sample mean and variance.
      Charles

      Reply

  31. Charles, can you help me with what kind of normality test & hypothesis test that I should use with my survey?

    I created a survey about student’s perception on business ethics, based on gender (male / female), ethics education (formal / informal), & age of maturity (junior / senior). n = 160 with unequal distribution: 44 male – 116 female, 77 informal – 83 formal, 28 junior – 132 senior.

    Thank you in advance.
    DV

    Reply

    • Daniel,
      I suggest that you use the Shapiro-Wilk test for normality.
      Regarding the hypothesis test, first you need to determine what hypothesis/hypotheses you want to test.
      Charles

      Reply

  33. Hi Charles,
    Do you have a example of applying K-S test to check for conformance with Benford’s distribution. Do you think K-S method will be an appropriate method to check for deviation from Benford’s law.
    Thanks
    Santosh

    Reply

    • Santosh,
      Yes, I can see how you could use KS test to check or conformance with Benford’s law.I have not provided an example of this.
      Charles

      Reply

  35. Dear Charles
    Is it possible to get a conflicting result when the explore command and the one sample K-S are used to check the normality of the same data?

    Reply

    • I don’t know what “explore command” is.
      It is not surprising that two different tests for normality will give different p-values.
      Charles

      Reply

      • Thank you very much Charles.
        I dont know if I get it right, about numbers in column A (x values).
        Let me explain on this example.

        I have scale of loneliness and results can be
        10-20 – low loneliness
        20-30 – average loneliness
        30-40 – high loneliness
        so I calculate:

        data midp freq midp^2
        10-20 15 24 225
        20-30 25 32 625
        30- 40 35 33 1225

        So:
        n: 89
        M: 26,011
        Msq: 676,584
        Sq-sum/n: 739,606
        Varp: 63,022
        Var: 63,738
        Stdev: 7,983

        x freq Cum Snx Z F(x) D
        15 24 24 0,270 -1,379 0,084 0,186
        25 32 56 0,629 -0,127 0,450 0,180
        35 33 89 1 1,126 0,870 0,130

        Dmax 0,185
        Dkrit 0,144

        0,185>0,144 so data is not normally distributed.

        Is this rigt calculated or not?, I am not sure about choosing data for column A.

        Reply

        • Rob,

          If you assume that the data in each interval is concentrated at the midpoint then the calculation is correct. I have typically assumed this for the calculation of the mean, but have used the right end-point of the intervals for the KS calculation. I can see advantages with both approaches.

          I suggest that instead of using the KS table to calculate the critical value you use the Lilliefors Table instead. It is more accurate for determining whether data is normal when you use the sample mean and standard deviation. See the following webpage:

          Lilliefors Test

          Charles

          Reply

  37. Dear Sir,

    Thank you very much, I’m learning a lot from your website.

    Unfortunately, my data set dose not fit with normal distribution.

    I have very large data and I read in this paper (Open Access): Langlois, T. J., Fitzpatrick, B. R., Fairclough, D. V., Wakefield, C. B., Hesp, S. A., McLean, D. L., … Meeuwig, J. J. (2012). Similarities between Line Fishing and Baited Stereo-Video Estimations of Length-Frequency: Novel Application of Kernel Density Estimates. PLoS ONE, 7(11), 1–9. doi:10.1371/journal.pone.0045973

    “We used Monte Carlo simulations to overcome uncertainty regarding the asymptotic distributions of KS test statistics under the null hypothesis”.

    How can I do the simulation in excel so my data can fit with normal distribution, so I can run the KS test for my data.

    Thank you very much

    Reply

  38. Dear Charles I appreciate your contributions.

    Please consider the following, in your second example you state the following:

    “Since Dn = 0.1874988 < 0.338 = Dn,α, we conclude that the data is a reasonably good fit with the normal distribution (more precisely that there is no significant difference between the data and data which is normally distributed). Note that is not the same conclusion we reached from looking at the histogram and QQ plot"

    So the same remains for Dn = 0.1874988 .338 = Dcrit, and so we would have rejected the null hypothesis that the data is normally distributed. In this case we would have seen that p-value = KSPROB(.35,15) = .0427, which once again leads us to reject the null hypothesis”

    But if the α=0.01 then the critical value is 0.404 and Dn = 0.35 < 0.404 = Dn,α,

    Then, should we conclude that data is normally distributed ???

    I´ll appreciate your comments,

    Kind regards

    Edgar

    Reply

    • Edgar,
      Changing the value of alpha from .05 to .01, changes the value for Dcrit, but doesn’t change the value of Dn. I don’t see where the Dn = 0.35 comes from?
      The null hypothesis that the data comes from a normal population cannot be rejected if Dn < Dcrit. Charles

      Reply

  39. Charles, thanks, but I too have a question.

    May I perform the KS test on two samples with different counts or n values?

    For example, there are 7 possible categories, and there are 3 individual samples that will distribute within those 7 categories (dealing with sediment, sieves, and weights). I need to compare this set of samples to another set of samples, however, the number of samples here is 7. So, 2 sets of samples. The first, has 3 samples, and the second has 7. There are 7 sieve sizes or categories into which the samples are distributed. Can KS test be run on them?

    If not, then would it be permissible to take the means of each sample, thus giving congruency to the data (same n values, but with means), and use the n from the sample size (n=10 (3 from first, and 7 from second)), rather than the mean (n=2) to establish the critical value, or would I need to use the n from the mean sample size to establish the CV?

    Thanks,
    Brody

    Reply

  41. Dear Sir,
    Thank you for sharing this.
    I have a question: why in the first example we calculate the Z-score with x=100, 200, etc., but with mean and standard deviation calculated from the mid points (150, 250, etc.)?
    Shouldnt’e be correct to have the mid points of the intervals in column A for Z-score calculation?
    Best regards,
    Gianma

    Reply

    • Gianma,
      Probably either approach is acceptable, but here I have used the endpoints of the various intervals with the mean and stdev based on the midpoint of the intervals.
      Charles

      Reply

      • Dear Charles,
        Sorry for insisting, but it’s not a negligible difference: using the midpoints of the intervals for calculating the Z-score, the resulting Dn is equal to 0.117>Dn,a, so the overall result is the opposite (the data is NOT a good fit with the normal distribution)…
        Considering that the definition of Z is (Xi-u)/S, where u is the mean of the X values and S is their stdev, I think that only the midpoints of the intervals should be used, if u is calculated as their mean.
        Otherwise, we can use the endpoints of the intervals as Xi, but in this case also mean and stdev should be calculated on these values, and not on the midpoints.
        Do you agree?

        Reply

        • Gianma,

          I realize that depending on the choice you make you might come to a different conclusion. This is why it is important to view significance values such as alpha = .05 not as absolute things. In fact if you set alpha = .05 as your significance value, any p-value near .05 can be viewed with some caution.

          Unfortunately, this is the nature of statistics. If you get a p-value of .0003 you are fairly confident of your result (at least as far as type I error is concerned), but often depending on which test you choose to use (or which version of a test you use), you might get different outcomes.

          Charles

          Reply

          • Dear Sir,
            Thank you for your answer. Sincerely, I’m not 100% convinced, but at least this discussion forced me to look deeper into this topic, and review some forgotten page of statistics!
            Best regards,
            Gianmarco

  42. Great article. I know understand how you calculate the P value for the KS test. Thanks so much. However when I try to replicate in excel, the NORMDIST function does not return the same values. Is there something different you are doing, as excel is asking me for the mean and stDev (which i input) but does not return the same values you have in your sheet

    many thanks

    Reply

    • Avi,
      I don-t see any reference to the NORMDIST function on the referenced webpage. There is a reference to =NORMSDIST(E4(, which is the standard normal distribution function (mean = 0 and standard deviation = 1).
      Charles

      Reply

  44. Charles,

    with your tool it is possible to use the Shapiro-Wilk-Test on a time series and get a besides the p-value a “yes” or “no” for the normal assumption. Therefore I can do this test for multiple series parallel with only one formula which is very nice.

    Is there also a possibility to test for other distributions (Poisson, Stuttering Poisson, Gamma, Negative Binomial, etc.) for multiple series (KS-Test or Chi-Square-Test), so I can see which distribution would fit best?

    Sven

    Reply

  47. Hi all,
    I am trying to fit an appropriate probability distribution with my data. I have known that I can use K-S test, but my problem is that, as I am going to use MATLAB or EXCEL softwares for this purpose, I do not know how I can use these softwares for this test. My problem is that I have not ever seen any example of this test for exponential or other distributions rather than normal and lognormal distributions. How can I decide whether for example lognormal distribution is appropriate or exponential distribution?
    Thank you very much for your help inn advance.

    Reply

    • Hi Zohreh,
      The approach for using the KS Test to test whether the data is exponentially distributed is very similar to that shown on the referenced webpage. I will add an example using the exponential distribution to the website in the next couple of days. This should help you.
      Charles

      Reply

  48. Sir,

    I am trying to determine if Rokeach value survey (RVS) responses for two different groups are statistically significant. The RVS has subjects rank 18 values in order of importance to them. I have calculated the mean response for each value within each group and ordered them from most important (lowest mean) to least important (highest mean). I was told I could use the Kolmogorov-Smirnov Test to determine if differences in mean value rankings between groups are statistically significant.
    I would appreciate an explanation of this process in Excel.

    Thank you in advance,
    Kevin, Excel expert, stats neophyte

    P.S. I have learned more practical statistics from your site than my undergrad and masters professors have been able to drill into me… Well done, Sir!

    Reply

    • besides that is it possible to use the statistical value of other distribution as a critical value to find the p-value of KS test?
      for example, use the z value of normal distribution to find the p-value by KS test.

      Reply

      • Sally,
        Sorry, but I don’t understand your question. In any case I will be adding the KS p-value shortly.
        Charles

        Reply

    • Sally,
      I have now provided a way of calculating the p-value for the KS test, using the functions KSPROB and KSDIST. These are available in the latest release of the Real Statistics Resource Pack (Rel 2.15).
      Charles

      Reply

  50. hello sir, i found this article very helpful. i need to fit log normal distribution either from chi square or K-S test. you have explained only normal distribution. please explain log normal distribution also.
    here is my test data
    mean= 5.1439
    δ= 0.2506
    median= 4.99
    σlnz = 0.247

    interval observed frequency
    1.81 2.759 9
    2.759 3.708 61
    3.708 4.657 116
    4.657 5.606 155
    5.606 6.555 120
    6.555 7.504 42
    7.504 8.453 7
    8.453 9.402 2
    9.402 10.351 2
    10.351 11.3 3
    sum= 517

    Reply

    • The procedure for using the K-S test with the log normal distribution is pretty much the same as for the normal distribution. E.g. in Figure 3, you won’t need the E column. Simply enter the formula for the log-normal distribution in column F. E.g. cell F4 would contain a formula like =LOGNORMDIST(A4,N5,N10). The rest is the same as in the examples provided on the webpage.
      Charles

      Reply

      • thank you very much sir for your reply.
        sir i have one more doubt, should we use “mean and standard deviation” or “Median and σlnz in lognormal distribution?

        Reply

        • Sandeep,
          If I understand your original question correctly, then you should use the mean and std dev, esp. since Excel has the LOGNORM.DIST function available which use these two parameters. Why do you think the median and σlnz might be good choices? Perhaps this is correct and I am not answering the right question.
          Charles

          Reply

        • Hi Bruno,

          If you know the distribution parameters (e.g. mean and variance for the normal distribution) then the table of critical values is the same. Usually these parameter values are estimated from the sample, in which case different critical values should be used. I have provided the table for the normal distribution. This is call the Lilliefors Test. See the following webpages

          Lilliefors Test
          Lilliefors Table

          Charles

          Reply

Leave a Comment