Property 1:
S(t) = e–H(t)
or equivalently
H(t) = −ln S(t)
Proof: Since S(t) = 1 − F(t), the derivative S′(t) = − F′(t) = − f(t). Thus
Taking the integral of both sides yields
From which we get H(t) = -ln S(t). Taking the exponential of both sides yields the first result.
Observation: Some properties of the hazard function are
Observation: If the hazard function is constant then t has an exponential distribution; i.e. a constant hazard function corresponds to an exponentially distributed lifetime. To see this, let
Then c(1−F(t)) = F′(t), which has a solution when F(t) = 1 − ce-ct. Alternatively
Reference
Wikipedia (2015) Survival analysis
https://en.wikipedia.org/wiki/Survival_analysis#:~:text=Survival%20analysis%20is%20a%20branch,and%20failure%20in%20mechanical%20systems.
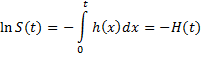
i want to survival analysis part
What specifically are you looking for?
Charles
Hello Dr, am very happy with all materials I read in your site sir, I wish to make you as my mentor sir…
Joseph,
I am very pleased that you like the materials on the website.
Charles
Good day. I am a PhD student in Nigeria researching on a topic ‘Information technology skills, demographic and institutional factors as correlates of doctoral degree completion in Nigerian Library Schools. I used survival analysis theory as the theoretical framework. I want to find out if this theory can actually be used for this study.
Thank you as I look forward to your quick response.
Yusuf,
Whether it is appropriate for your specific study, I can’t say, but, in general, survival analysis can be used in studies about completion of a school degree.
Charles