Hazard Ratio

Definition 1: The ratio of the observed number of failures (“deaths”) divided by the expected number of failures d/e (using the terminology from Log-Rank Test) is called the failure rate. For two survival distributions, the ratio of the failure rates is called the hazard ratio (aka the relative risk or risk ratio), i.e.

image056x

For Example 1 of Log-Rank Test, the failure rates of trials A and B are 12/9.828 = 1.221 and 8/10.172 = .786. Thus the hazard ratio h (of A to B) is 1.55. Since h > 1, the drug in trial B has a more favorable survival rate than the drug in trial A (in fact 55% more favorable).

A confidence interval for h can be calculated based on the fact that ln h is approximately normally distributed with standard error

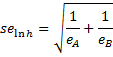
image057x

This approximation is fairly good for values of h between 1/3 and 3.

For Example 1 of Log-Rank Test

image058x

Thus, we see that the 95% confidence interval for the hazard ratio in Example 1 of Log-Rank Test is (.646, 3.730), as shown in Figure 1 (with references to the cells in Figure 3 of  Log-Rank Test).

Hazard ratio

Figure 1 – Confidence interval for hazard ratio

26 thoughts on “Hazard Ratio”

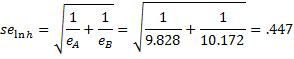
  1. Hi Charles, Thank you for the amazing work you have done on the website. I was wondering if you could help me with a doubt about hazard ratios (HR). I have access to a publication reporting HR of death given exposure A obtained from Cox regression. These are reported by sex (males and females) and by age categories. What I would like to have is age and gender-specific HRs. Can the HR simply be multiplied to obtain the desired hazards?

    Reply

    • Hi Rui,
      I am not sure which HR’s you want to multiply, but the formula for HR is the first formula shown on this webpage. As long as what you want to do is consistent with this formula, you should be ok.
      Charles

      Reply

  2. Hi Charles,

    Thank you for your hard work with all these interesting topics. I have a question regarding the HR estimation. It turns out that the estimated HR from Logrank test is approximate, but not equal to the HR estimated directly from the Cox proportional hazards model, when only one covariate (the variable group) is included. I guess this is because the methodology for the HR estimation is different when comparing Logrank test and Cox model.

    My question is how the standard errors of HR are calculated in the Cox model, and whether there is any advantage of calculating the HR from the Logrank test rather than obtaining this estimation directly from the Cox model.

    Kind regards,

    Wilson

    Reply

  4. Like Joost and Edwin said, hazard ratio and relative risk are not exactly the same even though they are commonly used interchangeably. Hazard ratio is an instantaneous risk meaning the risk of failure at time t given that the subject has survived up to the beginning of the the time interval (or up to t-1) while relative risk is usually a cumulative risk during the entire follow-up time. Hazard ratio is similar to incidence density ratio (incidence rate ratio) in which the denominator for incidence density is person-time.
    See additional notes here: https://en.wikipedia.org/wiki/Hazard_ratio

    Reply

  5. Hi there – this website is so helpful! Quick question, how did you come to 68% more favorable? I assume the numbers are rounded, but I can’t for the life of me get the same percentage.

    Thank you for your time!

    Reply

    • Megan,
      Sorry for the confusion. I believe that the 68% was left over from an earlier example. The value should be 55%.
      Thanks for identifying the error on the webpage.
      Charles

      Reply

  6. Two questions:

    1. is the hazard ratio same as risk ratio?

    2. how to compute the expected number of death in each group?

    Please be specific, Thanks!

    Reply

Leave a Comment