The hazard function at any time tj is the number of deaths at that time divided by the number of subjects at risk, i.e.
If dj > 1, we can assume that at exactly at time tj only one subject dies, in which case, an alternative value is
We assume that the hazard function is constant in the interval [tj, tj+1), which produces a step function. The standard error of h(t) is
By Property 1 of Basic Concepts of Survival Analysis, the cumulative hazard function is represented by the formula
As shown in the proof of Property 1 of Kaplan-Meier Theory, it follows that the standard error of H(t) is
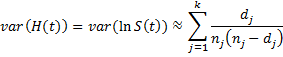 Reference
Reference
NCSS (2015) Kaplan-Meier curves (Logrank tests)
https://www.ncss.com/wp-content/themes/ncss/pdf/Procedures/NCSS/Kaplan-Meier_Curves-Logrank_Tests.pdf
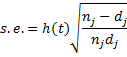
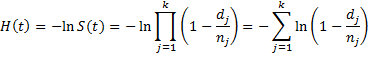
Hello Dr. Charles Zaiontz, how are you?
I would be so grateful, if you tell me how can I add a Survival distribution function S(t) overtime in a Cox Proportional Hazard method? I’d like to add the same chart available in the Kaplan-Meier approach.
Best Regards,
Raphael
Raphael,
Have you looked at the various topics at the following two webpages:
https://real-statistics.com/survival-analysis/kaplan-meier-procedure/ (for Kaplan-Meier)?
https://real-statistics.com/survival-analysis/cox-regression/ (for Cox Proportional Hazard method)
Charles
Dear Charles,
Need your help for creating
a) Kaplan Meier Hazard curve
b) Nelson Aalen Hazard curve
Am not from the Mathematical field and honestly do not understand if they are two different things
Need it for a clinical trial, related to risk for an event with time on X axis
Please suggest which would be better if the two are different
Dr Anitha,
Please see the following webpage regarding Kaplan-Meier
Kaplan-Meier
I am not familiar with the Nelson Aalen harzard curve.
Charles
Yes I have used it from your web page and it was very useful
The problem in using is as follows
I am writing about patients landing up in more and more severe levels of kidney failure over time
When I use survival curve – It conveys how many of them did not get into that stage
When I use hazard curve – it conveys how many of them got into those severe stages
That is the reason I was looking for hazard curve
Regards
Dr Anitha