We now show how to estimate the standard error and confidence intervals for the estimated survival function at any time t based on the Kaplan-Meier procedure.
Standard Error
Property 1 (Greenwood): The standard error of S(t) for any time t, tk ≤ t < tk+1 is approximately
Proof: See Kaplan-Meier Theory
Observation: If there is no censored data, then nj+1 = nj − dj, and so
Thus
Since S(t) = nk+1/n, the variance for S(t) is approximately
Confidence Interval
Property 2: The approximate 1−α confidence interval for S(t) for t, tk ≤ t < tk+1, is given by the formula
where zα/2 = NORM.S.INV(1−α/2).
Proof: See Kaplan-Meier Theory
Example
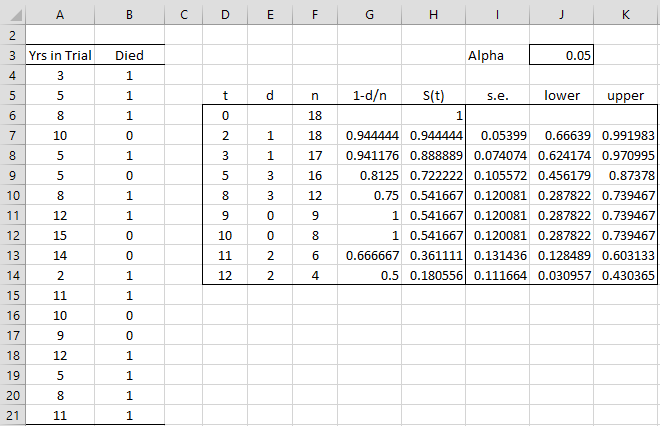
Example 1: Find the 95% confidence intervals for the survival function in Example 1 of Kaplan-Meier Overview.
The results are shown in Figure 1.
Figure 1 – Kaplan-Meier including confidence intervals
Figure 2 shows key formulas from Figure 1.
| Cells | Entity | Formula |
| I7 | s.e. | =H7*SQRT(E7/(F7*(F7-E7))+(I6/H6)^2) |
| J7 | CI-lower | =H7^EXP(NORM.S.INV($J$3/2)/LN(H7)*I7/H7) |
| K7 | CI-upper | =H7^EXP(-NORM.S.INV($J$3/2)/LN(H7)*I7/H7) |
Figure 2 – Key formulas from Figure 1
Examples Workbook
Click here to download the Excel workbook with the examples described on this webpage.
References
NCSS (2015) Kaplan-Meier curves (Logrank tests)
https://www.ncss.com/wp-content/themes/ncss/pdf/Procedures/NCSS/Kaplan-Meier_Curves-Logrank_Tests.pdf
Sullivan, L. (2016) Estimating the survival function
https://sphweb.bumc.bu.edu/otlt/MPH-Modules/BS/BS704_Survival/BS704_Survival4.html
Sachs, M. C., Brand, A., Gabriel, E. E. (2022) Confidence bands in survival analysis
https://www.nature.com/articles/s41416-022-01920-5
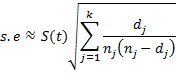
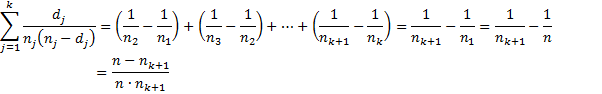
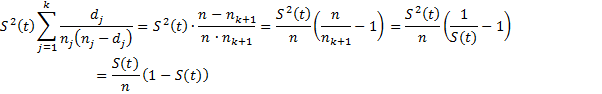
Thank you, this was very relevant to a recent task I had to solve!
Greetings from India!
Sir, I am Facing circular reference issue with respect to the above method through Excel.
Hello Charu,
Greetings from Italy.
Can you send me an Excel file so that I can see the circular reference? I will try to see what is going wrong.
Charles
Hello Charles, congratulations for the fine work and thanks for giving us the chance to learn with you. I was trying to compare a Kaplan-Meier survival graph with a given distribution. I found no reference in this regards. Is this a bad idea?
Hello Edward,
Glad to read that the Real Statistics website has been helpful.
Sorry, but I don’t have a reference for such a comparison. I don’t know why you want to do this and so can’t comment as to whether this is a good idea. If I needed to make such a comparison, I would do one or both of the following: (1) Graph both and visually compare them or (2) use the log-rank test (creating a sample from the data from the distribution).
Charles
Happy New Year Charles and thank you for the wonderful website!!!!!
Ruth
Thank you, Ruth, and Happy New Year to you.
Charles
Hi Charles,
Great job! Any chance that you can post SE calculation if there are censored observations?
Thank you in advance!
Hello Andy,
Property 1 shows the SE when there are censored observations.
Charles
Hello Dr. Zaiontz, is it possible to calculate uncertainty for the number of weeks to reach S(t)? For example, I have a survival series and S(t) is <= 0.5 at 12 weeks. Could I calculate uncertainty around 12 weeks? I am sorry if this is confusing. Thanks for your consideration
Peter,
I don’t know of an approach for doing this. All I can think of at the moment are the following three approaches, although I don’t have any evidence that any of these is appropriate. (1) Use a weighted average of the lower and upper ends of the confidence intervals in the output described on this webpage. Perhaps the weighting could be based on the interval sizes. (2) Another approach is to do something similar with the standard errors and then calculate the confidence interval based on this standard error. The usual approach for calculating the pooled standard error for a two-sample t-test might be appropriate. (3) Some sort of resampling technique might work.
Charles
Hi Charles,
Can you clarify why for the CI you divide the SE by the survival (i.e. I7/H7) when the formula in property 2 does not includes this.
Thanks
Santi
Hello Santi,
I believe this is the way I handled the sum, but I need to check this to make sure.
Charles
First, Charles, thanks for the site and the software. It’s great.
Regarding the formula for the CI. It relies on the transformation L = Ln(-Ln(S)). If you don’t make this transformation, you can get bounds for S that are 1. The variance of L(S) is 1/(LN(S))^2*SUM instead of S*SUM as given under Property 1 above. You get the confidence bounds on L(S) and then go backwards: S = exp(-exp(L)). That’s why the formula for the confidence bounds doesn’t look like what we expect.
Hello Michael,
Thank you for your comment about the CI. I believe that I used the approach described in Stata: see page 2 of the following webpage
http://fmwww.bc.edu/RePEc/bocode/s/stcband.pdf
Are you saying this is incorrect or did I just implement it incorrectly? I looked on your website for a clarification of this issue, but couldn’t find it. Can you point me in the correct direction?
Charles
Thanks for your comment but pls can you give citation for your claim as it might be of help to my study.
Thanks very much too Dr Charlse
HI Charlie what is LN in the following “=H7^EXP(NORMSINV($J$3/2)/LN(H7)*I7/H7)”
This is the natural log. See
https://real-statistics.com/mathematical-notation/exponentials-logs/
Charles
Hi,
Is this procedure applicable to Net Survival CI95% estimation?
I am trying to extract from de CI95% of the Net Survival (obtained in STATA, Pohar Perme) the SE but it doesn´t work. The estimations obtained in STATA and manually whith this Excel procedure are different.
Thank you!
Amaia
Hello Amaia,
Sorry, but I don’t know what the difference is between Net Survival and Survival. I don’t use STATA.
Charles
splendid , clear, understandable and precise
Is the formula for the s.e. correct? I6 is an empty cell in that dashboard.
Vitor,
It is true that cell I6 is empty, and so in the formula for se, =H7*SQRT(E7/(F7*(F7-E7))+(I6/H6)^2), cell I6 will have the value zero. But this same formula will be copied into all the other cells in column I. When copied into the next row, the formula will become =H8*SQRT(E8/(F8*(F8-E8))+(I7/H7)^2). This time cell I7 won’t be empty.
Charles
I have found your formula for S.E. and confidence intervals most helpful. Is it possible to display these on a graph using excel?
James,
Yes, you can display an Excel chart with the confidence intervals. You can use the same approach as shown for linear regression on the following webpage:
Confidence and Prediction Interval Plot
Charles
Hi Charles,
I am evaluating data from an insecticide trial. For some of the insecticides, there is high mortality before the first time point, so that the value for F7-E7 is negative. For example, at the first time point 8 of the 12 insects are dead, so the s.e. can’t be calculated because of the negative value. Is this correct — that the standard error can’t be calculated in this instance?
Thank you
Paul,
If you send me an Excel file with your data and test results, I will try to figure out what is going on.
Charles
Hi Charles,
I could be wrong, but I believe there is an error in the formulas above for the “CI-lower” and “CI-upper” cells. The formula shown in Property 2 looks like what I believe to be true, but for example, the “CI-lower” in J7 does not divide out the S(t) that is present in I7. I think it should read:
“=H7^EXP(NORMSINV($J$3/2)/LN(H7)*I7/H7)”
Let me know if I’m missing something.
Thanks
Brian,
You are completely correct. I have just changed the website to reflect the changes necessary. Shortly, I will put out a new release of the Real Statistics software with this correction.
Thank you very much for finding this error and bringing it to my attention.
Charles
No problem. I’m glad I could help.
Brian