Real Statistics Capabilities for Cox Regression

Worksheet Functions

Real Statistics Functions: The Real Statistics Resource Pack provides the following array functions:

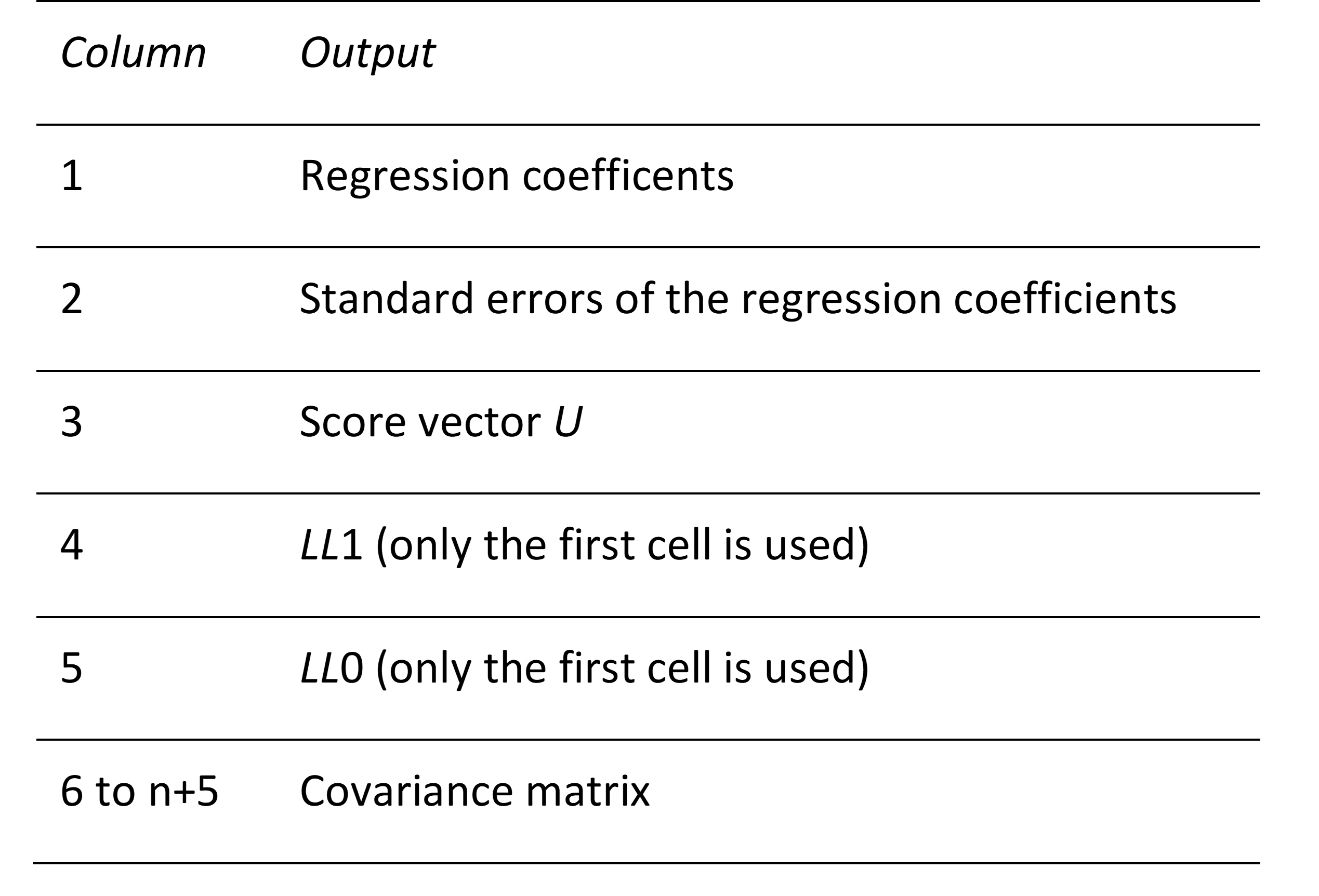
COXEST(R1, approx, iter) – n × n+5 array as described in Figure 1 based on the data in the m × n+2 range R1 formatted as in range B4:E21 of Figure 3 of Cox Regression using Solver. The approx parameter takes the value: 0 if the continuum approximation is used, 1 if the Breslow approximation is used, or 2 if the Efron approximation is used, default is 1; the Efron approximation is not currently supported. The output is calculated using Newton’s Method with iter iterations (default = 20).

Figure 1 – COXEST output

Note that the continuum approximation is the one used when d_j = 1 for all time periods. When there are multiple deaths in some time periods, then the assumption is that the time periods are slightly different (in some semi-random order). The Breslow and Efron approximations are described in Cox Regression with Ties.

COXPRED(R1, R2, R0, lab, approx, iter, alpha) – predicts the hazard ratio between the two subject profiles in the n × 1 column or 1 × n row ranges R1 and R2 based on a Cox regression model derived from the input data in the m × n+2 range R0. The arguments approx and iter are as for COXEST. The alpha argument is the significance value (default .05). If lab = FALSE (default), the output is a 4 × 1 range containing the hazard ratio, the standard error and the lower and upper limits of the 1 – alpha confidence interval. If lab = TRUE then the output is a 4 × 2 range whose first column contains row labels.

We can use the array formula

COXPRED(AK21:AK22,AL21:AL22,B4:E21,TRUE)

in range AN21:AQ22 (where B4:E21 is the model’s input data as shown in Figure 1 of Cox Regression using Solver) to address Example 3 of Cox Regression using Newton’s Method, as shown in Figure 2.

Figure 2 – COXPRED output

Data Analysis Tool

Real Statistics Data Analysis Tool: The Real Statistics Resource Pack provides the Cox Regression option to the Survival Analysis data analysis tool which implements Cox regression.

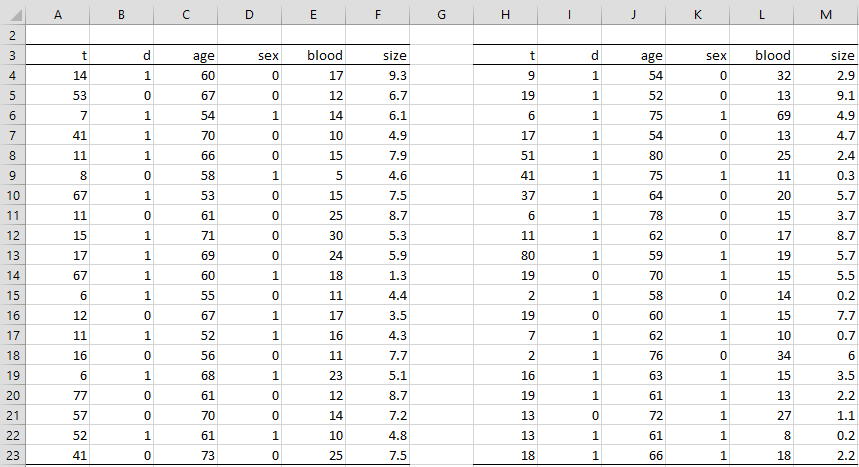
Example 1: Perform Cox regression for the study of the 40 patients shown in range A3:F43 of Figure 11 (the second 20 patients are repeated in range H4:M23 of Figure 3 so that they would fit on the page more easily). Each patient is being treated for liver cancer and the number of months of survival is recorded until the patient dies (d = 1) or leaves the study or has not died when the study ends (d = 0), along with the patient’s age, sex (0 = male, 1 = female), the value of a new blood test and the size of the tumor at the start of treatment.

Figure 3 – Liver Cancer Study Data

To use the Real Statistics Cox Regression data analysis capability for Example 1, press Ctrl-m and select the Survival Analysis option (from the Misc tab if using the Multipage user interface). Next, fill in the dialog box that appears as shown in Figure 3, and click on the OK button.

Figure 4 – Survival Analysis dialog box

Output

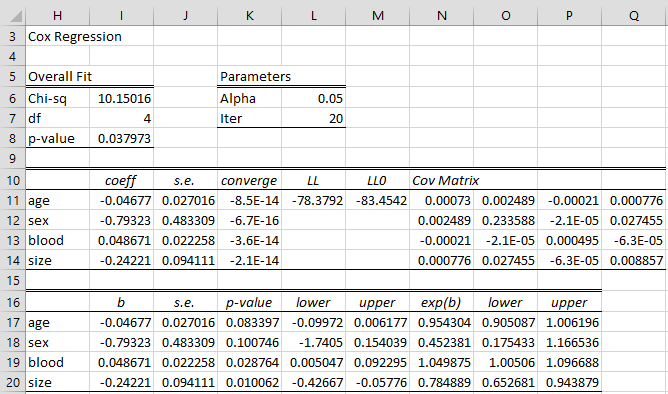
The output is shown in Figure 5.

Figure 5 – Cox Regression data analysis tool output

Note too that the array formula =COXEST(A4:F43,1,20) produces the output shown in range I11:Q14 of Figure 5.

Log-Rank Test Example

Example 2: Repeat Example 3 of Log-Rank Test using Cox Regression.

The data for this example is shown in Figure 6 of Real Statistics Support for Kaplan-Meier (the first 12 elements of which are repeated in Figure 6 below). Using Real Statistics’ Cox Regression data analysis capability (filling the Input Range 1 field of Figure 3 with A3:C39) we obtain the output shown in Figure 6.

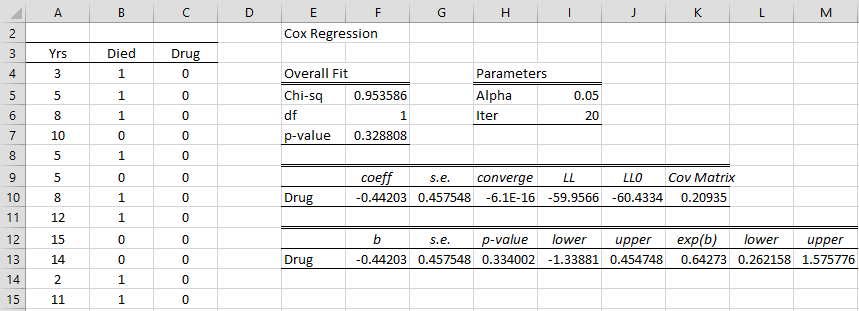
Figure 6 – Cox Regression comparing two drugs

Since the hazard ratio = exp(b₁) = .64273 (cell K13), we see that an increase of 1 in the Drug covariate results in a reduction of 35.7% in the risk of death. But such an increase is simply a comparison of Drug A (covariate = 0) with Drug B (covariate = 1), and so Drug B reduces the risk of death by 35.7% over Drug A (although, as we see from Figure 6, the 95% confidence interval is quite wide).