Introduction
We now show how to calculate the Cox regression coefficients using Solver for the model:
where X is a list of random variables x1, …, xr. This model is equivalent to
Now for any subject s in the sample with values xs1, …, xsr for the r covariates, we define
We assume that time is divided into the following intervals t0 < t1 < ⋅⋅⋅< tm where t0 is the start time and tm is the time of the last observed death. The risk set Rj is the set of all subjects who survive to the time just before tj. Thus the risk set consists of all those who die at time tj or who are censored or die after time tj.
Let Dj be the set of all subjects who die at time tj. nj = the number of survivors just before time tj (i.e. the number of elements in Rj) and dj = the number who die at time tj (i.e. the number of elements in Dj) and no one dies between times tj and tj+1.
We further assume that dj > 0 for each j (i.e. we won’t assign times tj for censored data unless a subject also dies at that time).
In fact, initially, we will assume that dj = 1 for each j. If we consider time as a continuum, then this is a reasonable assumption since two deaths are unlikely to occur at precisely the same time. If we think of time in discrete steps (as we have until now), then this assumption is too restrictive. For now, we will stick with this assumption, but we will return to this issue later.
Likelihood function
If dj = 1 for each j, then the partial likelihood function is
where xji is defined to be xsi where s is the unique element in Dj. Similarly, gj(X) is defined to be gs(X) in this case.
The natural log of L is then
As we have done for logistic regression, our goal is to find the coefficients b1, …, br which maximize LL. First, we show how this is done using Excel’s Solver and then we will use Newton’s Method, which will also provide additional information.
Example
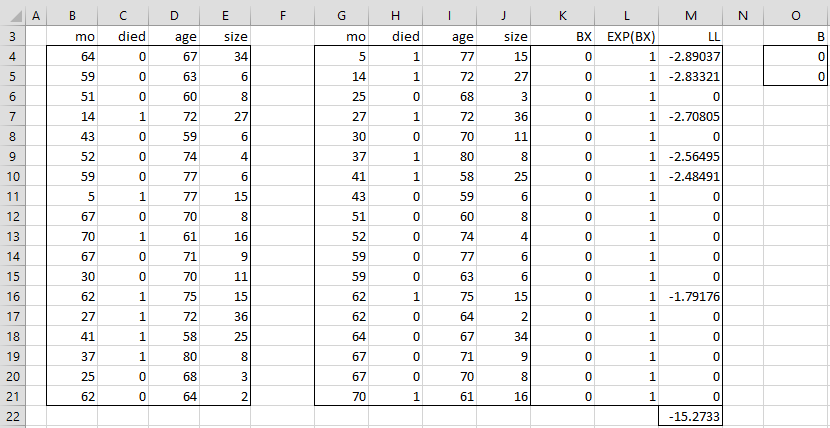
Example 1: Find the coefficients for Cox regression for the clinical trial for 18 patients shown in range B3:E21 of Figure 1. Here each patient is given an experimental drug for the treatment of lung cancer and the number of months of survival is recorded until the patient dies (died = 1) or leaves the trial or has not died when the clinical trial ends (died = 0), along with the patient’s age and the size of the tumor at the start of treatment.
We begin by sorting the data by the number of months of survival, as shown in range G3:J21 of Figure 1. We can do this by using Excel’s sort capability (Data > Sort&Filter|Sort) or by using the Real Statistics formula =QSORTRows(B4:E21). Since we assume that deaths precede censored data, we need to make sure that the patient in range G16:J16 comes before the patient in range G17:J17 (since both survive 62 months).
Figure 1 – Cox Regression (initial state)
We now find the value of LL by placing the array formula =MMULT(I4:J4,$O$4:$O$5) in cell K4, the formula =EXP(K4) in cell L4 and the formula =IF(H4=1,K4-LN(SUM(L4:L$21)),0) in cell M4. We then highlight the range K4:M21 and press Ctrl-D. Finally, we place the formula =SUM(M4:M21) in cell M22.
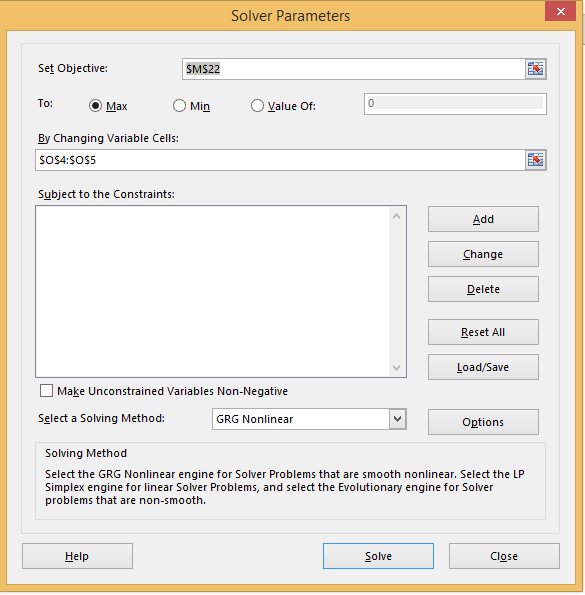
We see from Figure 1 that when b1 = b2 = 0, LL = -15.2733. We next use Excel’s Solver capability by selecting Data > Analysis|Solver. We fill in the dialog box that appears as shown in Figure 2 and then press the OK button.
Figure 2 – Solver dialog box
Results
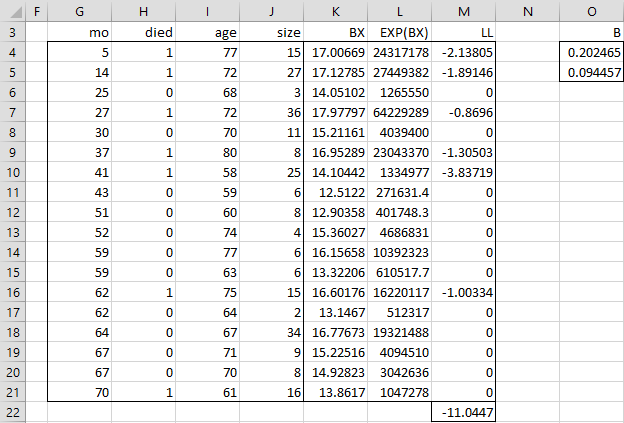
Solver then adjusts the values of the coefficients (range O4:O5) to maximize the value of LL (cell M22). The results are shown in Figure 3.
As we can see, the coefficient corresponding to age is .202465 and the coefficient corresponding to size is .094457. We also see that the value of LL increased from -15.2733 to -11.0447.
Figure 3 – Cox Regression (Solver)
Examples Workbook
Click here to download the Excel workbook with the examples described on this webpage.
References
NCSS (2015) Cox regression
https://www.ncss.com/wp-content/themes/ncss/pdf/Procedures/NCSS/Cox_Regression.pdf
Collett, D. (2003) Modelling survival data in medical research. 2nd ed. Chapman & Hall/CRC
Zhang, D. (2011) Modeling survival data with Cox regression models
https://www.scribd.com/document/396594178
Grund, B., Yang, L. (2015) Hazard regression
https://edoc.hu-berlin.de/server/api/core/bitstreams/595cb9b6-0c1a-4121-8a83-8a194f19b3ae/content
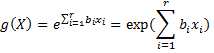
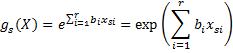
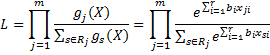
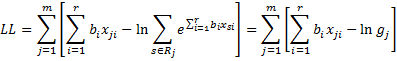
I find your explanation of the Cox PH method very useful. Please send me the spreadsheet in the post which solves the Cos PH method using Excel
Thank you.
Jack Simonis
Jacksimonis@ymail.com
Hi Jack,
Glad to hear that the website has been useful.
You can download any of the spreadsheets from
https://www.real-statistics.com/free-download/real-statistics-examples-workbook/
Charles
Hello Charles,
Your post is extremely helpful!
My one question is how do you get baseline or h0(t)?
JT
Dear Jung,
See https://www.real-statistics.com/survival-analysis/cox-regression/baseline-hazard-function/
Charles
Is the g sub j (X) in the numerator of the partial likelihood function the subject who dies at t sub j? If so, then it will help to mention that explicitly.
Parikshit,
It is mentioned explicitly. See the following three statements on the webpage:
“Dj be the set of all subjects who die at time tj”
“In fact, initially we will assume that dj = 1 for each j.” (i.e. one death in Dj)
“where xji is defined to be xsi where s is the unique element in Dj. Similarly gj(X) is defined to be gs(X) in this case.” (this is where it is stated)
Charles
Charles,
Thanks for posting this excellent resource. It’s very helpful to see things step-by-step. In trying to replicate the above spreadsheet and related outputs I may have stumbled on a small inconsistency in the paragraph below Figure 1. Should ‘=EXP(J4)’ read as ‘=EXP(K4)’ instead? (Since column K contains B(x) whilst L is exponent of B(x)).
Huey,
Glad that you find the posts useful and thanks for finding this error. I have now corrected the referenced webpage.
Your help in making the website easier to read is very much appreciated by me and other users.
Charles
Hi Charles,
Thank you very much, this website was extremely usefull!
BR
Hi Charles,
Excellent blog. I don’t understand things well unless I solve them myself.
I had a question regarding the data. How should I read data from row 6. at the end of month 25 no one died. then what does the age and size correspond to?
Thank you
Akshay
Akshay,
All the rows (for the leftside data) represent patients in the study. This is just the input. See the following webpage for details
https://real-statistics.com/survival-analysis/kaplan-meier-procedure/kaplan-meier-overview/
The middle section of the figure represents the same input data in sorted order.
Charles
Dr. Buenas noches, espero se encuentre muy bien, agradezco mucho su trabajo por facilitarnos esta página realmente útil. Dr no entiendo por que no me funciona la regresión de Box Cox, si trabajo con una varaibel dependinte y una independiente, me informa que debo tener mas de 3 independientes, ubico 3 independientes y sale la expresión #¡VALOR!.
Dr, good evening, I am waiting that you are ok, I am grateful by your page, realy its very util. Dr I do not understand why in Box Cox regression, when I work with one dependent variable and independent variable the Real Statistics inform that is not possible, and when i use more independent variables, Real Statistiscs inform to me #¡VALOR!.
Gerardo,
If you send me an Excel file with your data, I will try to figure out what is going wrong.
Charles
Good mornig, many thanks, please wich emal, I send the data?
Gerardo,
See the following webpage
Contact Us
Charles