Introduction
In multiple linear regression, a residual is the difference between the observed and predicted value of the dependent variable based on observed values of the independent variables. Unfortunately, there is no simple counterpart in Cox regression. Instead, the following types of “residuals” are used with Cox regression for such purposes as identifying potential outliers:
- Cox-Snell residuals
- Martingale residuals
- Deviance residuals
- Schoenfeld residuals
- Scaled Schoenfeld residuals
Cox-Snell Residuals
The Cox-Snell residual at time tk is
As remarked elsewhere, we generally use the Breslow estimate of H0(tk), namely
Martingale Residuals
The martingale residual at time tk is
Thus martingale residuals can take a value between -∞ and 1. A large negative martingale residual indicates a high-risk subject who still had a long survival time.
The martingale residuals sum to zero and in large samples they are uncorrelated with one another and have an expected value of zero.
Deviance Residuals
The deviance residual at time tk is
where sign(c) = 1 if c > 0, sign(c) = -1 if c < 0 and sign(0) = 0. High values of indicate potential outliers. For a model with a good fit these residuals are symmetric around zero but they don’t necessarily sum to zero.
Schoenfeld Residuals
For any subject s who dies at time tj and any covariate xi, we define the Schoenfeld residual (aka partial residual) by
In large samples, these residuals are uncorrelated with one another and have an expected value of zero.
Scaled Schoenfeld Residuals
These are defined by
where d = = the total number of deaths and [cil] is the r × r covariance matrix for the Cox regression coefficients.
You can plot these residuals against time to test whether the proportional hazards assumption holds. If the assumption holds, then these residuals will be randomly distributed about the x-axis.
References
NCSS (2015) Cox regression
https://www.ncss.com/wp-content/themes/ncss/pdf/Procedures/NCSS/Cox_Regression.pdf
Collett, D. (2003) Modelling survival data in medical research. 2nd ed. Chapman & Hall/CRC
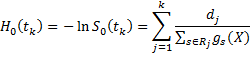
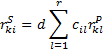
Dear Professor,
To proceed with the test to verify the proportional hazards assumption (see attachment), some authors propose the transformation of times using the “Left-continuous Kaplan-Meier survival function”.
My question is: what is the “Left-continuous Kaplan-Meier survival function”?
But above all, how are event times transformed?
Best regards, Roberto Mioni