The Cox Proportional Hazard Model (aka Cox regression model) is used to analyze the effect of several risk factors (covariates) on survival. The ordinary multiple regression model is not appropriate because of the presence of censored data and the fact that survival times are often highly skewed.
Definition 1: The Cox PH model predicts the value of the hazard function at time t based on the following regression model
Here we consider X = x1, x2, …, xr. These independent variables (aka predictors or covariates) can be categorical or continuous. When the covariates are all zero, i.e. x1 = x2 = … = xr = 0, the hazard function is equal to the baseline hazard function λ0(t). The baseline hazard function depends on t but not on the values for x1, x2, …, xr. The values of x1, x2, …, xr and β1, β2, …, βr are time independent (i.e. they don’t depend on t).
We will use the letters b1, b2, …, br for the coefficients based on a sample and h(t) and h0(t) for the corresponding empirical hazard function and baseline hazard function.
The hazard ratio is expressed as
Note that by taking the natural log of both sides of the Cox regression model equation, we get the multiple linear regression model (without intercept).
Since HR represents the relative risk, we see that the relative risk is independent of the time t (i.e. it is a constant for any specific values of x1, x2, …, xr.). Note that increasing any coefficient by one unit (keeping the other coefficients constant) results in an increase in relative risk. Thus we can think of the coefficients as representing the increase in relative risk due to an increase in the corresponding factor.
Also, H(t) = H0(t) ⋅ exp (
Finally, we see that
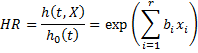
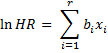
Hello, could you add Weibull PHM?
Many thanks!
Hello Rodrigo,
Thank you for your suggestion. Real Statistics currently supports fitting data with a Weibull distribution including censoring. See https://www.real-statistics.com/distribution-fitting/distribution-fitting-via-maximum-likelihood/weibull-with-multi-censored-data/
This may already provide the support that you are looking for. Please let me know whether there is additional support that you require.
Charles
Thanks for this useful web site and tools. Question: can I use calendar time as a covariate? I am asking if hazard rate is different depending on the dates in which the observation time begins to be measured. I have a dataset in which weekly observations were taken over 4.5 years. First, I calculated Kaplan-Meier S(t) for two periods in the data. Subjects that we began to measure in period 1 median S(t) was 32 weeks while those that began in period 2 median S(t) was 6 weeks. Then I used Cox Proportional Hazards with covariates 0 and 1 for periods 1 and 2, I get beta +1.64 and exp(beta) upper and lower bounds were 4.3 – 6.1. I interpret this as higher risk of an event for subjects starting in period 2 which is consistent with lower median survival. Lastly, I used Cox PH with beginning date as a continuous measure and get beta +0.00622 and exp(beta) 1.001053 – 1.002236 or a 0.1 – 0.2% increase in the hazard per week. Am I interpreting correctly? Thank you!
Peter,
You can use calendar time as the time variable. The date in which the observation started does matter, sort of. Suppose that time goes from 0 to 30 and some observation starts at time 5 and then that subject leaves the system at time 25. You need to rest the times so that the observation starts at time 10 and then the subject leaves at time 30 (i.e. the time when the experiment ends and some subjects, including this one, may not yet have died).
Charles
This blog was very helpful in understanding the concept of Cox regression model.
I am a beginner at Cox regression. Can we have a solved example on to get a better understanding? I have around 6 cardiovascular risk factors. How can i use the Cox regression model to predict the hazard for 10 years?
Ankush,
I am pleased that the blog was helpful. There are examples among the various topic described on the following webpage>
https://real-statistics.com/survival-analysis/cox-regression/
Just click on the topics to see the examples.
Charles
“We performed consecutive Cox’s proportional hazards regression analyses, a first one to fit a null model containing only an intercept parameter (residual x2 (13) 5 22.647, p 5 0.046), which allowed us to select the major parameters of survival;”
What is the intercept in cox proportional regression analysis?
Thank You
Best regards.
Sergio,
As far as I am aware of there is no intercept parameter, however, I guess that the lambda_0 can be viewed as a sort of intercept parameter. In fact, if you set b_0 = LN(lambda_0), you can express the Cox’s proportional hazard regression as exp of the sum of a linear combination of the b_j coefficients, including b_0 (which would be the intercept parameter).
Charles