Assumptions for Two-Sample t-Test

Assumption Guidelines

The two independent sample t-test described above is valid provided the two samples are randomly taken from two populations that are normally distributed with the same variance.

The t-test is quite robust even when the underlying distributions are not normal provided the sample sizes are sufficiently large (usually over 25 or 30 so that the Central Limit Theorem applies). Even for smaller sample sizes, the test is usually valid provided the samples have similar sizes and shapes and are not too skewed.

The test is more robust to violations of normality the larger the sample size, the larger the alpha value, and the more equal the sample sizes are. The test is also quite robust to violations of normality provided the variances are equal.

Even when the variances are unequal, the t-test can be valid, especially when the sample sizes are equal. Also, the larger the ratio between the variances the larger the samples need to be. The test is more robust to a difference between variances when the larger sample has the larger variance.

Equal Sample Sizes

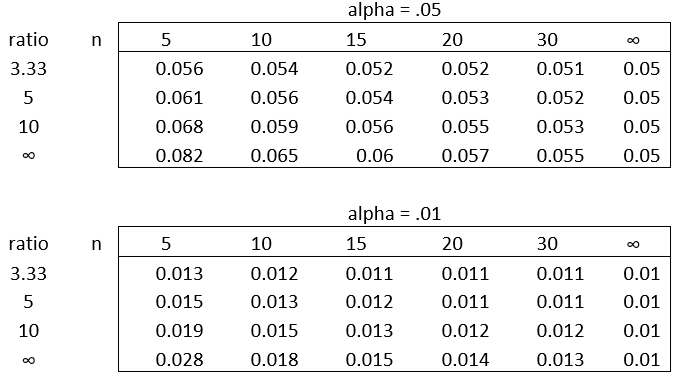
When the sample sizes are equal, the table in Figure 1 shows the real type I error based on the stated two-tailed alpha value, the ratio between the variances, and the sample size n.

Figure 1 – Type I error for equal sample sizes

Unequal Sample Sizes

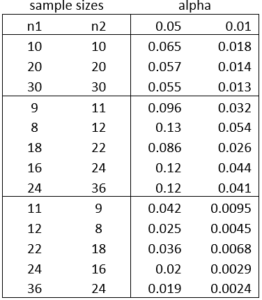
When the sample sizes are different, the discrepancy between the real type I error and the (two-tailed) alpha value increases as shown in the table in Figure 1, where sample 1 contains n1 elements, sample 2 contains n2 elements, and the ratio of the variance for sample 1 divided by the variance for sample 1 approaches infinity.

Figure 2 – Type I error for unequal sample sizes

As you can see from Figure 2, for samples of unequal size the discrepancy between the alpha value and real type I error is much larger than for samples of equal size. Also, the discrepancy is much less when the larger sample has a larger variance.

Dealing with Larger Error

When the samples are normally distributed, or at least not too far from normally distributed, and the variances are unequal, the two-sample t-test with unequal variances should be used. This is especially true when the sample sizes are different.

When the samples are not normally distributed, but the samples have similar shapes and variances, then the Mann-Whitney Test should be used. When the samples are not normally distributed and the samples have different shapes or variances, then you should consider using a transformation.

Reference

Zar. J. H. (2010) Biostatistical analysis 5^th Ed. Pearson
https://bayesmath.com/wp-content/uploads/2021/05/Jerrold-H.-Zar-Biostatistical-Analysis-5th-Edition-Prentice-Hall-2009.pdf