Objective
In Sample Size Requirements for t Tests we show how to determine the minimum sample size for a one-sample t test based on achieving a statistical power objective. There is another way to determine the required sample size, namely by achieving a sufficiently narrow confidence interval.
Example
Example 1: Determine the sample size necessary to achieve a 95% confidence interval for the population mean that is no wider than .5 when the standard deviation of the data is 1.0.
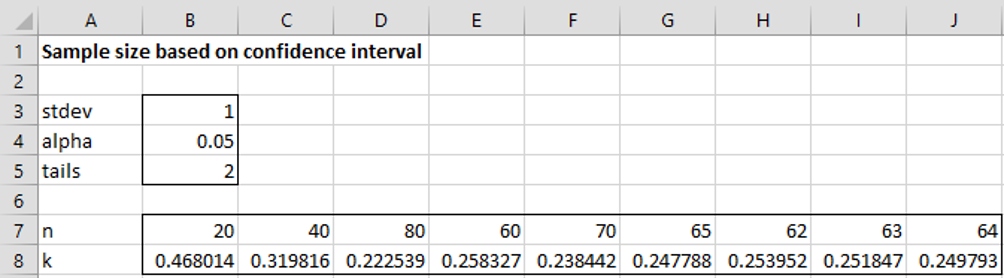
In general, CONFIDENCE.T(α, s, n) = k such that (x̄ – k, x̄ + k) is the confidence interval of the population mean. Thus, we seek the smallest value of n such that CONFIDENCE.T(.05, 1, n) ≤ .5/2. We can use repeated guessing to find this value of n, as shown in Figure 1.
Figure 1 – Finding the sample size
Here, cell B8 contains the formula =CONFIDENCE.T($B$4,$B$3,B7), which we copy to the neighboring cells. We see from the figure that a sample size of 64 is required.
Goal Seek Approach
We can avoid the guessing by using Goal Seek. This is done by selecting Goal Seek from the Data ribbon and filling in the dialog box as shown in Figure 2.
Figure 2 – Finding the sample size using Goal Seek
After clicking on the OK button, the values in cells B7 and B8 change as shown in Figure 3.
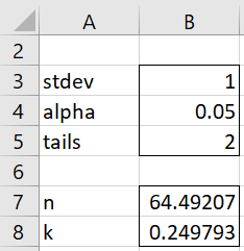
Figure 3 – Sample size results
Rounding up, we conclude that the required sample size is 65.
Note that for a sample drawn from a finite population of size np, especially when the sample makes up a substantial portion of the population, the required sample size n needs to be adjusted to n’ as follows:
![]()
Examples Workbook
Click here to download the Excel workbook with the examples described on this webpage.
Reference
Howell, D. C. (2010) Statistical methods for psychology (7th ed.). Wadsworth, Cengage Learning.
https://labs.la.utexas.edu/gilden/files/2016/05/Statistics-Text.pdf
Zar. J. H. (2010) Biostatistical analysis 5th Ed. Pearson