Basic Concepts
In paired sample hypothesis testing, a sample from the population is chosen and two measurements for each element in the sample are taken. Each set of measurements is considered a sample. Unlike in two-sample hypothesis testing (see Two-sample t-Test), the two samples are not independent of one another. Paired samples are also called matched samples or repeated measures.
For example, if you want to determine whether drinking a glass of wine or drinking a glass of beer has the same or different impact on memory, one approach is to take a sample of say 40 people, and have half of them drink a glass of wine and the other half drink a glass of beer, and then give each of the 40 people a memory test and compare the results. This is the approach with independent samples.
Another approach is to take a sample of 20 people and have each person drink a glass of wine and take a memory test, and then have the same people drink a glass of beer and again take a memory test, after which we compare the results of the two tests. This is the approach used with paired samples.
Advantages
The advantage of this second approach is the sample can be smaller. Also since the sampled subjects are the same for beer and wine there is less chance that some external factor (confounding variable) will influence the result. The problem with this approach is that it is possible that the results of the second memory test will be lower simply because the person has imbibed more alcohol. This can be corrected by separating the tests in time, e.g. by conducting the test with beer a day after the test with wine.
It is also possible that the order in which people take the tests influences the result (e.g. the subjects learn something on the first test that helps them on the second test, or perhaps taking the test the second time introduces a degree of boredom that lowers the score). One way to address these order effects is to have half the people drink wine on day 1 and beer on day 2, while for the other half the order is reversed (called counterbalancing).
The following table summarizes the advantages of testing with paired samples versus testing with independent samples:
| Paired Samples | Independent Samples |
| Need fewer participants | Fewer problems with fatigue or practice effects |
| Greater control over confounding variables | Participants are less likely to figure out the purpose of the study |
Figure 1 – Comparison of independent and paired samples
Obviously, not all experiments can use the paired sample design. E.g. if you are testing differences between men and women, then independent samples will be necessary.
As you will see from the next example, the analysis of paired samples is done by looking at the difference between the two measurements. As a result, this case uses the same techniques as for the one-sample case, although usually, it is easier to use either the paired t-test data analysis tool or the T.TEST worksheet function with type = 1.
Hypothesis Testing
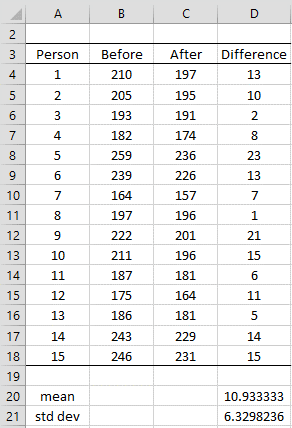
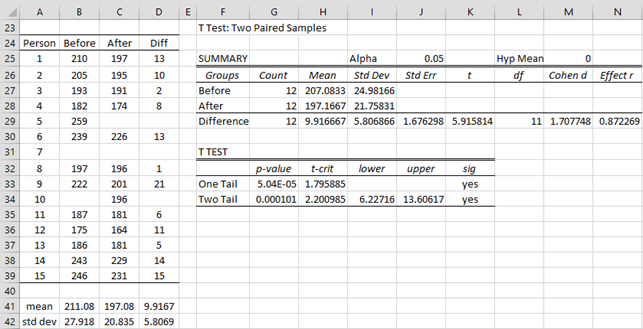
Example 1: A clinic provides a program to help their clients lose weight and asks a consumer agency to investigate the effectiveness of the program. The agency takes a sample of 15 people, weighing each person in the sample before the program begins and 3 months later to produce the table in Figure 2. Determine whether the program is effective.
Figure 2 – Data for paired sample example
Let x = the reduction in weight 3 months after the program starts. The null hypothesis is:
H0: μ = 0; i.e. any differences in weight is due to chance (two-tailed test)
We can make the following calculations using the difference column D:
s.e. = std dev / = 6.33 /
= 1.6343534
tobs = (x̄ – μ) /s.e. = (10.93 – 0) /1.63 = 6.6896995
tcrit = T.INV.2T(α, df) = T.INV.2T(.05, 14) = 2.1447867
Since tobs > tcrit we reject the null hypothesis and conclude with 95% confidence that the difference in weight before and after the program is not due solely to chance.
Alternatively, we can use a type 1 T.TEST to perform the analysis as follows:
p-value = T.TEST(B4:B18, C4:C18, 2, 1) = 1.028E-05 < .05 = α
and so once again we reject the null hypothesis.
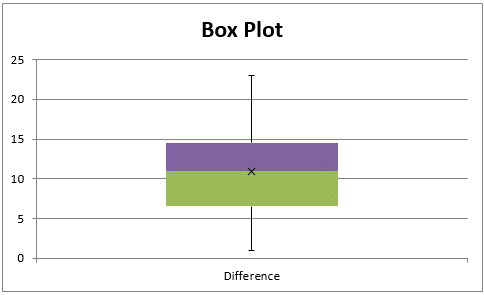
As usual, for the results to be valid, we need to make sure that the assumptions for the t-test hold, namely that the difference measures are normally distributed or at least reasonably symmetric. From Figure 3 we see that this is the case:
Figure 3 – Box Plot for difference measures (column D of Figure 2)
Data Analysis Tools
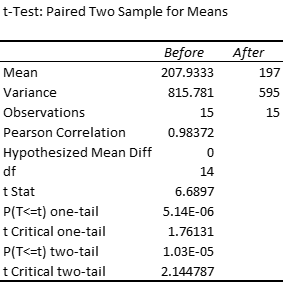
Excel Data Analysis Tool: We can use Excel’s t-Test: Paired Two Sample for Means data analysis tool. The output from this data analysis tool is shown in Figure 4.
Figure 4 – Excel data analysis for paired samples
The Pearson Correlation entry in Figure 4 is explained in Correlation.
Real Statistics Data Analysis Tool: We can also use the T Test and Non-parametric Equivalents data analysis tool in the Real Statistics Resource Pack to get the same result.
To use this tool press Ctrl-m and select T Tests and Non-parametric Equivalents from the menu (or from the Misc tab if using the Multipage interface). A dialog box will appear (as in Figure 1 of t Test Analysis Tool). Enter B3:C18 in the Input Range 1 field (or B3:B18 in Input Range 1 and C3:C18 in Input Range 2) and choose the Column headings included with the data, Paired Samples, and T Test options. When you press the OK button, the output shown in Figure 5 is displayed.
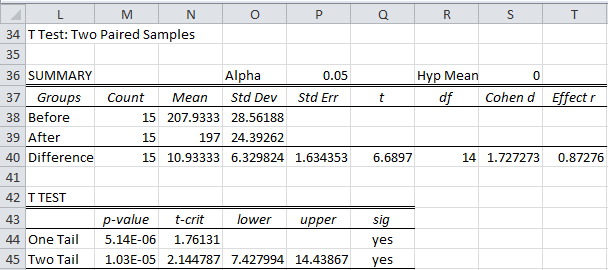
Figure 5 – Real Statistics data analysis for paired samples
Missing Data
The input data for the paired-sample t-test can have missing data, indicated by empty cells or cells with non-numeric data. Such cells will be ignored in the analysis.
Example 2: Repeat Example 1 using the data in range B24:C39 of Figure 6.
In this example, there is missing data for subjects 5, 7, and 10. The analysis is rerun with the data for these people removed. Note that some of the formulas have been changed to account for the missing data. E.g. when there is no missing data, cell H27 can contain the simple formula =AVERAGE(B25:B39), but since there is missing data the following formula is used instead:
=SUMPRODUCT(ISNUMBER(B25:B39)*ISNUMBER(C25:C39),B25:B39)/G27
Figure 6 – Paired t test with missing data
Caution: If you have missing data you can change the data values and even fill in the missing data with numeric values and the resulting analysis will be correct. If, however, the input does not contain any missing data, you can change any of the data values and still get a valid analysis but if you change a numeric value to a non-numeric value then the analysis will not be correct and you will need to rerun the data analysis tool to get the correct results.
Comparing paired samples with independent samples tests
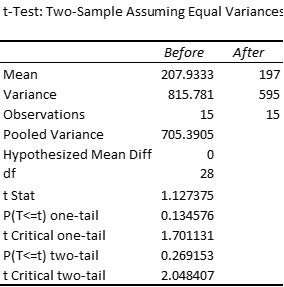
Suppose we run the same analysis for the data in Example 1 from Two Sample t Test with Equal Variances using the t-test with independent samples and compare the results with those we obtained for paired samples:
Figure 6 – Excel data analysis for independent samples
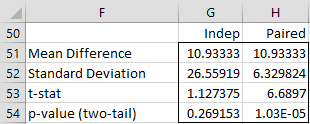
We summarize the results from the two analyses as shown in Figure 7.
Figure 7 – Comparison of paired and independent sample t-tests
Note that the mean differences are the same, but the standard deviation for the paired sample case is lower, which results in a higher t-stat and a lower p-value. This is generally true.
One-sample test
Although Real Statistics provides a data analysis tool for one-sample tests, Excel doesn’t provide a standard data analysis tool for this case. The T.TEST function with type = 1 and the paired samples data analysis tool can, however, be used for the one-sample case by simply creating a null paired sample with all zero data.
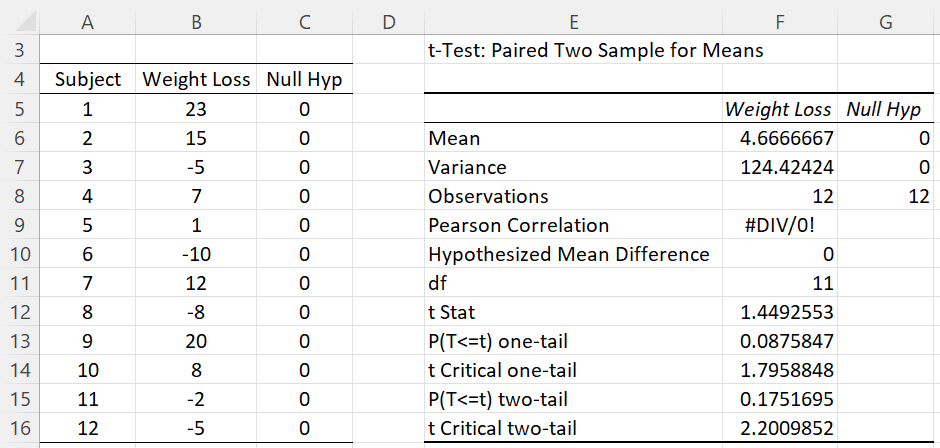
Example 3: Repeat Example 1 of One Sample t-Test using the above observation.
Figure 8 shows how to do this using Excel’s paired t-test data analysis tool.
Figure 8 – Use of paired sample data analysis for one sample test
Effect size
Since the two-sample paired data case is equivalent to the one-sample case, we can use the same approaches for calculating effect size and power as we used in One Sample t Test. In particular, Cohen’s effect size is
where z = x1 – x2. There are other versions of Cohen’s effect size, including drm and dav. These are described at Cohen’s d for Paired Samples.
Examples Workbook
Click here to download the Excel workbook with the examples described on this webpage.
References
Howell, D. C. (2010) Statistical methods for psychology (7th ed.). Wadsworth, Cengage Learning.
https://labs.la.utexas.edu/gilden/files/2016/05/Statistics-Text.pdf
Nelson, S. L. and Nelson, E. C. (2016) How to use the t-test data analysis tool in Excel
https://www.dummies.com/article/technology/software/microsoft-products/excel/how-to-use-the-t-test-data-analysis-tool-in-excel-152093/
Zar. J. H. (2010) Biostatistical analysis 5th Ed. Pearson
Hi Charles,
Thank you very much for your help and resources. It’s been exciting getting started and learning on this amazing program!
I’m following the paired T test tutorial on my Mac, particularly the part about empty cells, but as soon as I try to run the analysis I get an error message that says the 2 input ranges must have the same number of elements. When I run the analysis on a smaller sample without the empty cells it works.
For some reason it seems like the analysis is unable to ignore the empty cells. Do you know of a way to filter out and delete the rows with empty values so I can run the paired T test successfully? It’s a pretty big database to have to go through manually.
Thanks in advance.
Hi Jennifer,
Welcome aboard. Glad to see that you have begun to use Real Statistics.
I will check into the issue of the error message on the paired t-test. In the meantime you can use the Real Statistics worksheet function DELROWS to delete any row that contains an empty cell. You use this prior to running the paired t-test. See the following webpage for details
https://real-statistics.com/descriptive-statistics/missing-data/
Charles
Hello Jennifer,
I have now researched the issues you raised in your comment. I found two problems:
1. There are cases where the software would calculate the t-test correctly but the error message appears because the sample sizes are different. For example
sample 1: 56 x 23 x 12 26
sample 2: 33 2 12 5 15 20
Sample 1 has 4 elements and sample 2 has 6 elements, but two of the elements don’t count. The t-test should be the same as for
sample 1: 56 23 12 26
sample 2: 33 12 15 20
2. The analysis for the Signed Ranks Test for Paired Samples is correct even when the samples are the same size but the medians shown are not correct. For example:
sample 1: 56 x 23 12 26 9
sample 2: 33 2 12 15 20 x
I plan to fix these errors in the next release of the software.
Thanks again for bringing this to my attention. For now, you can eliminate blank rows as described in my previous response to avoid the issue.
Charles
Hello Charles,
I’m trying to confirm that I’m thinking correctly in using a paired samples t-test (and not independent samples) in the following scenario: I’m trying to compare the total return of an unadjusted portfolio to that of a back-adjusted portfolio (based on a constituent weight limit adjustment) when the data points for each sample are the individual weekly returns over a period. Since the adjusted portfolio is an adjusted subset of the original unadjusted, I was thinking these would be paired samples? The single linked total return values for each sample are very different, and the paired sample t-test shows a significant difference, while the independent samples t-test shows p-values in the 0.3 or higher range.
Thanks so much!
Hello Brister,
If I understand things properly, you have two samples with numeric values X = x1, x2, …, xn and Y = y1, y2, …, yn.
In order to use the paired t-test, the following conditions must be met:
(1) both samples have the same number of elements.
(2) you can pair the two samples as follows (x1, y1), (x2,y2), …, (xn,yn) such that for any pair xi and yi refer to the same subject (an element in the portfolio in your case). E.g. xi is the value unadjusted and yi is the value adjusted. The important thing is that xi and yi refer to the exact same subject.
Charles
HAI, I am gonna check the pre and post-sprint of sports athletes, in between I am giving some training intervention. my null hypothesis that intervention will not cause any difference and alternate hypothesis is cause any difference. My major doubt is, I wanna do (a pre-post) test or (a post-pre) test? If I do (pre-post) my values are coming in positive significance but in (post-pre) values are coming in negative value. I hope you will clarify my doubt as soon s possible with a clear explanation.
Hello Arun,
The results of the test will be the same whether you use pre-post or post-pre.
Charles
Hello Charles,
I am running a comparison between impairment expense (seen in the audited financial statements) of blue chip companies, before and after adoption of a new accounting pronouncement.
Given that each blue chip company may have different amounts of impairment (one is about $300K and the other is about $10.4 million). What I was thinking is to use the paired t-test sample, but instead of using the dollar value of impairment, I will convert the dollar value and express it as a % (i.e., impairment expense over total sales or net income, whichever has higher correlation).
The paired t-test will be on the blue chip companies on their percentage expressed means (i.e., impairment expense over total sales or net income, whichever has higher correlation) before and after the introduction of the new accounting pronouncement. Does this pass the sanity test?
Business student here, working on a research project. Appreciate your thoughts and the write-up made on the paired t-test.
Thanks.
Jason
Hi Jason,
This seems to make sense, although I haven’t thought about it in detail. You will be comparing the percentage of impairment before vs. after. You still need to make sure that the assumptions for the paired t-test are met.
Charles
Hello Charles,
I have to run a T-Test for a single flight experiment conducted on two groups of butterflies. The sample size is same for both groups, would a T-Test be acceptable? And would it be paired or two-sample, and one tailed or two tailed?
Hello Rehnuma,
If you are trying to compare two independent groups of butterflies, then the two-sample t-test is appropriate (provided the assumptions for the test are met). Usually, the two-tailed test is used, but this depends on the hypothesis that you are trying to test.
Charles
Hi pls help me with this question ❓ plan simple experiment for tests concerning one mean
Hi Mary,
What is your question?
Charles
Hi Charles,
I am comparing two groups, Pre and Post, The pre-group consists of two years like 2015, 2016 while the post group consists of 2017,2018, and 2019. Two years before and 3 years after with 100 sample companies. Variables remain the same like board size before and after. As per literature paired sample t-test is used, but here I cannot make separate the groups because pre consists of 2 years and post 3 years and the variables inside them.
like board size for 2015 and 2016 and comparison with the board size of 2017,2018,219, while I am considering them two groups.
Hi Fayaz,
If you are only interested in comparing Pre with Post, one approach is to take the average of the data for 2015 and 2016, and compare it with the average of the data for 2017, 2018 and 2019. If you are interested in the comparisons year to year, you might use repeated measures ANOVA (or MANOVA).
Charles
Hi sir
I have to determine whether the two methods of teaching online and offline are stastically different. For this I have taken a class of 50 and divided the students into two equal groups of size 25 each. Which type of t-test should I use to determine whether the two methods yield different results. My variable for comparison is knowledge score/ marks scored in an exam
Hi Irfan,
If I understand the scenario correctly, this looks like a fit for the two independent sample t-test.
Charles
Dear Charles,
If I do both a pretest and posttest on an intervention group and a control group. How do I best analyze if the intervention group increased their scores more than the control group? Do I perform separate t-tests on both groups pre and post results or do I do an ANOVA? Sorry, I’m new to analyzing statistics.
Dear Karin.
This is an excellent question. See the following webpage which explores this issue:
https://www.real-statistics.com/analysis-of-covariance-ancova/pretest-posttest-design/
Charles
Sir I am comparing five years ‘A’ mutual fund daily returns with its five years benchmark (index) returns, means one mutual fund is compared with one index for their five years.
Can I use paried sample text?
If you are comparing two years then a paired sample t-test could be appropriate. With 5 years you need to use Repeated Measures ANOVA. See
https://www.real-statistics.com/anova-repeated-measures/
Charles
In place of daily returns, if I compare yearly returns of mutual fund and benchmark for 5 years, then can paired sample t test be used.
Is the benchmark a single number or is there one value for each of the 5 years?
If the benchmark is a single number then the one-sample t-test is appropriate, while if there a benchmark for each year then the paired t-test is appropriate (assuming the test assumptions are met).
Charles
Hi,
If I compare Mutual fund ‘A’ yearly return with its benchmark index yearly return and with other mutual fund yearly returns than should I use paired sample t test with following pairs:
1) Mutual Fund A return – benchmark index return
2) Mutual fund’A’ return- Mutual fund ‘B’ return
3) Mutual fund’A’ return-Mutual fund’C’ return
Can in this manner pairs can be compared?
Or if not than what should I use to do so?
Hi,
If I understand your examples correctly, then (1) uses a paired t-test, while (2) and (3) use the two-sample t-test.
In all cases, the assumptions must hold (esp. normality), otherwise, you need to use the non-parametric equivalent test.
Charles
Hi Charles,
A group of 60 students were surveyed on their scores before and after anti addiction policy was introduced. (Control on time spent playing video games from being unlimited to 2 hours on week days) I have scores of same set of students before and after. I need to find if the time ban really helped in improving the scores.
Can I do a paired t test on a sample of 10 students scores before and after the ban to check if introducing the policy made a change on their scores or not ?
Thanks
Hi Diya,
Yes, you can use the paired t-test for this purpose.
Charles
Hi can you help me regarding what tests can be used with one sample to find post intervention effects?
Hello George,
If the normality assumption is met, then the paired t-test is a good choice. Otherwise, you could use the Wilcoxon signed-ranks test. The last resort is the signed test. All these tests are covered on the Real Statistics website.
Charles
Hi
I really need help , because I’m not really sure if my answer coming from excel is correct , I got this result from mine data and I really don’t know run through scientific notation
1.31E09
Hello Maybel,
1.31E09 is equivalent to 1,310,000,000 (i.e. 1.31 billion)
Charles
Hello charles
I m doing a research on does yoga exercise reduce eye fatigue by using questionnaire i have 2 groups exercise n control (30 in each) each groups tested before(baseline score)n after8 week score & patients are also segregated into category acc. To score : normal(0), mild(1-24),moderate(25-48),severe(49-72) both in before n after
Now i have to check whether there is statistical difference in excercise n control grp baseline score categories and after 8 weeks categories i think independent t test will be used BUT how to make columns n row
I hope u understood my problem and solve it too!
Thank you in advance
Saima,
With pre- and post-treatment data for two groups, you have a few choices for how to perform the analysis. Which approach to use can depend on the specific hypothesis or hypotheses that you want to test. In general, you could use a paired t-test (if you don’t care about the control group) or a two-sample t-test (if you only care about the difference between the pre- and post-treatment scores). You could also use a repeated measures ANOVA (with both within and between subjects effects) or an ANCOVA. See the following webpage for an explanation:
https://www.real-statistics.com/analysis-of-covariance-ancova/pretest-posttest-design/
Charles
hi Charles, thank you for this informative article. I am investigating whether there have been changes in the hours of exercise completed in my sample before vs after lockdown. here is my data:
hours : before , after
0-2 : 4 , 3
3-5 : 1 , 7
6-8: 5 , 2
9-11 : 2. , 0
12+: 0 , 0
this is the result I got from excel:
t-Test: Two-Sample Assuming Unequal Variances
Variable 1 Variable 2
Mean 2.4 , 2.4
Variance 4.3 , 8.3
Observations 5 , 5
Hypothesized Mean Difference 0
df 7
t Stat 0
P(T<=t) one-tail 0.5
t Critical one-tail 1.894578605
P(T<=t) two-tail 1
t Critical two-tail 2.364624252
im not sure if this is correct. what have I done wrong and how should I go about approaching this data set to calculate the t test as I want to see if there is a statistically significant difference.
thank you!!
Hi Mel,
I am trying to figure out what your data represents. Are you saying that you have two independent samples each with 12 subjects and “3-5: 1, 7” means that prior to lockdown only one person in the pre-group did 3-5 hours of exercise, but 7 of the 12 people in the post-group did 3-5 hours of exercise? In this case, you need to use the two independent sample t-test (presumably using the midpoint of the range, 4 in the case of the 3-5 interval). Better yet, you could use the chi-square test, but since some of the values are zero, you would use the Fisher Exact test instead.
To use the paired t-test you need to have only one group (presumably of size 12) and for each person in the sample, you would need to know the number of hours of exercise pre and post. I don’t see this information in the data that you have provided.
Charles
sorry if my data wasn’t clear – for example for 0-2 hours, 4 people did this much exercise before lockdown and 3 did that much after lockdown, then for the next row 1 person exercised 3-5 hours before, and 7 people exercised 3-5 hours after lockdown etc.
the questions I asked was ‘how many hours of exercise did you do before lockdown?’ and then how many hours of exercise did you do after lockdown?’ – and the data represents the answers to these two questions.
so would you recommend I do the two independent sample t-test or the fisher exact test? I have never done the fisher exact test before so im not sure which test would be the most appropriate.
thank you in advance!
also, wouldn’t the fisher exact test not work as it is only for 2×2 contingency tables, but I have 5 categories for the hours of exercise completed?
Mel,
You can do the Fisher exact test with contingency tables that are not 2×2. See
Fisher Exact Test
Charles
Mel,
In this case, you did collect data pre and post-lockdown for all 12 subjects in the sample. The problem is that you didn’t present the results in a usable format. The way you presented the data you lost the link between pre and post-lockdown for each of the 12 subjects.
You need to present 12 rows, representing the 12 subjects. For row 1 you provide two values: the hours pre-lockdown and the hours post-lockdown for subject 1. You provide similar information for all 12 subjects.
Now you can perform a paired t-test using the mid-points of the intervals (e.g. 3-5 takes the value 4). This approach is valid provided the paired differences are normally distributed. If not, then you can use the Wilcoxon Signed Ranks test.
You could perform Fisher’s exact test, but in this case, each of the intervals would be treated as categorical and so you would lose the information that 6-8 is better than 3-5 and 3-5 is bigger than 0-2. This is not so desirable.
Charles
thank you so much for your response, I see where I went wrong now,
could you please clarify what you mean when you say that performing the paired t-test using midpoints is valid but only if the paired differences are normally distributed?
thank you!
Mel,
These are two separate ideas.
1. Since you have intervals, you need to decide on a single value that represents the interval. The midpoint is a reasonable choice. This assumes that the data for each interval is symmetrically distributed within the interval.
2. A requirement for the paired t-test is that the paired differences be normally distributed. The t-test is pretty robust to violations of this assumption.
Charles
how do I see if my data is normally distributed?
You can use the Shapiro-Wilk test or a variety of other approaches as described at
https://www.real-statistics.com/tests-normality-and-symmetry/
Charles
Hi I am in desperate need of help. I just can’t understand this at all. Would someone be happy to help?
Hi Sue,
What sort of help do you need?
Do you have some specific questions?
Charles
Hi, I’m doing a dissertation and I can’t understand the results and how to explain them. My supervisor has done a chart for me but I don’t understand how to interpret it.
Sue,
Is there any way for you to narrow in on the specific issues that you are having problems with? Otherwise, I can only suggest that you read the Paired t test webpage.
Charles
Hello Charles,
Thank you for the article, can I have some advice on my work? I was asked to carry out a two-tailed t-test to determine whether the concentration of a sample differ from a certified material. I was also provided with an equation – [tcal = (ẍ – µ) √n/s], in which µ is the certified concentration. The problem is that the certified material has a ranged concentration (e.g. 38.63 ± 0.62), how should I apply the t-test?
Thank you for your time.
It depends on how I should interpret 38.63 ± 0.62 and what the value of the sample size n is. If 38.63 ± 0.62 is the confidence interval, then you can use the formula for the confidence interval to find the mean and standard deviation. In any case, the confidence interval will tell you the results of the t-test.
Charles
Thanks for your reply.
I have 4 concentration values from the same sample, and I was told the true value for the concentration is 38.63 ± 0.62, meaning it could be any numbers between 38.01 to 39.25; then I have to carry out a t-test with the null hypothesis being ‘there is no significant difference between the concentrations of the samples and the true value’ – to prove the obtained data is accurate.
I’m not sure how to calculate the interval confidence you have mentioned.. Thank for so much for your help
Andrea,
See https://www.real-statistics.com/students-t-distribution/one-sample-t-test/ regarding the confidence interval.
Charles
Hello Charles,
I am wanting some advice on the TTest for some pollution data
The data is 2019 vs 2020 pollution data. For the same time period.
How would you suggest I go around doing the TTest for this?
Thank you
Cerys,
What hypothesis are you trying to test?
What sort of pollution data do you have?
Charles
is paired t test can be use for 2 set of results obtained from original and duplicate samples?
Yes, if by a duplicate sample you mean that the same subjects as in the original sample were used.
Charles
one doubt I am having regarding the application of paired t-test. I have to compare pre-merger and post-merger financial performance of SBI through different ratios. Merger of associate banks into SBI happened during 01 April, 2016 to 31st March, 2017 (2016-17). Post-merger, I have taken data of 2017-18, 2018-19 and 2019-20 and pre-merger I have taken data of 2013-14, 2014-15 and 2015-16 and have left the year of merger, i.e. 2016-17.
Here, the problem I am facing is how to pair data in SPSS, like
1.
2013-14—-2017-18
2014-15—-2018-19
2015-16—-2019-20;
Or,
2.
2013-14—-2019-20
2014-15—-2018-19
2015-16—-2017-18.
In 1 above, the pairing is in a sequence like first year of available data (2013-14) has been paired with the data of first year after merger (2017-18), second year with second year after merger and so on. In 2 above the pairing is done like 3 years before merger (2013-14) with 3 years after merger (2019-20), 2 years before merger with two years after merger and one year before merger with one year after merger.
Though the mean is same in 1 and 2 above but the SD is different. Kindly suggest me whether to choose 1 or 2 above.
This depends on what specific hypothesis you are trying to test.
Note, however, that you can’t mix multiple pairings for the same company. E.g. if for company XYZ you have data for one year pre- and post-merger as well as two-years pre- and post-merger, you can’t use both pairs since this would violate the assumption of random, independent data in each sample (i.e. you can’t have two data elements from the same company in each sample).
Charles
Hi,
I am comparing data on a pre- and post- test for the same group of students to see if an activity we did increased their knowledge on a topic. However, the tests were anonymous so I can’t match up each individual student’s pre- and post- test. About 100 students took the pre-test and only 65 completed the post-test. They answered 20 different questions on the topic. What’s the best way to approach the stats to determine whether they learned something?
Thank you
Katie,
It seems like you are confronted with how to perform a statistical test after a poor design. Some sort of code needed to be used that was not linked to a name, but the same code was retained from pretest to postest phase. In this way, a paired test would have been possible.
About all you can do now is to perform a two-sample t-test, although the assumptions for this test are violated, I wouldn’t be that confident about the meaningfulness of the results.
Charles
Thank you, Charles. That’s what I was afraid of. One final clarification: would it be inappropriate to compare the average student score on question 1 pretest vs. question 1 post-test, question 2 pre- vs. post, etc. using the paired T-test or some other analysis?
Katie,
If say you had 10 questions and for each question, you had the average score pre-test and the average score post-test, then I believe that you are suggesting to use a paired t-test (with a sample of 10 pairs) to test the hypothesis that the average score didn’t (or did) change. This seems like a reasonable approach, although it suffers from the drawback that the samples are not independently drawn. In fact, it is likely that the average scores between questions are correlated.
Charles
Subject
1
2
3
4
5
6
7
8
9
Before
312
242
340
388
296
254
391
402
290
After
300
201
232
312
220
256
328
330
231
What is your question?
A clinic provides a program to help their clients lose weight and asks a consumer agency to
investigate the effectiveness of the program. The agency takes a sample of 15 people, weighing
each person in the sample before the program begins and 3 months later. Determine whether
the program is effective.
Null hypothesis:
Alternative hypothesis:
Person Before After D D²
1 210 197
2 205 195
3 193 191
4 182 174
5 259 236
6 239 226
7 164 157
8 197 196
9 222 201
10 211 196
11 187 164
12 175 181
13 186 231
14 243 229
15 246 231
Computation for 𝑡.
Decision:
Conclusion:
What is your question?
Charles
May i ask favor how to solve thes problem?
Chrizel,
Is this question directed to Fatima or to me?
Charles
Can yiu give me a online tools for our activities.
Fatima,
You can perform a paired t-test using Excel’s Data Analysis tool. You can find this tool on the Data ribbon.
Charles
Hi George- I am comparing customer satisfaction scores pre and post an intervention. Is the two-tailed t test appropriate? The sample sizes are similar in the pre group and post group. The intervention was nursing report being moved to the bedside.
Ann,
Are the pre-intervention and post-intervention groups different (in other words you have control and treatment groups)? If so, then a two-sample t-test is appropriate if the assumptions for the test are met.
Charles
Hi George- I am comparing customer satisfaction scores pre and post an intervention. Is the two-tailed t test appropriate? The sample sizes are different in the pre group and post group. The intervention was nursing report being moved to the bedside.
Hello Ann,
Are the pre-intervention and post-intervention groups different (in other words you have control and treatment groups)? If so, then a two-sample t-test is appropriate if the assumptions for the test are met.
Charles
Hello Charles,
I want to find the significant difference in the acceptability of the proposed intervention as assessed by two groups. My sample size for the first group is only 10, while the second group consists of 20. Would it be correct to use paired t-test for this?
Alyssa,
No. With two groups you would use the two-sample t-test.
Charles
Dear Charles,
Looking at the covid stats in US using PCA, low correlations but clearly show difference between W, A-America, Hispanic via poverty levels per state.
I calculated a pre (expect infection level) and post(actual level) based on the proportions I obtained, I ran paired t-test using actual population values per state and calculating the difference.
Applied a t-test – obs > critical at 95%, so there appears to be a significant difference.
The differences in theory need to be normally distributed, I have not yet checked, but I am wondering if you think this is a valid approach.
This seems like a reasonable approach if you are comparing before vs after for any specific population (e.g. poor people in the US). If you are comparing one population with another (e.g. North America vs Latin America) then you need to use a different test: two-sample t test or perhaps two-sample proportion test.
Charles
Hi Charles,
I am using your excel package would like to do a paired t test on pre and post test data from the same participants. However, I’m not sure whether I should put the pre test data as input 1 or input 2, as reversing the order gives slightly different statistics.
From your screenshots, I see you do input 1 as the pre test/before; is there a specific reason why? Because usually it seems that running these tests, we do post – pre, instead of pre – post.
Thank you in advance! Also, thank you for making a fantastic excel add-in.
Sam
Hi Sam,
The order should not matter.
Glad that you are getting value from the Real Statistics add-in.
Charles
Thank you. Another question.
How can you calculate the confidence interval for a paired t test and a wilcox signed rank test using the real statistics pack in excel?
1. This webpage gives an example of the confidence interval for the paired t-test.
See the following webpage regarding the confidence interval for the one-sample t-test. This is relevant since the paired t-test is a one-sample t-test where the data is the differences between the pairs.
https://real-statistics.com/students-t-distribution/one-sample-t-test/
2. See the following webpage regarding the confidence interval for the signed ranks test.
https://real-statistics.com/non-parametric-tests/wilcoxon-signed-ranks-test/signed-ranks-median-confidence-interval/
Charles
Hello,
I am trying to figure out the best statistical analysis to use on two sets of data:
1. Each patient had an ultrasound done by hospitalist and then by radiologist. Want to compare the mean time for ultrasound done by hospitalist vs radiologist to see if there is a difference. I am assuming normal distribution as n=50. What type of t-test do I use? paired vs unpaired, two taile vs 1 tail, type 1, 2, or 3?
2. Pretest and post-test scores. best to use ANOVA?
thank you very much
Hello Priyanka,
1. If the same patients are having their ultrasounds done then you should use a paired t test
2. For pre-test vs post-test you should again use a paired t test. You need ANOVA if you have multiple factors or more than two samples.
Charles
thank you for the response. In the same vein:
Patients are getting an ultrasound by radiologist and by hospitalist. i am comparing the time it takes radiologist vs hospitalist to complete an ultrasound. My sample size in <30. I performed a shapiro wilk test that showed that the data was not normalized. So i have to do a non parametric study to compare the mean times and see if there is a difference. Which test is most appropriate?
If the same patients are being tested by both the radiologist and hospitalist, a Wilcoxon Signed-Ranks test is probably the way to go. This test tends to be used to test the median and not the mean (provided the assumptions are met).
If the differences are normally distributed then you should use a paired t-test instead.
Charles
understood. So i should do a shaprio wilk test to see if the differences are normally distributed, correct? I cannot seem to get a wilcoxon signed -ranks test to work in excel.
Hello Priyanka,
Yes, that is correct. You need to perform Shapiro Wilks on the differences.
Wilcoxon Signed-Ranks Test is provided by the Real Statistics add-in to Excel. Do you have this add-in installed?
Charles
More and more I’m confusing myself. I’m trying to figure out how to set up analysis for two groups (intervention and control) who each took two tests (immediate and delayed). Ultimately, I want to find out if the intervention group scores are significantly higher on both the 1st and 2nd tests and if there is any statistical difference between the two. My sample size if relatively small, but equal with n=11 for both groups. Using Excel 2013
Mel,
The reason that it is confusing is that you have two factors: Group (intervention vs. Control) and Test (Immediate and Delayed). The subjects for the first factor are different, but the subjects for the second factor are the same. You could perform two tests, a two independent sample t test for the for the first factor and a paired t test for the second factor. If, however, you are interested in the interaction between these two factors, then you can conduct a repeated measures ANOVA as described at
One between subjects factor and one within subjects factor.
Charles
hi.
I need to compare water quality parameters during wet and dry season. i know i should run paired sample t-test.
But, number of data between wet and dry seasons are not the same. what should i do?
what i did, i tried run two sample sample t-test instead of paired t-test. is it wrong? can u please suggest me what is the right way to get an accurate answer? thank you
Probably two sample t test is correct, but I would need more information to say for sure.
Since wet and dry seasons are different, it is unlikely that a paired t test would be correct even if the sample sizes were the same.
Charles
i took wet and dry season’s data at the same one sampling point.
Hello Mun,
Thanks for your response.
What do you mean by “the same sampling point”?
Why are the number of samples for the wet and dry seasons different?
Charles
i took the data at the same point throughout the may-oct 2018 skip november (bcs of technical problem) and continue in dec until april 2019 which dry season(may-sept) wet( oct -apr) . so basically i have 5 months in dry season and 6 months in wet season.
Thanks. The sample isn’t really random since you are probably taking the data at the same place for all 11 months, but otherwise it looks like a fit for a two-independent sample t test. You only have small samples and so power will be quite low.
Charles
Hi, can you confirm that testing for homogeneity of variance is not required in a paired t test as they are the same sampling group. Thanks
Hello Lucie,
I confirm that you don’t need to worry about homogeneity of variance for the paired t test.
Charles
please help regarding my study on breast cancer cases. i took 102 total pts suffering from breast cancer and presence of metastasis in them. 55 pts do not take tobacco and 2 had metastasis ,47 pts. take tobacco and 10 had metastasis in this group.
Q. which test is best to apply in this case?
Q. will p value give the best result about significant association?
Q. shall I find correlation , in this case?
Q. what is the method to find correlation?
Q. Please explain how to apply ttest in excel for this scenario, as I have done it but still not confident about the p value result.
thank you in anticipation
Hello Anuj,
1. The chi-square test for independence is the usual test, however note that since one of the cells will contain a value less than 5 (namely 2), you should use the Fisher Exact Test. See
https://real-statistics.com/chi-square-and-f-distributions/independence-testing/
https://real-statistics.com/chi-square-and-f-distributions/fishers-exact-test/
2. Yes, the p-value will determine whether there is a significant association
3. You don’t need to find the correlation, but you can
4. See https://real-statistics.com/chi-square-and-f-distributions/effect-size-chi-square/ for how to determine the correlation
One final note: These tests are related to testing the correlation as well as the t test. See
https://real-statistics.com/correlation/dichotomous-variables-chi-square-independence-testing/
Charles
Thank you
Hello guys! I need help with my study. I did a research pretest and post test type using likert scale questionnaire. I used the same questionaire and same respondents from pre test to post test. I did 3 post test at 2 weeks interval for each post test( after their participation to the treatment). I dont know what statistical tool to analyze my data. Any input will be highly appreciated. Thank you
Hello Nerel,
Before you decide on the statistical test to use, you need to decide what hypothesis or hypotheses you want to test.
What hypothesis or hypotheses do you want to test?
Charles
Thank you for the reply. We want to determine if their participation in the treatment has an impact on their answer to question #1 to 5 or if their answer is similar over time from pre test to post.
1. For each question you can perform (a) a paired t test to compare pre with post results for that question in the treatment group and (b) a two sample t test to compare the treatment group with the control group. Since you are performing multiple test you need to take familywise error into account.
2. For each question, you can combine (a) and (b) in approach 1 and use a repeated measures ANOVA with a between subjects factor (pre vs post) and a between subjects factor (group vs treatment)
3. You can perform approach 1 across all 5 questions by using (a) a paired Hotelling’s T-square test for pre vs post and (b) a two sample Hotelling’s T-square test to compare the treatment vs control group
4. You can perform approach 2 across all 5 questions by using MANOVA with one within subject factor and one between subjects factor.
Charles
hello
can you please do me a favor?
will you calculate the paired T test for the following data?
pre test post test
17 29
20 31
15 32
27 25
26 26
22 24
24 24
14 34
19 24
22 36
21 25
19 29
25 29
16 26
12 40
16 33
22 28
20 33
23 35
22 31
21 33
17 29
12 32
18 21
19 24
19 27
19 33
21 26
15 29
9 32
This webpage shows how to carry out the test.
Charles
Hello,
I am comparing answers of two surveys, given to the same set of subjects, 10 years apart. I have 20 subjects, and each survey has 37 questions. I am not necessarily looking for the difference between subjects responses, rather if the survey answers are reliable or similar over time. I can’t decide if a paired sample t-test or Cohen’s kappa is more appropriate?
Appreciate the help!
Rebecca,
You can use Cronbach’s alpha to determine whether the survey is reliable and the paired t test to determine whether the answers are similar.
Charles