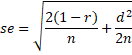Cohen’s d for Paired Samples

d_z effect size

Since the two-sample paired data case is equivalent to the one-sample case, based on the differences between the sample elements, we can use the same approach for calculating the effect size, statistical power, and sample size as we used in One Sample t Test. In particular, Cohen’s effect size is

This is equivalent to

where z = x₁ – x₂.

This version of Cohen’s effect size is useful for estimating statistical power and sample size, but it is not the most commonly used version of Cohen’s effect size for paired samples.  Instead, we use d_rm (Cohen’s effect size for repeated measures) or d_av (Cohen’s d using an average variance).

d_rm effect size

The formula for the first of these is:

where

and r is the correlation coefficient between x₁ and x₂, as described in Correlation Coefficient. r can be calculated in Excel by the formula =CORREL(R1, R2), where R1 and R2 contain the sample data. Note too that

d_av effect size

The formula for d_av is

where

Between d_rm and d_av, the second is preferred since its values can more easily be compared to Cohen’s d for two independent samples, i.e. we can determine whether the effect measured in an experiment with paired samples (e.g. pre-treatment vs. post-treatment) is higher or lower than the effect measured in an experiment with two independent samples (e.g. with separate treatment and control groups).

Hedges’ g

As in the one sample and two independent samples cases, the above versions of Cohen’s effect size are slightly biased, especially for small samples. Once again we can obtain a less biased statistic, called Hedges’ g, defined as follows (where d is any of d_z, d_rm or d_av). This time, g_rm and g_av are not completely unbiased, but they are less biased than d_rm and d_av.

where df = n – 1 and m = df/2.

Confidence intervals

In the literature, you will find the calculation of a confidence interval for Cohen’s d_rm as d_rm ± se · z_crit using the following estimate of the standard error of d_rm.

We won’t pursue this further since the theoretical grounds for this approximation are not clear, and anyway, we prefer using d_av. The above estimate is reasonable for

where s₁ is the standard deviation of one of the samples.

A confidence interval for d_z can be computed as described in One Sample Effect Size. The calculation of a confidence interval for d_av is described in Confidence Intervals for Effect Size and Power.

References

Hedges, L. V. and Olkin, I. (1985) Statistical methods for meta-analysis. Academic Press
https://www.academia.edu/17621684/Statistical_Methods_for_Meta_Analysis

Enzmann, D. (2015) Notes on Effect Size Measures for the Difference of Means From Two Independent Groups: The Case of Cohen’s d and Hedges’ g
Available via Researchgate