Definition 1: x has a non-standardized t distribution (aka a three-parameter t distribution), denoted x ∼ T(ν, µ, σ), when
The standardized version of this distribution, T(ν, 0, 1), is the usual t distribution T(ν).
Here, ν > 0 is the degrees of freedom (or shape parameter), µ is the location parameter and σ is the scale parameter.
The cdf of the non-standardized t distribution can be calculated in Excel by the formula
=T.DIST((x–µ)/σ, ν, TRUE)
The pdf can be expressed in Excel by
=T.DIST((x–µ)/σ, ν, FALSE)/σ
The inverse function can be expressed in Excel by
=σ*T.INV(p, ν)+µ
Observation: Key statistical properties of the non-standardized t distribution are shown in Figure 1.
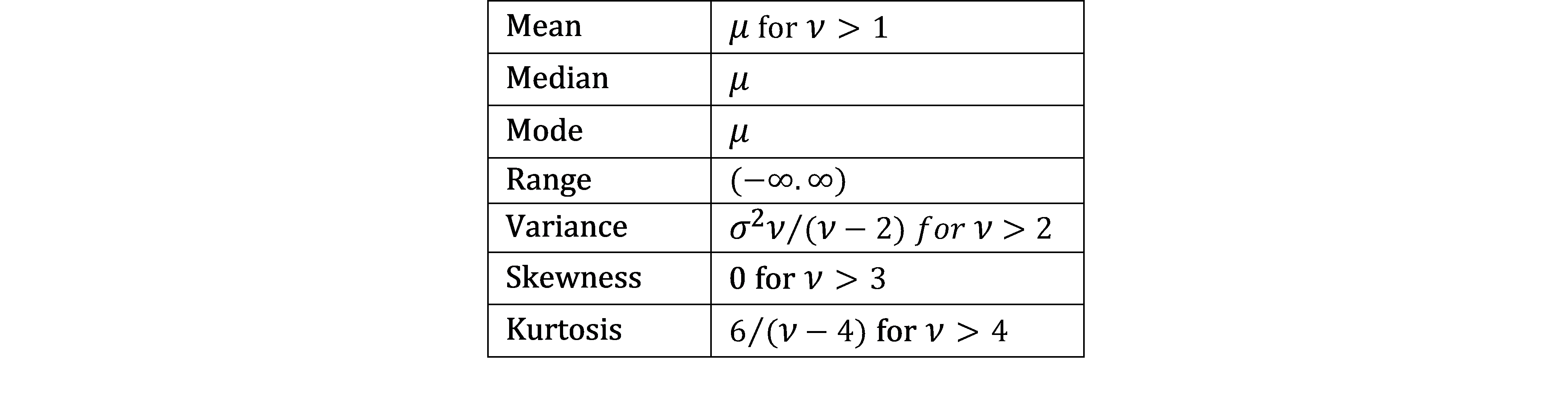Figure 1 – Key statistical properties
Real Statistics Functions: The Real Statistics Resource Pack provides the following functions for the three-parameter t distribution where df > 0, σ > 0, and cum = TRUE or FALSE:
T3_DIST(x, df, μ, σ, cum) = the probability density function value f(x) for the three-parameter t distribution T(df, μ, σ) when cum = FALSE and the corresponding cumulative distribution function F(x) when cum = TRUE.
T3_INV(p,df, μ, σ) = the value such that T3_DIST(x, μ, σ, TRUE) = p, i.e. inverse of T3_DIST(x, df, μ, σ, TRUE).
Reference
Wikipedia (2020) Student’s t-distribution