Shapiro-Wilk Tables

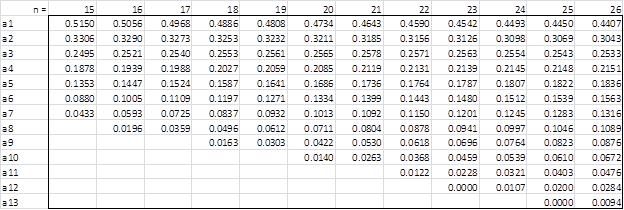
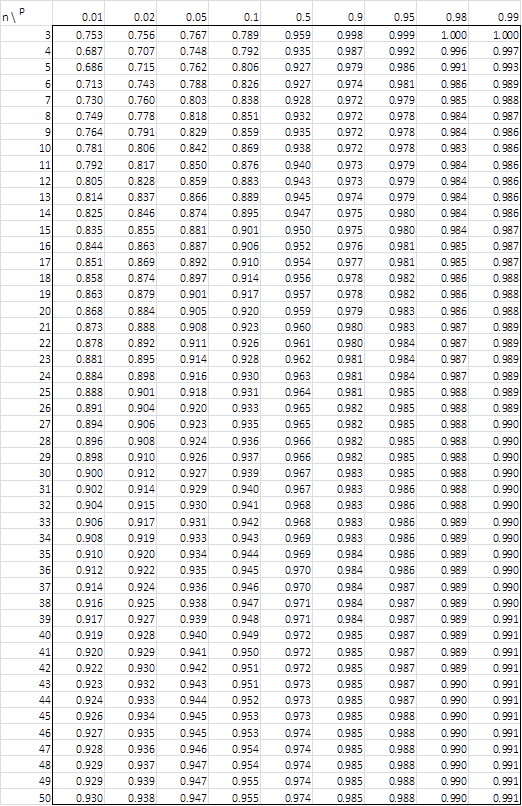
Table 1 contains the weights ai for any given sample size n. Table 2 contains the p-values for Shapiro-Wilk Test. See Shapiro-Wilk Test for more details.

Table 1 – Coefficients

Shapiro-Wilk Weights 1

Shapiro-Wilk Weights 2Shapiro-Wilk Weights 3

Shapiro-Wilk Weights 4

Shapiro-Wilk coefficients n50

Correction: The a13 value for n = 49 should be 0.0919 instead of 0.9190.

Table 2 – p-values

image3742

Download Table

Click here to download the Excel workbook with the above tables.

Reference

Shapiro, S.S. & Wilk, M.B. (1965) An analysis of variance for normality (complete samples). Biometrika, Vol. 52, No. 3/4.

http://webspace.ship.edu/pgmarr/Geo441/Readings/Shapiro%20and%20Wilk%201965%20-%20An%20Analysis%20of%20Variance%20Test%20for%20Normality.pdf

67 thoughts on “Shapiro-Wilk Tables”

  1. Pingback: Statistical hypothesis Testing – coolsoo world

  4. Hello Charles,

    Thanks much for the prompt response. I actually meant the complete Shapiro-Wilk tables.
    On the other hand, after installing the Excel add-in from your website, I prefer using your
    SW Extended Test tool for my application. Great time saver and very informative.
    Is there a way to enlarge the rather small UI on a MacBook Pro 15″ Retina?

    Let me also take the opportunity to thank you personally for creating this wonderful website on statistics with its rich assortment of useful tutorials, examples and tools. Keep up the good work.

    Best regards
    Peter

    Reply

  5. Hi Charles,

    Where can I find the SW tables in a format that allows copying of coefficient columns into my spreadsheet?
    Peter

    Reply

    • Hi Riama,
      There isn’t a Shapiro-Wilk test when n = 2.
      How could you tell whether a sample with only two elements comes from a normally distributed population?
      The value of a normality test with 3 or 4 elements is only marginally useful in my opinion, but two elements?
      Charles

      Reply

      • Good day, Sir,

        I would like to compare the means between two independent groups: A (with N=2) and B (with N=25, normal distribution with Shapiro-Wilk).
        -Should I assume that group A is not normally distributed (because we can’t test the normality) and go with Mann-Whitney test?
        -Or should I assume that group A is normally distributed and go with Independent T test?

        Also, for another case with group X (N=1) and group Y (N=26, normal distribution):
        – can I use the same normal / not normal distribution assumption as the questions above (for N=2)?
        – should I use independent 2-sample statistic test (Independent T-test / Mann Whitney Test) or instead use one sample statistic test vs. a reference mean (one sample T-test / Wilcoxon signed rank test)?

        Thank you very much

        Sincerely yours,
        Lunardi

        Reply

        • Hello Lunardi,
          Where N = 2, I suggest that use both a two-sample t-test and Mann-Whitney to see if the results are similar.
          Where N = 1, I suggest that you use the one-sample t-test using the hypothesis that the mean of the larger sample is the value of the sample with one element. This is appropriate if the larger sample is normally distributed. If not, then use the one-sample Signed-Ranks Test.
          Charles

          Reply

  8. Hello Charles,

    I’m using the table for n=9. I got W=0.718, however the lowest on Table 2 is 0.764 for p value 0.01. Any idea on how to handle this problem?

    Thank you.

    Reply

      • Hello Charles,
        I still don’t quite understand. It’s less than 0.01 so that usually means we reject the hypothesis that it has normal distribution with 99% certainty right? But you said that it’s sufficient. Could you please elaborate on that?

        I tried the enhanced test but the NORMSINV formula can’t seem to work on my excel.

        Thank you so much!

        Reply

        • Hello Dea,
          A p-value < .01 would usually be considered sufficient to reject the assertion that the data comes from a normally distributed population. I don't know why a formula using the NORMSINV function would not work. Perhaps you mean to use the NORMINV function. You could try the NORM.S.INV or NORM.INV function. Charles

          Reply

  9. Hi Charles,

    I have searched for a while trying to find the tables in text form so that I can copy and paste them into excel and perform a vlookup function on them. I cannot find them other than in an image which would mean I would have to manually enter them. Any chance you could provide an excel file with the numbers entered? Thank you!

    Reply

  10. Dear Zaiontz,

    With Shapiro-Wilk Original Test formula in your site, I will do Shapiro-Wilk Test.
    If sample cnt is more than 50, how can I refer the coefficeints and P – value ?
    The table above is only 50 but my sample is more than 2,000.

    And what’s the difference between Shapiro-Wilk Original Test and Shapiro-Wilk Expanded Test ?

    Best Regards,

    Minhwa Lee.

    Reply

    • Hello Minhwa,
      The original test is the version that Shapiro and Wilk developed. It only handles up to 50 data elements. The expanded version was developed to expand the number of data elements up to 5,000. When you have more than 50 data elements I suggest that you use this latter version (it can also be used for 50 or fewer data elements).
      Charles

      Reply

      • Dear Charles,

        Thank you for your prompt reply.
        I have another question.
        I ‘d like to know what data elements exactly mean on example below .
        Which one is data elements ?
        – Sample count = 10 : the number of units in each sample
        – Lot count = 2,000 : the number of lots
        – Sample count * Lot count = 20,000 : All raw data sorted

        I am looking forward to hearing from you.
        Thank you.

        Example
        Lot number raw data value
        (lot couunt=2000) (sample count = 10 )
        ——————————————————————
        Lot 01 2,4,4,3,6,5,3,4,5,3
        Lot 02 3,5,2,3,6,5,3,4,5,3
        Lot 03 3,4,4,7,6,5,3,4,5,3
        …….
        Lot 1999 4,5,2,3,6,5,3,4,5,3
        lot 2000 4,3,4,7,6,5,3,4,5,

        Reply

        • Hello Minhwa,
          If you need to determine whether all the data are normally distributed then you need to test all 20,000 elements. What is considered to be the collection of data elements is not something I can answer; it depends on why you need to check for normally at all. If you need to determine whether all the data are normally distributed then you need to test all 20,000 elements.
          Charles

          Reply

          • Dear Charles,

            Thank you so much your kindly reply.
            I am sorry but I have another question.

            Even though the concerned data elements of mine are more than 50(usually more than 1000), I want to use the original version because it has much less complicated formula than the expanded version.

            If possible by original version, Could you advice me on how to refer to Coefficients and p-value ?
            – how to test the large data by original version.

            Thank you.

  11. Hi Dear Charles,

    I am trying to create coefficient and p value tables in excel, can you please hint the formula that I need to enter?

    Thank you

    Reply

  12. Hi,

    I have a list of 500 numbers that I need to implement my own Shapiro-Wilk test code. That means I need to have 500 coefficients, right? If yes, how can I calculate them? I tried formula on wikipedia, but I could not made it. Thanks in advance for your kind help.

    Reply

  13. Hi Charles,
    thanks for such a post. I am trying to test the normality of Dunn index values (of approx 30 results) obtained from several experiments. Since Dunn index values are fractional, the value of W (in my case it is 0.493, for n=30) is not even close to the values given in table 2. How should I proceed?

    Reply

  16. Hi Charles,
    Thanks a lot for the very helpful explanation.
    However, I’m a bit confused.

    For n=25, I obtain W=0.97, thus p-value of 0.6.
    For alpha=5%, therefore, my hypothesis is not rejected.
    However, the more I diminish the alpha (1%, 0.5%, etc.) the more the hypothesis is “not rejected” as alpha is further away from the p-value. I’m confused, shouldn’t it be harder and harder to have a “non rejection” when I diminish the level of error ?

    Isn’t there a mistake and it should be that the p-value should be below alpha (and not higher than) for a non-rejection ?

    Thanks for your help,
    Thomas

    Reply

  17. Dear Dr. Zaiontz,

    am I right by assuming the Shapiro-Wilk-Tables presented on this page are only applicable for Tests within a Significance Level of 5 %?

    Thank you for providing this knowlege and also for this great webside.

    Best regards
    Max

    Reply

  19. hi,
    i need the values for n=60 and n=100. but i can´t find them nowhere. and p-values,of course. can you help me? unfortunately my knowledge of math isn´t that good.
    thanks.
    anna

    Reply

    • Ann,
      I don’t know of a table with such high values of n. For values of n larger than 50, you could use the Real Statistics SWPROB function (or better yet the SWTEST function) instead of statistics table. See the following webpage
      Shapiro-Wilk Test
      Charles

      Reply

  22. Thanks for the great instructions! However, my results in SPSS and other stats tools yield different p-values (W value is the same) than this example. The first example gives a p-value of 0.873, but SPSS and other tools gives the p-value of 0.922. Is there a reason for this difference?

    Reply

    • The website gives two ways of calculating the p-value for the Shapiro-Wilk test. The original method gives a p-value of .873 based on a linear interpolation, while the Royston method gives a value of .922, which is the same as that provided by SPSS.
      Charles

      Reply

  23. Hello Dr. Zaiontz,

    Thank you, this really helped!

    I would like to ask, what if your W value is lower and out of the table? Example: n=20, computed W=0.8222. I looked at the table and the value at p=0.01 is 0.868

    What should I do to find the p-value?

    Thank you.

    Reply

    • Johanna,
      From the table all that you can conclude is that p < .01. In the next release of the Real Statistics Resource Pack you will be able to use the Royston approximation to compute a more exact value, which in this case will be .001888. I hope to have the next release out this week, hopefully tomorrow if I have time enough to complete all the testing. Charles

      Reply

  24. Hi Charles,
    I just started to study statistics and I am trying to calculate Shapiro-Wilk (W) by myself. For this task I need to find the coefficient table 1 for n= 78 from a1 untill a35. Could you help me? Thank you
    Raphaela

    Reply

  25. Hi Dr. Zaiontz,

    Thank you so much for creating this website! It’s very helpful!

    I wonder how we can generate the p values using the W score and other results from Shapiro-Wilk without looking up this table?

    Best,
    Amelia

    Reply

Leave a Comment