One-Sample Kolmogorov-Smirnov Table

The following table gives the critical values Dn,α as described in Kolmogorov-Smirnov Test.

Kolmogorov-Smirnov Table

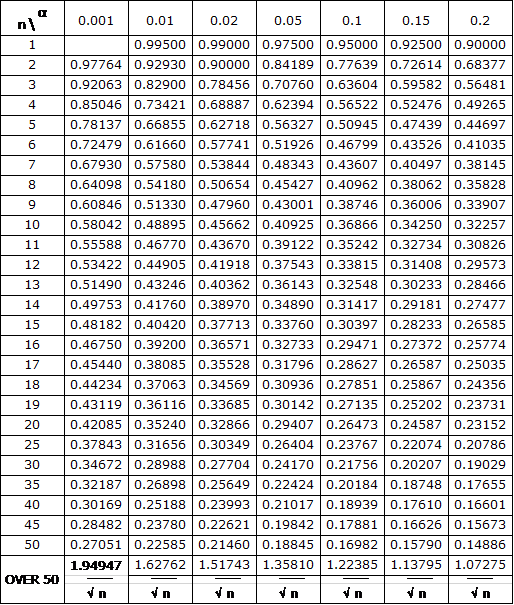
Download Table

Click here to download the Excel workbook with the above table.

References

Kanji, G. K. (2006) 100 Statistical tests. 3rd Ed. SAGE
https://methods.sagepub.com/book/100-statistical-tests

Lee, P. M. (2005) Statistical tables. University of York
https://www.york.ac.uk/depts/maths/tables/

Zar. J. H. (2010) Biostatistical analysis 5th Ed. Pearson
https://www.pearson.com/us/higher-education/program/Zar-Biostatistical-Analysis-5th-Edition/PGM263783.html

83 thoughts on “One-Sample Kolmogorov-Smirnov Table”

    • You find the p-value in the same manner as for unimodal data. Whether the KS test is appropriate depends on what you are trying to use the test for. If you are testing for normality, then either the data is only marginally bimodal or you shouldn’t even bother to test the data since the normal distribution is not bimodal. In any case, I would use a different test for normality (usually Shapiro-Wilk), since the KS test is not the best.
      Charles

      Reply

  3. Hi Charles,
    Thanks for sharing the information.
    I have a doubt.
    The test statistic value of the KS test is known to me. I need to determine the p-value of the KS test. I am trying to apply the KSPROB function, but I couldn’t find the function in excel. Please provide me a solution. I will be really grateful to you.

    Reply

  5. Hi Charles

    As stated in many literature that I read, when parameters are determined from the data, then the critical value is invalid for KS test. Hence, it is required to perform Monte Carlo simulations to find critical values. Since this values are not available in literature, can you suggest a way to find them? I would like to test goodness of fit test for one data for generalized extreme value, generalized logistics and Pearson type 3 distributions.

    Thanks!

    Reply

  7. Hi Charles,

    I am examining whether two sets of samples are drawn from the same population, neither is expected to have a normal distribution.

    I set everything up to do the Two-sample KS test, which worked fine – but then realised that since one sample has a few hundred samples (n) and the other has tens of thousands (m), my Dmn is always going to be a tiny number and the null hypothesis is uniformly rejected.

    Is there a more appropriate non-parametric test I should be using for my situation?

    Thanks,
    J

    Reply

  9. Dear Charles,

    Regarding the K-S test, I am a little bit confused about the interpretation.

    My understanding is that the D parameter (sup(F(x)-F0(x))) should be as small as possible to have the theoretical distribution fitting the sample.

    I also understand that if D<Dn,a, then the theoretical distribution fits the sample.

    However, in that frame, I would expect Dn,a being smaller when a get smaller. Could you please explain ?

    Kind regards,

    Michel.

    Reply

  11. Dear Charles

    Your site is indeed instructional and very helpful in assessing and inferring on data. My request was, can you show how nested logit model can be done in excel.

    Best

    Reply

  12. Dear Charles Zaiontz,
    thank you for this helpful page. My question is: Do you know of an effect size measure (in the sense of Cohen, 1988) for the K-S-test – and ultimately, do you have a hint for calculating the optimal sample size for this test given alpha + beta?
    Thank you very much,
    Robert

    Reply

    • Wiwik,
      You need to interpolate between the two values that are in the table, namely between 40 and 45. You can also use the Real Statistics KSCRIT function which does the interpolation for you. In particular, for alpha = .05
      =KSCRIT(43) yields the value .202955
      Charles

      Reply

  15. Hi, I am trying to calculate the critical D in a two sample KS test but I am facing some difficulties.
    My populations have different sizes: e.g. 60 and 80. I have seen that the formula for D-crit for the 0.05 level is:

    Dm,n,α = KINV(α)*SQRT((m+n)/(m*n))
    So I would assume that in my case D-crit = 1.35810 * SQRT((60+80)/(60*80))?

    Based on the table though the critical value is
    D-crit = 1.35810 / sqrt (n)

    I do not understand whether my KINV(a) is 1.36 or it should be 1.35810/sqrt(n)

    Could you please help me? Sorry if this is too obvious.

    Thank you in advance
    Vasiliki

    Reply

    • Hello Vasiliki,
      Yes, KINV(.05) = 1.3510 (this is a more precise estimate than 1.36). As you have figured out, n = 80*60/140 = 34.28571
      Thus, D-crit = 1.3510/sqrt(34.28571) = .231939.
      You can get the same result by using the Real Statistics formula =KS2CRIT(60,80,0.05,2)
      Charles

      Reply

  17. Good day, l am testing my data for normality using kolmogorov-Smirnov test. Now l have managed to calculate the maximum value and my sample size is 219. Please advice on how l can get the cretical values now? can l generate them using excel or l have to get them from some where, if yes where?

    Reply

  19. Dear Charles,

    Thank you for sharing!

    I have a question: it is not clear to me how critical values are obtained for n over 50? is it alpha/sqrt(n)? I tried this formula and compare it to what obtained from Easyfit but the values are totally different… Do you have any guidance?

    BR

    Reply

  20. Hello Charles,
    I use the K-S test to test differences in the distributions of electrophysiological data, so I often end up having quite a high n. Up to what n value can I consider the K-S analysis reliable? Your table goes up to n=50, but I often have between 120 and 300 values. Is the test still reliable with this sample size?
    Thank you very much in advance!

    Reply

  21. “Charles,
    Yes, I agree – so if the sample K-S statistics is critical D at 0.05, so we must then accept the null hypothesis at the 0.01 level, and then at the 0.01 level, etc.
    Put another way, would we reject the null hypothesis at the 0.05 level but accept it at the 0.01 level if the the sample,K-S statistic lay between these values (ie D.01 > K-S statistic > D.05)? Robert” I’ve a same problem too.

    My alpha 0.2 is more restrict than 0,01. Why?

    Reply

    • The critical region for alpha = .01 is smaller than the critical region for alpha = .05. You could reject the null hypothesis at the .05 level, but retain it at the .01 level.
      Charles

      Reply

  23. I would like to learn if I could use K-S test for normality, for big figures like 1.4 E10, 2.04 E09, 4.6E09 (Estimated bacteria amount in milk etc.) without taking log.

    Reply

    • Alberto,
      You can probably use the KS test for normality, but in general I suggest that you use Shapiro-Wilk test.If you do use the KS test and estimate the mean and standard deviation from the sample, then you should use the Lilliefors table.
      Charles

      Reply

    • Eliza,
      This is covered on the website. I suggest that you type Kolmogorov into the Search bar (under the topic menu on the right side of any webpage) to see how the critical value of the KS test is used.
      Charles

      Reply

  26. How can we “accept” the null hypothesis H0? We fail to reject the alternative,
    not less, not more. The NHST was not constructed to accept whatever H0 or Ha.
    Think that the procedure is completely unfair to Ha, in fact we not reject it
    unless the pvalue is less than 1-alpha, that is 0.05 , 0.01.
    So there are a lot of cases that p>0.05 (say) notwithstanding H0 is untrue.
    “Accepted?”.

    Reply

    • Bibliography
      https://statistics.laerd.com/…/hypothesis-testing-3.ph…
      . . . shows that the significance level is below the cut-off value we have set (e.g., either 0.05 or 0.01), we reject the null hypothesis and accept the alternative hypothesis. Alternatively, if the significance level is above the cut-off value, we fail to reject the null hypothesis and cannot accept the alternative hypothesis. You should note that you cannot accept the null hypothesis, but only find evidence against it.

      Reply

  27. The numbers that you have reported for D_n is in contrast with the values at the wiki page :
    https://en.wikipedia.org/wiki/Kolmogorov%E2%80%93Smirnov_test

    Look at the “Two-sample Kolmogorov–Smirnov test” at the wiki page, for two samples of different sizes n and n’, If one defines n=n’, she will get D_n bigger than what you have reported for n over 50 in this page…with a factor of sqrt(2). which one is correct?

    Reply

    • The Wikipedia page that you reference provides the exact same values as the one sample KS table on my site. In any case, the Wikipedia table is referring to the two sample test whereas as the referenced table on my site is for the one sample test. I describe the two sample KS test on the following webpage
      Two Sample Kolmogorov-Smirnov Test
      Charles

      Reply

  30. Charles,
    In the Kolmogorov-Smirnov table, the critical value of D increases as alpha (1-P) decreases for a given N. This would imply that if a sample K-S statistic is < the critical D value at say the .05 level, then it must also be < the critical D value at the .01 level. This does not seem logical to me – what am I missing?
    Robert

    Reply

    • Robert,
      We reject the null hypothesis that the data comes from a specific distribution when the sample K-S statistic > the critical value (not less than it).
      Charles

      Reply

    • Adrian,
      I have found a few versions of the two-sample KS table, but they are all different, and so I have been reluctant to put one of these on the website. For this reason I provided a distribution function to calculate these values, as described on the webpage
      Two Sample Kolmogorov-Smirnov Test.
      Charles

      Reply

Leave a Comment