Shapiro-Wilk Original Test

Basic Concepts

We present the original approach to performing the Shapiro-Wilk Test. This approach is limited to samples between 3 and 50 elements. By clicking here you can also review a revised approach using the algorithm of J. P. Royston which can handle samples with up to 5,000 (or even more).

The basic approach used in the Shapiro-Wilk (SW) test for normality is as follows:

  • Arrange the data in ascending order so that x1 ≤ … ≤ xn.
  • Calculate SS as follows:

image3595

  • If n is even, let m =  n/2, while if n is odd let m = (n–1)/2
  • Calculate b as follows, taking the ai weights from Table 1 (based on the value of n) in the Shapiro-Wilk Tables. Note that if n is odd, the median data value is not used in the calculation of b.

image3598

  • Calculate the test statistic W = b2 ⁄ SS
  • Find the value in Table 2 of the Shapiro-Wilk Tables (for a given value of n) that is closest to W, interpolating if necessary. This is the p-value for the test.

For example, suppose W = .975 and n = 10. Based on Table 2 of the Shapiro-Wilk Tables the p-value for the test is somewhere between .90 (W = .972) and .95 (W = .978). You can estimate this p-value using interpolation (see Interpolation).

Examples

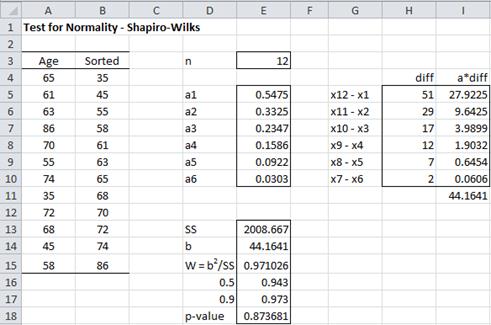
Example 1: A random sample of 12 people is taken from a large population. The ages of the people in the sample are shown in column A of the worksheet in Figure 1. Is this data normally distributed?

Shapiro-Wilk test Excel

Figure 1 – Shapiro-Wilk test for Example 1

We begin by sorting the data in column A using Data > Sort & Filter|Sort (see Sorting and Filtering) or the Real Statistics QSORT function (see Sorting and Removing Duplicates), putting the results in column B. We next look up the coefficient values for n = 12 (the sample size) in Table 1 of the Shapiro-Wilk Tables, putting these values in column E.

Corresponding to each of these 6 coefficients a1,…,a6, we calculate the values x12 – x1, …, x7 – x6, where xi is the ith data element in sorted order. E.g. since x1 = 35 and x12 = 86, we place the difference 86 – 35 = 51 in cell H5 (the same row as the cell containing coefficient a1). Column I contains the product of the coefficients and difference values. E.g. cell I5 contains the formula =E5*H5. The sum of these values is b = 44.1641, which is found in cell I11 (and again in cell E14).

We next calculate SS as DEVSQ(B4:B15) = 2008.667 (cell E13). Thus W = b2 ⁄ SS = 44.1641^2/2008.667 = .971026 (cell E15).

p-value using interpolation

We now look for .971026 when n = 12 in Table 2 of the Shapiro-Wilk Tables and find that the p-value lies between .50 and .90. The W value for .5 is .943 and the W value for .9 is .973.

Interpolating .971026 between these values (using linear interpolation), we arrive at p-value = .873681. Since p-value = .87 > .05 = α, we retain the null hypothesis that the data are normally distributed. Since this p-value is based on linear interpolation, it is not very accurate, but the important thing is that it is much higher than the alpha value, and so we can retain the null hypothesis that the data is normally distributed.

Comparison with other tests

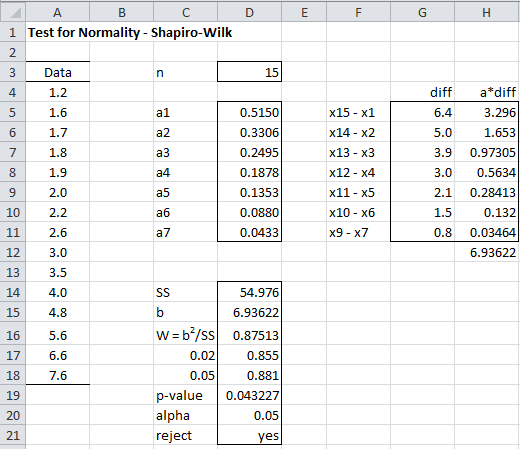
Example 2: Using the SW test, determine whether the data in Example 1 of Graphical Tests for Normality and Symmetry (repeated in column A of Figure 2) are normally distributed.

Shapiro-Wilk example

Figure 2 – Shapiro-Wilk test for Example 2

As we can see from the analysis in Figure 2, p-value = .0432 < .05 = α, and so we reject the null hypothesis and conclude with 95% confidence that the data are not normally distributed, which is quite different from the results using the KS test that we found in Example 2 of Kolmogorov-Smironov Test, but consistent with the QQ plot shown in Figure 5 of that webpage.

Real Statistics Support

Real Statistics Function: The Real Statistics Resource Pack contains the following functions.

SHAPIRO(R1, FALSE) = the Shapiro-Wilk test statistic W for the data in R1

SWTEST(R1, FALSE, interp) = p-value of the Shapiro-Wilk test on the data in R1

SWCoeff(n, j, FALSE) = the jth coefficient for samples of size n

SWCoeff(R1, C1, FALSE) = the coefficient corresponding to cell C1 within sorted range R1

SWPROB(n, W, FALSE, interp) = p-value of the Shapiro-Wilk test for a sample of size n for test statistic W

The functions SHAPIRO and SWTEST ignore all empty and non-numeric cells. The range R1 in SWCoeff(R1, C1, FALSE) should not contain any empty or non-numeric cells.

When performing the table lookup, the default is to use the recommended type of interpolation (interp = TRUE). To use linear interpolation, set interp to FALSE. See Interpolation for details.

For Example 1 of Chi-square Test for Normality, SHAPIRO(A4:A15, FALSE) = .874 and SWTEST(A4:A15, FALSE, FALSE) = SWPROB(15,.874,FALSE,FALSE) = .0419 (referring to the worksheet in Figure 2 of Chi-square Test for Normality).

Note that SHAPIRO(R1, TRUE), SWTEST(R1, TRUE), SWCoeff(n, j, TRUE), SWCoeff(R1, C1, TRUE), and SWPROB(n, W, TRUE) refer to the results using the Royston algorithm, as described in Shapiro-Wilk Expanded Test.

For compatibility with the Royston version of SWCoeff, when j ≤ n/2 then SWCoeff(n, j, FALSE) = the negative of the value of the jth coefficient for samples of size n found in the Shapiro-Wilk Tables. When j = (n+1)/2, SWCoeff(n, j, FALSE) = 0 and when  j > (n+1)/2, SWCoeff(n, j, FALSE) = -SWCoeff(n, n–j+1, FALSE).

Examples Workbook

Click here to download the Excel workbook with the examples described on this webpage.

Reference

Shapiro, S.S. & Wilk, M.B. (1965) An analysis of variance for normality (complete samples). Biometrika, Vol. 52, No. 3/4.

http://webspace.ship.edu/pgmarr/Geo441/Readings/Shapiro%20and%20Wilk%201965%20-%20An%20Analysis%20of%20Variance%20Test%20for%20Normality.pdf

174 thoughts on “Shapiro-Wilk Original Test”

  2. Hello Charles,
    In SWTEST, is it possible to use a named array argument for R1, rather than a cell reference? e.g. =SWTEST(MyDataArray,FALSE,TRUE)
    I haven’t had any success.
    Thank you so much for your excellent work!

    Reply

    • Hello Wade,
      THis should work. I just tried it to confirm that it does work. You need to make sure that MyDataArray references an array with more than 3 cells.
      Charles

      Reply

  3. Sir why you just cant include in the discussion on how to get the p-value by interpolating. It seems there is a missing link for your readers to perform this statistical test.

    Reply

  4. Hi Charles, I had more than 2000 samples of insects. They consist of 37 species, 15 genera. Can I check the distribution normality of this data using Shapiro-Wilk test or other test.?

    Reply

  5. Ciao Carlo! Ho applicato il test di Shapiro-Wilk ad un set di 15 dati, ma la W mi esce maggiore di 1! Ciò trova riscontro nel fatto che b^2 sia maggiore della SS, ma come interpreto ciò? Si considera che il p-value sia sicuramente maggiore di 0,05 (quindi impossibilità a stabilire che la popolazione non abbia una distribuzione normale) oppure devo usare un’altra tipologia di test statistico? Grazie mille

    Reply

  6. Hi,
    Long time reader, first time poster. Thanks for providing this resource!

    Say I’ve got two groups (A and B) of 10 samples each and I want to run a t-test. But first, I want to check for a normal distribution.

    Should I test for normality separately in groups A and B, or subtract out the mean difference between groups A and B (like if B is 0.5 bigger than A, then subtract 0.5 from all the values in B) and then test both A and B together to get a single result? In my mind’s eye, it seems that grouping A and B without addressing the potential for a significant difference might tend to lean SW towards finding a non-normal distribution if A vs B is significant.

    Thanks for reading,
    -Eric

    Reply

    • Hi Eric,
      This depends on which t-test you plan to use. If A and B are independent samples and you plan to run a two-sample t-test, then you should check the normality of each sample (actually the population from which the samples are derived). If instead, you are testing pairs of elements, one from A and one from B, then the paired t-test is appropriate, in which case you would form a new set C consisting of the differences between the pairs and check the normality of C. Which of these tests to use depends on the null hypothesis you are trying to test and the nature of your data.
      In either case, you don’t need to subtract the mean differences. Depending on what you had in mind, this shouldn’t affect the issue of normality anyway.
      Charles

      Reply

      • Hi Charles,

        Thanks for the reply. It’s an unpaired heteroscedastic (Welch’s) t-test on quantifiable mRNA level from independent samples in group A vs group B.

        More info if you’re curious. I have hundreds of these tests to do (the measurement technology- nCounter, measures 100s of separate mRNA species in parallel). Typically, a single normalization strategy is applied to the entire array, and we just take our lumps, so-to-speak, on any rows of data that stay ‘weird’. But some want each row in that normalized array of data to be checked again, and if some mRNA species still have non-normal distributions, to at least report it, if not transform it a second time (probably by ranking) and re-test.

        Thanks again for the reply, I will get to work…
        -Eric

        Reply

  7. Hi Charles,
    Is there a case study when n=3? In biology, when n is equal to 3 is it normally considered a normal distribution? This question has been bothering me. I’d like to hear your opinion.
    Thanks！

    Reply

    • Hi Zhou,
      The test does include the case where n = 3, but I don’t know how much value it has since with so few sample elements, I don’t think you can say much about whether the data comes from a normally distributed population.
      Charles

      Reply

  8. Hi,
    I was wondering what to do if your value isn’t included on the table? My answer was 0.5627 for n=12. This is lower than the lowest value in the table – should I use the lowest value (0.01) as the value or something else?
    Thanks!

    Reply

  9. Hi Charles,

    Thank you for your website ! it is really usefull !

    I have some questions, when I use your formulas to make original test of SW, I have differents result compare to the result I can find on internet simulator (e.g. https://www.statskingdom.com/shapiro-wilk-test-calculator.html) or in R programm. I think simulator doesn’t use the original test of SW, can you confirm ? If I understand well, original test is better for small sample (<50), is it correct ?

    Thanks in advance.

    Reply

    • Hello François,
      I looked at the internet simulator that you referenced, and I observe the following:
      1. For n <= 50 they do seem to use the original SW test based on the critical values for alpha = .01, .02, .05, .1, .5, .9. .95, .98, .99. 2. For alpha values between .01 and .99 they claim to use harmonic interpolation. When I use harmonic interpolation, I get slightly different results. I don't know why this is the case. Note that Real Statistics uses log interpolation. I am not sure which is better, but the results are almost the same. 3. For values of alpha less than .01 or greater than .99, the internet simulator abandons the original SW test and uses the Royston approach. Real Statistics simply returns p-value = .005 for alpha < .01 (i.e. when the W value is lower than the smallest table value) and p-value = .995 for alpha > .99 (i.e. when the W value is larger than the largest table value). I think that the approach used by the internet simulator is better in this case and I will change to this approach in the next release of Real Statistics.
      4. My understanding is that the original version of the SW test is better than the Royston version for n <= 50. Charles

      Reply

  10. Hi, I was wondering if there is a shapiro Wilk Multivariate. I know it supposed to exist but does it also exist in the real statistics Ad-In?

    Reply

  11. What is the formula for p-value?
    My W = 0.9751 and my N = 41. The p-value I got from the software is 0.4968 but I don’t know how to get it manually.

    Reply

  12. Hey there! What’s the syntax for SWTEST? What is the true/false in the second argument? Also what’s h in the third argument? Thanks tons!

    Reply

    • Hello Noah,
      If the second argument is FALSE, then the original Shapiro-Wilk test is used, while if this argument is TRUE, then the Royston version of the test is used. This is explained further on the webpage.
      The h should actually be labeled interp. I have now changed this on the webpage. This argument is used to indicate which type of interpolation is used, again as explained on the webpage.
      Charles

      Reply

  13. Hi Charles,
    Bit of a strange question but here goes, does it make sense to modify a normality test if my data was weighted?
    I’ve seen sources which discuss weighted means, weighted standard deviations and such but am not able to find anything on adapting normality tests which consider weights of the data. Any help is much appreciated!
    Best,
    Matt

    Reply

  16. Hello I am by no means an engineer or someone how manages numbers on a daily basis.
    I installed real statistics on a mac but I can’t find any of this functions on “Data” in Excel.
    I know it’s basic but I am supposed to get the answers via real statistics not step by step on excel.

    Thank you!

    Reply

  17. Hola. Buenas noches.
    Por favor, podría responderme la siguiente pregunta:
    Al utilizar la función en el Excel “=shapiro()” me sale un W de 0.875207. Pero cuando yo realizo el procedimiento de su ejemplo me sale un W de 0.87513.
    ¿Por qué los resultados de W son diferentes?
    Te agradezco tu respuesta.

    Reply

    • Hello Wilzon,
      There are two versions of the test> the original version by Shapiro and Wilk and a subsequent one by Royston. Both are described on the Real Statistics website and both are supported by the Real Statistics software. The Royston version handles much bigger samples since the original version only supported samples up to 50 elements. The results are similar but not exactly the same.
      Charles

      Reply

  18. Ciao Charles,
    ho cercato di seguire passo passo il tuo esempio per sapere se questa è una distribuzione normale o log-normale.
    nella mia serie di dati 6 valori (2,66 4,08 6,78 7,24 12,8 15,8)
    perché il P-Value calcolato con la previsione lineare in excel mi viene 0,487
    W p
    0,826 0,1
    0,927 0,5
    0,924 0,487
    mentre con la formula
    0.05+(0.5-0.1)*(0.924-0.826)/(0.927-0.826) il P-value è 0,437
    la distribuzione è comunque normale con alpha 0.05 giusto?
    grazie per il sito e le informazioni molto chiare

    Reply

    • Ciao Rob,
      If you use the original version of the Shapiro-Wilk test you get p.value = 487, as you have stated. THis result is consistent with the data being normally distributed. I don’t understand the second calculation that you made.
      Charles

      Reply

  20. Thanks for the write up. I have a question, I used the Shapiro Wilk test and my p-value is 0.050. How should I interpret it, normal or non-normal distribution.

    Reply

  21. Hi Charles,
    I have the following table:
    avg sigma
    a 10 5
    b 11 6
    c 15 18
    d 2 3
    e 20 8

    Lets assume a to e are normal distribution each is based on 1000 samples. That’s all what I have. If a and b for instance would contain the same avg and sigma => a is identical to b. I would like to find what is the closest distribution to a, etc. Can I use Shapiro-Wilk for it?

    Reply

    • Abraham,
      Since you said that all of the samples follow a normal distribution and the best estimates of the population mean and standard deviation are the corresponding sample values, the best estimate for a is a normal distribution with mean 10 and standard deviation 5.
      Charles

      Reply

Leave a Comment