Basic Concepts
The saturated model for Example 1 of Three-way Contingency Tables takes the form:
where terms involving C and G require 2 – 1 = 1 coefficient and terms involving T require 3 – 1 = 2 coefficients. Thus terms involving CG, CT, GT and CGT require 1 ∙ 1 = 1, 1 ∙ 2 = 2, 1 ∙ 2 = 2, and 1 ∙ 1 ∙ 2 = 2, respectively. This can be seen from the following expanded form
using a suitable coding of the categorical variables, such as:
tC = 1 if cured and = 0 otherwise
tG = 1 if male and = 0 otherwise
tT1 = 1 if therapy 1 and = 0 otherwise
tT2 = 1 if therapy 2 and = 0 otherwise
In the general case where
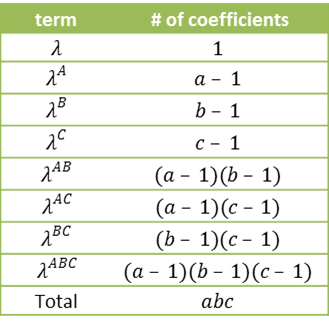
Figure 1 shows how many coefficients are required for each term, assuming A takes on a values, B takes on b values and C takes on c values.
Figure 1 – Number of coefficients
Summary
Thus the saturated model has abc coefficients and no degrees of freedom. Other models will have a number of degrees of freedom which corresponds to the number of coefficients that are missing from the model (based on Figure 1).
As in the two-way case, the expected value of any cell in the contingency table for the saturated model is the same as the observed value of that cell. Thus, expijk = obsijk, or alternatively the probability that an observation will occur in cell ijk is pijk = obsijk / n.
Examples Workbook
Click here to download the Excel workbook with the examples described on this webpage.
Reference
Howell, D. C. (2010) Statistical methods for psychology (7th ed.). Wadsworth, Cengage Learning.
https://labs.la.utexas.edu/gilden/files/2016/05/Statistics-Text.pdf