Basic Concepts
The mean of successive squared differences (MSSD) of the data sequence S = {x1, …, xn} is defined as
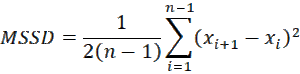
If a data sequence is random then MSSD is approximately equal to the variance. In fact, we can use the following statistic to test the null hypothesis that a data sequence is random
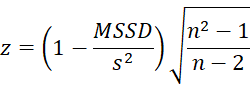If the null hypothesis holds, then for large n this statistic has a standard normal distribution. The normal approximation is pretty good for α = .05 and n ≥ 10, or α = .025, .10, .25 and n ≥ 25, or α = .01, .005 and n ≥ 100.
Example
Example 1: Calculate the MSSD statistic for the data series in column A of Figure 1. Determine whether this data is random.
Figure 1 – MSSD calculation
Cell B4 contains the formula =A5-A4 and cell C4 contains =B4^2, to fill in the other cells, highlight range B4:C17 and press Ctrl-D. The formulas for the other cells are shown in column H. Using the normal distribution approximation, we see that p-value = .036 < .05 = α, demonstrating that the series is not random.
Note that the MSSD value can also be calculated by the Excel formula
=SUMXMY2(A5:A18,A4:A17)/(2*COUNT(A4:A17))
Worksheet Functions
Real Statistics Functions: The Real Statistics Resource Pack provides the following array function where R1 is a column array containing the data series.
MSSD(R1, lab): column array containing the values: MSSD, sample variance, z-statistic, and p-value; if lab = TRUE (default = FALSE), then a column of labels is appended to the output
For Example 1, the formula =MSSD(A4:A18) outputs the value 2.8214, the value shown in cell F5. The array formula =MSSD(A4:A18,TRUE) outputs the range E5:F10 with rows 7 and 8 omitted.
The MSSD function uses the normal distribution approximation to obtain the z-statistic and p-value. Especially for small samples, a better approximation can be obtained for the critical value of the z-statistic (using a table of critical values of the c statistic). From these critical values, we can estimate the p-values. These can be obtained for values of n from 8 to 150 by using the following functions:
MSSD_CRIT(n, α, interp) = critical value for the z-statistic based on a sample of size n and a significance level of α (default .05); when interpolation is required, then the recommended interpolation is used when interp = TRUE (default); otherwise linear interpolation is used.
MSSD_PROB(z, n, iter, interp, txt) = p-value for the z-statistic z based on a sample of size n; interp is as for MSSD_CRIT; iter = # of iterations required to make the approximation (default 40); when txt = FALSE (default), then a p-value less than .005 is rounded down to 0 and a p-value greater than .25 is rounded up to 1, while if txt = TRUE then such values are returned as “< .005” and “> .25” respectively.
For Example 1, MSSD_CRIT(F7) = 1.647945 and MSSD_PROB(F9,F7) = .034446.
Examples Workbook
Click here to download the Excel workbook with the examples described on this webpage.
Reference
Zar. J. H. (2010) Biostatistical analysis 5th Ed. Pearson
von Neumann, J., Kent, R. H., Bellinson, H. R., Hart, B. I. (1947) The mean square successive difference
https://projecteuclid.org/journals/annals-of-mathematical-statistics/volume-12/issue-2/The-Mean-Square-Successive-Difference/10.1214/aoms/1177731746.full