Hypothesis Testing using the Central Limit Theorem

Basic Concepts

Using the Central Limit Theorem we can extend the approach employed in Single Sample Hypothesis Testing for normally distributed populations to those that are not normally distributed. Suppose we take a sample of size n, where n is sufficiently large, and pose a null hypothesis that the population mean is the same as the sample mean; i.e.

If we assume the null hypothesis, we know from the Central Limit Theorem that the sample mean has a normal distribution

This approach works well provided the variance of the population is known, which is not so common.

As we saw in Property 3 of Estimators, the variance of the sample is an unbiased estimator of the variance of the population, and so when the variance of the population is not known, we can estimate σ² by s².

As was done in Confidence Intervals for Sampling Distributions we can now set a confidence interval for the population mean as follows:

Worksheet Functions

Excel Functions: Excel provides the following functions that can be useful in hypothesis testing.

Z.TEST(R1, μ₀, σ) = 1 – NORM.DIST(x̄, μ₀, , TRUE) where x̄ = AVERAGE(R1) = the sample mean of the data in range R1 and n = COUNT(R) = sample size. The third parameter is optional; when it is omitted the value of the sample standard deviation of R1 is used instead; i.e. Z.TEST(R1, μ₀) = Z.TEST(R, μ₀, s) where s = sample standard deviation = STDEV(R1).

CONFIDENCE.NORM(α, σ, n) = k such that (x̄ – k, x̄ + k) is the confidence interval for the mean based on the normal distribution; i.e. CONFIDENCE.NORM(α, σ, n) = z_crit ∙ std err, where n = sample size, σ = population standard deviation (or sample standard deviation s used as an estimate for σ), and 1 – α is the confidence %.

These two functions were not available in versions of Excel prior to Excel 2010. Instead, the equivalent functions ZTEST and CONFIDENCE were available.

Z.TEST and ZTEST ignore any empty cells and cells with non-numeric values.

Observations

Z.TEST(R1, μ₀, σ) represents the probability that the true sample mean is greater than the observed sample mean AVERAGE(R1) under the assumption that the population mean is μ₀. This is a right-tailed test (i.e. it assumes that x̄ ≥ μ₀). If x̄ < μ₀ then Z.TEST will return a value > .5.

If a left-tail test is desired (assuming x̄ ≤ μ₀), then use 1 – Z.TEST(R, μ₀, σ). If a two-tail test is desired then use 2 * MIN(ZTEST(R, μ₀, σ), 1 – Z.TEST(R, μ₀, σ)).

We could have calculated the confidence interval in Example 1 of Confidence Intervals for Sampling Distributions as follows:

CONFIDENCE.NORM(.05, 20, 60) = 5.06, and so the 95% confidence interval is (75 – 5.06, 75 + 5.06) = (69.94, 80.06).

Example

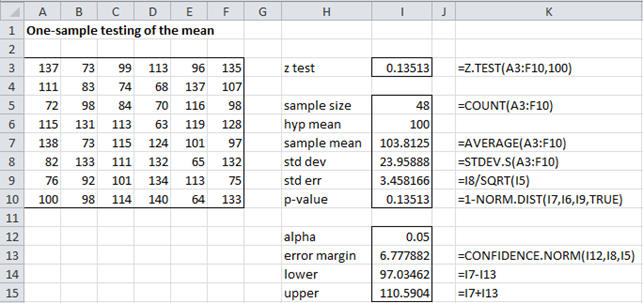
Example 1: A company selling batteries claims that the average life for its batteries before a recharge is necessary is at least 100 hours. One of its clients wanted to verify this claim by testing 48 batteries as described in Figure 1. Is the company’s claim correct?

Figure 1 – One sample testing of the mean

We test the following null hypothesis:

         H₀: μ ≤ 100

Since the sample size is sufficiently large (n = 48 ≥ 30), based on the Central Limit Theorem, the sampling distribution of the mean should be approximately normal with distribution N(x̄, ). Since the population standard deviation is not known we use the sample standard deviation (23.96) as an estimate for σ, and so the standard error is

Since the sample mean x̄ = 103.81, assuming the null hypothesis we can compute the p-value as follows:

p-value = 1 – NORM.DIST(103.81, 100, 3.46, TRUE) = .135 > .05 = α

Since p-value > α, we cannot reject the null hypothesis, and so conclude there is not enough evidence to show that the company’s claim is false. Alternatively, we can arrive at the same result by using the Z.TEST as follows:

p-value = Z.TEST(A3:F10, 100) = .135 > .05 = α

Observation: If we had run a two-tail test, we could calculate CONFIDENCE.NORM(α, s, n) = CONFIDENCE.NORM(.05, 23.96, 48) = 6.78, and so the 95% confidence interval is (103.81 – 6.78, 103.81 + 6.78) = (97.03, 110.59). Since the hypothetical mean of 100 lies in this interval, we must retain the null hypothesis.

More Worksheet Functions

Real Statistics Functions: The Real Statistics Resource Pack contains the following worksheet functions:

STDERR(R1) = STDEV(R1) / SQRT(COUNT(R1)), i.e. standard error for the data in R1

NORM_CONF(R1, α) = CONFIDENCE.NORM(α, STDEV(R1), COUNT(R1))

NORM_LOWER(R1, α) = AVERAGE(R1) – NORM_CONF(R1, α)

NORM_UPPER(R1, α) = AVERAGE(R1) + NORM_CONF(R1, α)

All these functions ignore any empty cells and cells with non-numeric values. If α is omitted it defaults to .05.

For Example 1, we have STDERR(A3:F10) = 3.46, NORM_CONF(A3:F10, .05) = 6.78, NORM_LOWER(A3:F10, .05) = 97.03 and NORM_UPPER(A3:F10, .05) = 110.59.

Examples Workbook

Click here to download the Excel workbook with the examples described on this webpage.

Reference

Howell, D. C. (2010) Statistical methods for psychology, 7th Ed. Wadsworth. Cengage Learning
https://labs.la.utexas.edu/gilden/files/2016/05/Statistics-Text.pdf