Definition
Definition 1: Let x be a random variable with normal distribution N(μ,σ2). Now consider a random sample {x1, x2,…, xn} from this population. The mean of the sample (called the sample mean) is
x̄ can be considered to be a numeric value that represents the mean of the actual sample taken, but it can also be considered to be a random variable representing the mean of any sample of size n from the population.
The standard deviation of the sample mean (viewed as a random variable) is called the standard error of the mean.
Properties
By Property 1 of Estimators, the mean of x̄ is μ (i.e. x̄ is an unbiased estimator of μ) even if the population being sampled is not normal. By Property 2 of Estimators, the variance of x̄ is σ2/n, and so the standard error of the mean is σ/.
When the population is normal, we have the following stronger result.
Property 1: If x is a random variable with N(μ,σ2) distribution and samples of size n are chosen, then the sample mean has the normal distribution N(μ, σ2/n).
Click here for a proof of Property 1.
Observations
As the sample size increases the standard error of the mean decreases, and so the precision of the sample mean as an estimator of the population mean improves.
See Special Charting Capabilities for how to graph the standard error of the mean.
Example
Example 1: Test scores for a standardized test are normally distributed with a mean of 200 and a standard deviation of 40. If a random sample of 16 test papers is taken, what is the expected mean of the sample and what is the expected standard deviation of the sample around the mean (i.e. the standard error of the mean)? What if the sample has size 100?
The mean of the sample is expected to be 200 in either case. The standard error when n = 16 is 40/4 = 10, while the standard error when n = 100 is 40/10 = 4.
Reference
Howell, D. C. (2010) Statistical methods for psychology, 7th Ed. Wadsworth. Cengage Learning
https://labs.la.utexas.edu/gilden/files/2016/05/Statistics-Text.pdf
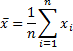
Dear Charles,
I do appreciate your effort for establishing such extremely helpful website, which I am benefiting for more than 2 years. I have a case where sample data has a known margin of error e.g. 5%, which means that the average could be presented as (x̄ +/- 5%). I don not know how this error would affect the confidence interval for μ? Should I calculate the standard error and percentage interval using x̄ and add 5% to the result?
I appreciate your advice.
Best regards,
Samir
Hello Samir,
1. I assume that when you say that the sample data has a margin of error of 5% you mean that a data value of say 7 could be any value between 6.65 and 7.35. If so, one approach would be to generate simulated samples. If say A1:A50 is a range with your original data points, you would create a new sample by placing the formula =$A1*(.95+.1*RAND()) in cell B1, highlighting the range B1:B50 and pressing Ctrl-D. You now calculate the standard error for the data in B1:B50 and place that value in cell B52. You now need to do this a large number of times to create the simulated samples. This can be done 1,000 times, for example, by highlighting the range B1:ALM52) and pressing Ctrl-R. Now if you take the average of the values in range B52:ALM52, you will have an estimate of the standard error.
2. This is similar to the approach used in bootstrapping.
3. Note that the value .95+.1*RAND() above is used to generate a number between .95 and 1.05. You can use other formulas to make the error normally distributed instead of uniformly distributed as done above.
Charles
Dear Charles,
Thank you very much for your highly appreciated advice.
Best regards
How can we use these formulas to in a sample which size is less than 30? Impact 16.
Sampath,
Use the formulas with whatever value of n you have. However it is usually better to use the t distribution instead, especially with small samples. See
One sample t test
Charles
I don’t understand one thing, why does the expected standard deviation of the sample reduce as n increases. So if I consider all 200 test papers, the expected sd of the sample will be 40/sqrt(200) = 2.8. Shouldn’t the expected sd of the sample would be same as that of the population (i.e. 40) as I have included all the observations?
I apologise for the blunder. I thought 200 as the sample size which is not obviously the case.
I don’t have any confusion.
Hi Charles,
Why is it necessary to use the standard error instead of just using STDEV.S?
Since STDEV.S returns the standard deviation of a sample, how is it that the standard error also returns the standard deviation of a sample but gives a different result?
Given the way they’re worded I’d think they’re different versions of the same thing.
Thanks,
Jonathan
Jonathan,
In this case, the standard error is equal to the standard deviation divided by the square root of the sample size. The standard error is what you use based on the Central Limit Theorem.
Charles
Dear Charles,
first of all, thank you very much for your extremely interesting website: I’m learning statistics again !
Regarding this page, I was wondering why the Theorem 1 was a stronger result than those given above, since they were already stating that the mean µ of the sample mean x bar are equal and its variance is sigma / sqrt(n) ? More precisely, if these rules apply generally, then they should also apply to a N(µ,sigma), and hence yield directly to the Theorem 1. Why is it “stronger” ?
Thanks in advance,
Best regards,
Gilles
Giles,
It is stronger because the theorem also asserts that x-bar is normally distributed.
Charles