Basic Concepts
The UCON algorithm for building a Rasch model with dichotomous scores can be extended to more than scores of 0 or 1, i.e. to polytomous scores. These types of models are appropriate for Likert scores and for exams with partial credit.
Notation
Suppose that we have test data with values xsi as defined in Basic Concepts of Rasch Analysis, except that now we will allow scores of 0, 1, 2, …, m where m is any positive integer including values larger than 1. For any ability parameter β and difficulty parameter δ, we define
where![]()
Here, the Rasch-Andrich threshold parameter τh is defined as the difficulty of obtaining scoring category h relative to category h −1. Note that the same threshold parameters are used for any subject s and item i. For any item i, the difficulty δi parameter can be viewed as the average of the δi + τh. Let
Then for m = 2
![]()
![]()
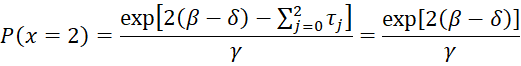
and so
For m = 3, and P(x = 0) and P(x = 1) are as above and
![]()
![]()
![]()
Note too that –τ1 – τ2 can be replaced by +τ3.
Iteration
As in the dichotomous case, the ability, difficulty, and threshold parameters are estimated using an iterative approach. In particular, the threshold value τk,t at step t is calculated by
![]()
![]()
![]()
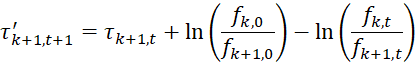
The expected scores xsi,t at step t are calculated as follows:
![]()
The variances at step t > 0 are calculated, as usual, as the sum of squares minus the expected value squared.
![]()
Ability parameter estimation
The ability parameter for subject s at step t is calculated by
where residuals and variance for subject s at step t > 0 are
The standard errors of the ability parameters for t > 0 are
![]()
Difficulty parameter estimation
Similarly, the raw difficulty parameter for item i at step t is calculated by
![]()
where residuals and variance for item i at step t > 0 are
The mean of the raw difficulty parameters is then subtracted from each raw difficulty parameter to obtain the difficulty parameters:
The standard errors of the difficulty parameters for t > 0 are
![]()
References
Wright, B.D. & Masters, G.N. (1982) Rating scale analysis. Chicago: MESA Press
https://research.acer.edu.au/measurement/2/
Ataei, S.and Mahmud, Z. (2015) Rasch-Andrich thresholds in engineering students’ attitudes towards learning mathematics
https://www.semanticscholar.org/paper/Rasch-Andrich-Thresholds-in-Engineering-Students%E2%80%99-Ataei-Mahmud/1b60dc7d5a3be98db220d29b957de55e4550d2e2
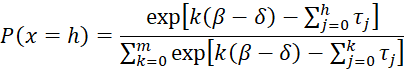
Thanks for taking your time to illsutrate the concepts so well