Example
Example 1: A 10-question multiple-choice test is given to 40 students. Each question has four choices (plus a blank if the student didn’t answer the question). Interpret questions Q1 through Q6 based on the data in Figure 1 where the 20 students with the highest exam scores (High) are compared with the 20 students with the lowest exam scores (Low). The correct answer for each question is highlighted.
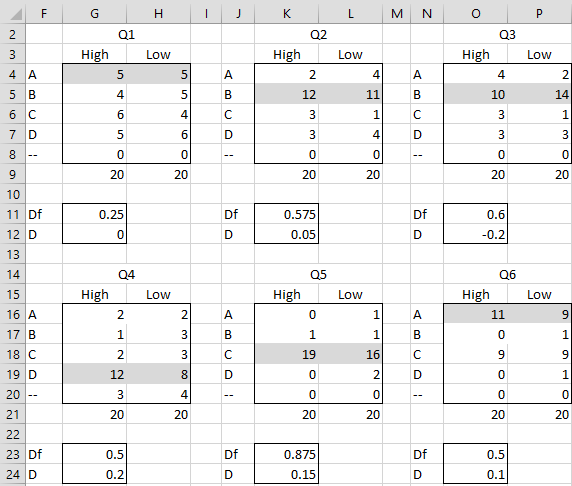
Figure 1 – Item Analysis for multiple choice test
Analysis Q1-Q3
For Q1, Df = (G4+H4)/SUM(G4:H8) = .25 and D = G4/SUM(G4:G8)-H4/SUM(H4:H8) = 0. The four choices were selected by approximately the same number of students. This indicates that the answers were selected at random, probably because the students were guessing. Possible reasons for this are that the question was too difficult or poorly worded.
For Q2, D = 0.05, indicating there is no differentiation for this question between the students who did well on the whole test (top 50%) and those who did more poorly (bottom 50%). The question may be valid, but not reliable, i.e. not consistent with the other questions on the test.
For Q3, D is negative, indicating that the top students are doing worse on this question than the bottom students. One cause for this is that the question is ambiguous, but only the top students are getting tricked. It is also possible that the question, although perfectly valid, is testing something different from the rest of the test. In fact, if many of the questions on the test have a negative index of discrimination, this may indicate that you are actually testing more than one skill. In this case, you should segregate the questions by skill and calculate D for each skill.
Analysis Q4-Q6
Too many students did not even answer Q4. Possible causes are that the question was too difficult or the wording was too confusing. If the question occurs at the end of the test, it might be that the student ran out of time or got too tired to answer the question, or simply didn’t see the question.
Too many students got the correct answer to Q5. This likely means that the question was too easy (Df = .875).
For Q6, approximately half the students chose the incorrect response C and almost no one chose B or D. This indicates that choice C is too appealing and B and D are not appealing enough. In general, one of the incorrect choices shouldn’t garner half the responses and no choice should get less than 5% of responses.
Examples Workbook
Click here to download the Excel workbook with the examples described on this webpage.
References
Zimmaro, D. M. (2016) Writing good multiple choice exams
https://ctl.utexas.edu/sites/default/files/writing-good-multiple-choice-exams-fic-120116.pdf
Vallejo-Elias, J.(2016) Interpretation of discrimination data from multiple-choice test items
No longer available online
McGill University (2025) Guidelines for writing MCQs
https://teachingkb.mcgill.ca/tlk/guidelines-for-writing-mcqs
Quick question, when calculating difficulty, why do we count the blanks? It would seem to me that there are mutiple reasons why a testtaker may not answer a question besides its difficulty. For istance, it might be because they ran out of time or because they simply forgot to answer it. The first reason most likely has something to do with the difficulty of the test as a whole. The other probably has to do with the testtaker. But neither necessarily has anything to do with the item itself. Including the blanks in the calculation can have a large effect when working with small sample sizes. Is there a theoretical or methodological reason for doing so? Thanks!!
Hi Mike,
I agree with your comments. Whether or not you count blanks as wrong, the important thing is to try to understand why so many students left the question blank.
Charles
This approach looks great. I am actually looking for some method to do a bulk item analysis for MCQs on the basis of number of appearances and their respective correct/incorrect attempts. We would not have a single assessment that includes all these questions. Can you suggest some method?
Hello Sachin,
Sorry, but I don’t understand your question.
Charles
Thanks for the reply, Charles! I meant to ask, if I have 20 questions that have been used in multiple assessments. How would I do item analysis in that case?
Hello Sachin,
I don’t completely understand your question. What sort of multiple assessments are you referring to?
Charles
So Charles, let’s say I have an item for which I have data that tells us it was used in 1600 different assessments where there were 800 correct attempts, 350 incorrect attempts and 450 candidates skipped the question. I have this data for ~1000 items. How shall I differentiate among them that which are good, which ones are fair and which question is a poor item.
Hello Sachin,
Let’s assume that each test consists of 10 questions (the items) chosen randomly from a large group of questions. As you have specified, question A was used in 1,600 of these assessments. You can calculate the various metrics (difficulty and discrimination) for question A as described on the website. Even though the specific 10 questions for each assessment will be different (except of course for question A) there will still be a total score, and so you can use this value (for each of the students assessed) when calculating the discrimination value.
As stated above, I have assumed that each student gets a fixed number of questions, and so I don’t understand the significance of a skipped question. Is a skipped question scored the same as an incorrect question?
Charles
Hello, I would like to ask for an interpretation analysis of a 10-item test, for example, if she got 8 correct answers out of 10, what would be her score? Thank you so much.
Jean,
Obviously, she would have a score of 80 out of 100.
Is this what you mean by the “her score”?
Charles
can i ask how to use item analysis using interval data?
like 3- often
2- sometimes
1- seldom
0- never
how can i interpret that using item analysis?
thank you and GOD BLESS
Judy,
If one of these three options is correct, then you can use item analysis as described on the website for multiple choice tests.
Since it is likely that this is not your situation, my question to you is why would you want to use item analysis? What are you trying to find out?
Charles
Charles,
You might want to double check your discrimination index on Q6. It looks like your formula accidentally reverts to using COUNT instead of SUM in the denominator, resulting in an inflated discrimination index.
Daniel,
Yes, you are right. Thank you very much for catching this error. I have now corrected the webpage.
I really appreciate your help in improving the accuracy and usability of the website.
Charles