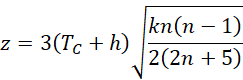Tc correlation between several judges and a criterion

Basic Concepts

T_C is the average of Kendall’s rank-order correlation coefficient between each judge and the criterion ranking.

To calculate T_C, first, create a preference matrix P = [a_ij] as described in Kendall’s u for Paired Rankings. T_C can be calculated via any of the following equivalent formulas

where k = the number of judges, n = the number of criteria, and

A⁺ is the sum of the entries in the preference matrix above the diagonal. It is equal to the number of agreements in ranking the criteria among the judges. Similarly, A^– is the sum of the entries in the preference matrix below the diagonal. It is equal to the number of disagreements in ranking the criteria among the judges.

Hypothesis Test

You can test the null hypothesis that the population parameter corresponding to T_C, i.e. there is no significant agreement among the judges via the z test statistic

which has a standard normal distribution, where

Example

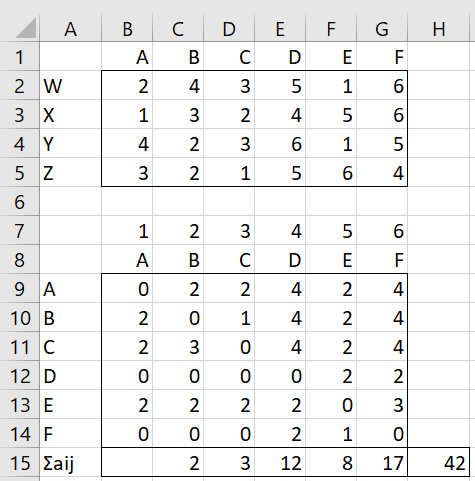
Example 1: Calculate T_C for the data in Figure 1 and determine whether there is significant agreement between the judges.

Figure 1 – Ranking data + preference matrix

The preference matrix and A⁺ = ∑_i<j a_ij is calculated as in Example 1 for Kendall’s u for Paired Rankings. In particular, the preference matrix in range B9:G14 can be calculated by the formula =PREF_MATRIX(B2:G5).

T_C is now calculated and tested as shown in Figure 2.

Figure 2 – T_C analysis

We see from the figure that p-value = .015368 (cell K14), and so we conclude there is significant agreement between the judges (i.e. the population parameter corresponding to T_C is significantly different from zero).

Worksheet Functions

Real Statistics Function: The Real Statistics Resource Pack provides the following function for R1 that contains a preference matrix(w/o headings).

TC_TEST(R1, lab, alpha): returns a column array with T_C-stat, z-stat, and p-value for Kendall’s T_C test on the square preference matrix in R1 (without headings).

If lab = TRUE (default FALSE) then an extra column of labels is appended to the output. alpha is the significance level (default .05).

For Example 1, the formula =TC_TEST(B9:G14,TRUE) produces the output shown in range O9:P11 of Figure 1.

Table Lookup

When k = 2 or 3 and 2 ≤ n ≤ 5, then a table lookup is used instead of the normal approximation described above when the lookup argument is set to TRUE (default). In this case, the z-stat field in the output from the TC_TEST formula takes the value N/A.

In addition, the Real Statistics Resource Pack provides the following worksheet function to generate the p-value for the test in these cases.

TC_PROB(k, n, T_C) = p-value for Kendall’s T_C test when the number of judges is k and the number of criteria being rated is n for the specified value of T_C.

For example, =TC_PROB(3, 5, .4) takes the value .06.

Examples Workbook

Click here to download the Excel workbook with the examples described on this webpage.

Reference

Siegel, S., Castellan, N. J. (1988) Nonparametric statistics for the behavioral sciences, 2nd ed.
https://psycnet.apa.org/record/1988-97307-000