Basic Concepts and Formulas
We next show how to estimate the standard error of Krippendorff’s alpha based on the fact that the ratings would differ if there was a different set of subjects being rated. The formulas we use are as follows:
![]()
![]()
![]()
If the number of subjects in the population of subjects is assumed to be large, then f = 0. If the actual number of subjects is a relatively small finite number, then the calculation of the standard error can be corrected by using the correction factor f = n/N, where N = the number of subjects in the population.
Standard Error Based on Subjects
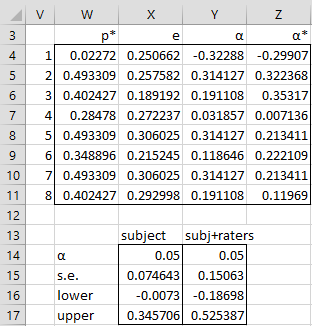
Example 1: Calculate the standard error of Krippendorff’s alpha for Example 1 of Krippendorff’s Alpha Basic Concepts based on subjects.
The calculations are shown in Figure 1.
Figure 1 – Standard Error
Key formulas from Figure 1 are shown in Figure 2.
| Cell | Entity | Formula |
| W4 | p1* | =(U4-$U$17*(T4/$U$15-1)) |
| X4 | e1 | =SUMPRODUCT(I4:L4,$O$22:$R$22)/$U$15-$U$18*(T4/$U$15-1) |
| Y4 | α1 | =(W4-$U$18)/(1-$U$18) |
| Z4 | α1* | =Y4-2*(1-$U$19)*(X4-$U$18)/(1-$U$18) |
| X15 | s.e. | =SQRT(SUMSQ(Z4:Z11-U19)/(U13*(U13-1))) |
| X16 | lower | =U19-X15*TINV(X14,U13-1) |
| X17 | upper | =MIN(U19+X15*TINV(X14,U13-1),1) |
| Y15 | s.e. | =SQRT(X15^2+M5^2) |
| Y16 | lower | =U19-Y15*TINV(X14,U13-1) |
| Y17 | upper | =MIN(U19+Y15*TINV(X14,U13-1),1) |
Figure 2 – Key formulas
The calculation of the ei values depends on the πk* values as shown in range O22:R22 of Figure 3 of Krippendorff’s Alpha Basic Concepts. These values are calculated using the array formula =MMULT(O20:R20,O15:R18). Also, note that the formula for the standard error in cell X15 is an array formula and so you must press Ctrl-Shft-Enter.
From the standard error of .0867, we can calculate the 95% confidence interval (-.0364, 0.375) as shown in cells X16 and X17. Here, we use the formula
kalpha ± s.e. * crit
where crit is the critical value of the t distribution with n – 1 degrees of freedom.
We can also calculate the standard error for raters instead of subjects. We do this using jackknifing. This is done by calculating m values of Krippendorff’s alpha for the data in the rating table, first removing one of the m columns from the table. The variance is then the population variance of these alpha values multiplied by m – 1. The standard error is the square root of this value.
Standard Error Based on Raters
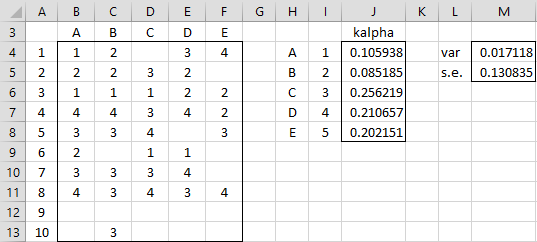
Example 2: Calculate the standard error of Krippendorff’s alpha for Example 1 based on raters.
We do this using the Real Statistics KTRANS and KALPHA functions as shown in Figure 3.
Figure 3 – Standard error for raters
Here cell J4 contains Krippendorff’s alpha for the data in the rating table (repeated in range A3:F13) with the first column (corresponding to rater A) removed. This is calculated by placing the worksheet formula =KALPHA(KTRANS($B$4:$F$13,I4)) in cell J4. The other alpha values are calculated by highlighting the range J4:J8 and pressing Ctrl-D.
The variance (cell M4) is calculated via the formula
=(COUNTA(B3:F3)-1)*VAR.P(J4:J8)
and the standard error of .130835 (cell M5) is calculated by the formula =SQRT(M4).
Total Standard Error
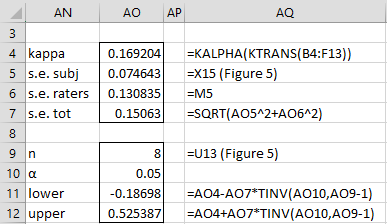
The total standard error, including both subjects and raters, can now be determined, based on the assumption that raters and subjects are independent, since in this case, the total variance is the sum of the two variances. The calculations are shown in Figure 4. We also calculate the 95% confidence interval for Krippendorff’s alpha.
Figure 4 – Total standard error
Examples Workbook
Click here to download the Excel workbook with the examples described on this webpage.
References
Gwet, K. L. (2015) On Krippendorff’s alpha coefficient
https://agreestat.com/papers/onkrippendorffalpha_rev10052015.pdf
Krippendorff, K. (2004) Reliability in content analysis: some common misconceptions and recommendations. University of Pennsylvania paper.
http://faculty.washington.edu/jwilker/559/Krippendorf.pdf
Girard, J. M. (2016) Krippendorff’s alpha coefficient, GitHub
https://github.com/jmgirard/mReliability/wiki/Krippendorff’s-alpha-coefficient
Gwet, K. L. (2015) Standard error of Krippendorff’s alpha coefficient
http://inter-rater-reliability.blogspot.it/2015/08/standard-error-of-krippendorffs-alpha.html
Hello, I have been working my way through your guide for calculating krippendorff’s alpha. However I am unsure what formula to put in cells Y15, Y16 and Y17. Could you advise please? Many thanks, Hannah
Hello Hannah,
I just updated the webpage to include the formulas that you have requested.
Charles
Hi Charles,
Thank you so much for updating this so quickly. For the formula you have added for cell Y15 (s.e. for subject + raters), you have said that it is =SQRT(X15^2+X22^2). In this formula, which figure are you referring to for X22, as I can’t see it within any of the example images? Also is this formula also an array formula, as in X15?
Many thanks,
Hannah
Hi Charles,
Have you had the chance to consider my above query?
Many thanks,
Hannah
Hi Hannah,
Sorry, but I am trying to catch up on some older comments. I will respond shortly.
Charles
Hi Hannah,
Sorry that I made this more confusing than it should be. X22 is not displayed and instead, this should refer to cell M5 in Figure 4.
The total standard error is explained in Figure 4 (cell AO7) and in the explanation of Example 2.
The formula in cell Y15 is not an array formula.
As you may know, all the examples on the website can be found in one of the examples workbooks, which can be downloaded from
https://www.real-statistics.com/free-download/real-statistics-examples-workbook/
The examples described on this webpage can be found in the Correlation-Reliability workbook. The field is called X22 on this examples workbook, although it is equivalent to cell M5. Cell X22 is not shown on the webpage, while cell M5 is shown.
Charles
Hi Charles,
Thank you so much for your assistance. I hadn’t realised that there were examples workbooks, but they look extremely helpful so I will take a look.
Best wishes,
Hannah