Real Statistics Support for Krippendorff’s Alpha

Worksheet Functions

In addition to the KALPHA and KTRANS functions described in Krippendorff’s Alpha Basic Concepts, we now describe some other functions.

Real Statistics Functions: The Real Statistics Resource Pack contains the following array functions:

KRIP_SES(R1, lab, weights, ratings, alpha, scorrection): returns a 4 × 1 column array with the following elements: Krippendorff’s alpha for the data in the Agreement Table in range R1, the corresponding standard error for subjects and the lower and upper ends of the 1 – alpha confidence interval for Krippendorff’s alpha.

KRIP(R1, lab, weights, ratings, alpha, scorrection, rcorrection): returns a 7 × 1 column array with the following elements: Krippendorff’s alpha for the data in the Rating Table in range R1, the corresponding standard error for subjects and the lower and upper ends of the 1 – alpha confidence interval for Krippendorff’s alpha, followed by the total standard error, including subjects and raters) and the lower and upper ends of the 1 – alpha confidence interval corresponding to this standard error.

The weights and ratings arguments are as for KALPHA. alpha is the significance level (default .05). The subject and rater correction factors are the f parameters described in Krippendorff’s Alpha Standard Error.

If lab = TRUE, then an extra column with labels is appended to the output (default is FALSE).

In addition, the Real Statistics Resource Pack contains the following non-array function:

KRIP_SER(R1, lab, weights, ratings, alpha, rcorrection) = the standard error for raters, where range R1 contains data from a Rating Table.

Data Analysis Tool

Real Statistics Data Analysis Tool: We can use Real Statistics’ Interrater Reliability data analysis tool to calculate Krippendorff’s Alpha and its confidence intervals.

For Example 1 of Krippendorff’s Alpha with Non-Categorical Ratings, press Ctrl-m and select the Interrater Reliability option from the Corr tab of the Multipage interface as shown in Figure 2 of Real Statistics Support for Cronbach’s Alpha. If using the original interface, then select the Reliability option from the main menu and then the Interrater Reliability option from the dialog box that appears as shown in Figure 3 of Real Statistics Support for Cronbach’s Alpha.

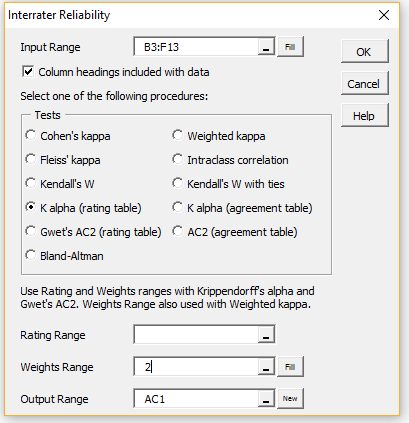
In either case, fill in the dialog that appears as shown in Figure 1 and click on the OK button.

Figure 1 – Interrater Reliability dialog box

Note that 2 in the Weights Range represents interval weights. You would get the same result by entering the range O15:R18 (see Figure 1 of Krippendorff’s Alpha with Non-Categorical Ratings). Upon pressing the OK button, the output shown in Figure 2 is displayed.

Figure 2 – Krippendorff’s Alpha data analysis

Observations

Since the Subject and Rater Factors are set to zero, it is assumed that we have very large populations of subjects and raters. If instead, one or both of these factors is small, then you can change cell AD4 or AD5 to some value between 0 and 1 (the f value described in Krippendorff’s Alpha Standard Error). The values in range AD7:AD13 will automatically be updated.

Note that range AC7:AD13 contains the array formula

=KRIP(B4:F13,TRUE,2,,AD3,AD4,AD5).

If you had entered the agreement table (range I3:L11 from Figure 1 of Krippendorff’s Alpha Basic Concepts) in the Input Range and chosen K-alpha (agreement table), the output would look similar, although no values for the total standard error and confidence interval would be displayed. The output would use the array formula

=KRIP_SES(I4:L11,TRUE,2,,AG3,AG4)

If you had used the ratings in range B16:E16 of Figure 1, you would need to enter B16:E16 (or A17:A20) in the Rating Range in Figure 2.

Examples Workbook

Click here to download the Excel workbook with the examples described on this webpage.

References

Gwet, K. L. (2015) On Krippendorff’s alpha coefficient
https://agreestat.com/papers/onkrippendorffalpha_rev10052015.pdf

Krippendorff, K. (2004) Reliability in content analysis: some common misconceptions and recommendations. University of Pennsylvania paper.
http://faculty.washington.edu/jwilker/559/Krippendorf.pdf

Girard, J. M. (2016) Krippendorff’s alpha coefficient, GitHub
https://github.com/jmgirard/mReliability/wiki/Krippendorff’s-alpha-coefficient

Gwet, K. L. (2015) Standard error of Krippendorff’s alpha coefficient
http://inter-rater-reliability.blogspot.it/2015/08/standard-error-of-krippendorffs-alpha.html