Non-Categorical Ratings for Krippendorff’s Alpha

Example using interval scale

Example 1: Repeat Example 1 of Krippendorff’s Alpha Basic Concepts where the rating categories use an interval scale.

All the formulas remain the same, but we need to change the weights matrix to reflect an interval scale as described in Figure 2 of Krippendorff’s Alpha Basic Concepts. The revised analysis is shown in Figure 1.

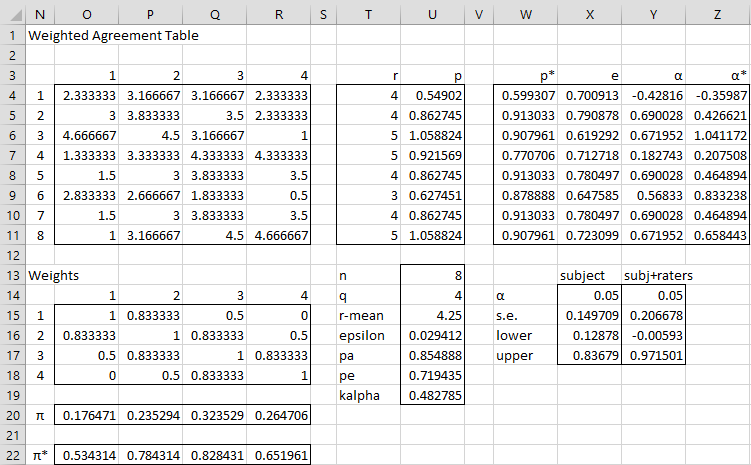
Krippendorff's Alpha interval ratings

Figure 1 – Krippendorff’s alpha with interval scale ratings

Here the weights are calculated by placing the formula =1-(O$14-$N15)^2/($U$14-1)^2 in cell O15, highlighting the range O15:R18 and pressing Ctrl-R and Ctrl-D. Note that this time the weighted agreement table is not the same as the agreement table and the πk* values are not the same as the πk values. Krippendorff’s alpha is much larger than the version using categorical ratings (as calculated in Krippendorff’s Alpha Basic Concepts).

Changes using other scales

If we had used ratings on an ordinal scale (e.g. Likert values), then we would place the following formula in cell O15:

=IF(O$14=$N15,1,1-COMBIN(ABS(O$14-$N15)+1,2)/COMBIN($U$14,2))

If we had used ratings on a ratio scale, then we would use the following formula in cell O15:

=1-((O$14-$N15)/(O$14+$N15))^2

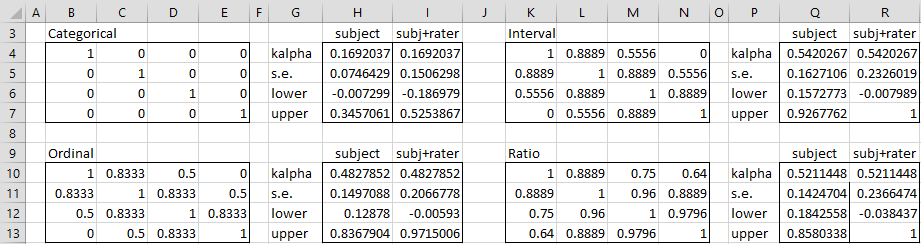
A summary of Krippendorff’s alpha using the four different weights is shown in Figure 2.

Krippendorff's Alpha rating scales

Figure 2 – Krippendorff’s Alpha by Rating Scale

Changes using other ratings

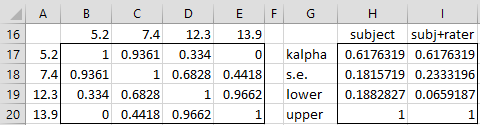
If we had used ratings on an interval scale, but instead of using ratings 1, 2, 3, 4 we had instead used 5.2, 7.4, 12.3, 13.9, then the result would be as shown in Figure 3.

Krippendorff's alpha interval scale

Figure 3 – Interval Ratings

The calculations are the same as for Example 1, except that this time the ratings 5.2, 7.4, 12.3, 13.9 are used. The same result for Krippendorff’s alpha can be obtained by using any of the following formulas (referencing Figure 3 and Figure 1 of Krippendorff’s Alpha Basic Concepts):

=KALPHA(I4:L11,2,C17:F17) or =KALPHA(I4:L11,C18:F21)

=KALPHA(KTRANS(B4:F13),2,C17:F17) or =KALPHA(KTRANS(B4:F13),C18:F21)

Examples Workbook

Click here to download the Excel workbook with the examples described on this webpage.

References

Gwet, K. L. (2015) On Krippendorff’s alpha coefficient
https://agreestat.com/papers/onkrippendorffalpha_rev10052015.pdf

Krippendorff, K. (2004) Reliability in content analysis: some common misconceptions and recommendations. University of Pennsylvania paper.
http://faculty.washington.edu/jwilker/559/Krippendorf.pdf

Girard, J. M. (2016) Krippendorff’s alpha coefficient, GitHub
https://github.com/jmgirard/mReliability/wiki/Krippendorff’s-alpha-coefficient

13 thoughts on “Non-Categorical Ratings for Krippendorff’s Alpha”

  1. Dear Charles,
    thank you very much for setting up this webpages and gathering all these information.

    I am developing an observation protocol and now I want to calculate the IRR for two independent raters. I am using a likert scale with 6 rating options. There are rating categories where the raters used (answered) only 2 of the different rating options (f.e. 1 and 2). If now I am calculating IRR, do I need to ‘tell’ SPSS or Excel that the scale consits out of 6 rating opportunities?
    Because in my calculations the IRR is very low if only two rating options were used by the raters, even they rated only 5 times differently (n=39) –> (Alpha = 0,225).
    In other categories the raters used the whole range of the rating scale (1,2,3,4,5,6); but the answer differt 15 times between the raters. Still using SPSS calculating Krippendorf Alpha; Alpha = 0,7..
    Do you have any idea explaning these different results?
    I am really looking forward to ur answer and ideas.
    Greetings,
    Theres

    Reply

    • Hello Theres,
      If I understand correctly, you are performing a number of IRR, one for each category. Likert ratings of 1,2,3,4,5,6 are used but for some categories both raters only used ratings 1 or 2. Did I understand correctly?
      I don’t know how SPSS supports Krippendorf Alpha, and so I don’t know whether (or how) you need to inform it of the rating scale.
      I don’t know why you got alpha of 0,225 for one category and 0,70 for another. I would need to see the data for this.
      Charles

      Reply

  2. Thank you for this very informative presentation. One area I get stuck on this, is how then would one go about calculating a necessary sample size say for a minimum alpha of .7 or a confidence interval (e.g. .6 – .80) for the alpha? I have scoured and found guidance in using Fleiss’s formula but the difference in the data requirements ratio vs nominal and number of raters though they both account for the same number of raters.

    Reply

  4. Hi Charles,

    A question around the use of the weighted Pi* values.

    I see in your Categorical example that you calculate Pe using the standard Pi values, and assume that there is no difference given that the weightings =1. However, if we use say an ordinal weighting, where do we need consider Pi* (e.g. do we use it in the calculation of Pe)?

    It is not obvious from the above examples whether Pi* has been taken into consideration. I have tested out computing the Pe using the weighted Pi* values, however, it appears to result in KAlpha over >1.

    Thank you very much for any advice on this.

    Reply

  5. Hello Charles,

    Thank you for putting together this resource! I had a quick question for you. I am trying to determine the test/retest reliability for a grading system of MRIs of a specific injury type. 19 reviewers graded 16 MRIs twice, two weeks apart, on a 0-4 scale. Each reviewer graded each image both times. I am trying to determine the inter and intra-rater reliability for this grading system. Do you that a Krippendorff’s alpha with ordinal ratings would be the appropriate way to measure for inter-rater reliability for the system?

    Additionally, to test for the test/retest reliability of this system, I was thinking of using a intraclass correlation (1,1) to look at each grader’s individual retest reliability, and then averaging this correlation across all graders. Do you think that this would be appropriate?

    Thank you for your help!

    Reply

  6. Thank you so much for this!

    Could I ask if the ordinal weights (weights =1) used for Gwet’s AC2 uses the same formula as Krippendorff’s Alpha here?

    =IF(O$14=$N15,1,1-COMBIN(ABS(O$14-$N15)+1,2)/COMBIN($U$14,2))

    Is there a way to cross-check the weights matrix for Gwet’s AC2, or to put custom weights?

    Thank you very much.

    Reply

Leave a Comment