Basic Concepts
In Intraclass Correlation we reviewed the most common form of the intraclass correlation coefficient (ICC). We now review other approaches to ICC as described in the classic paper on the subject (Shrout and Fleiss). In that paper the following three classes are described:
Class 1: For each of the n subjects a set of k raters is chosen at random from a population of raters and each of these raters rate that subject. Note that each subject is potentially rated by different raters.
Class 2: k raters are chosen at random from a population of raters and these k raters rate all n subjects.
Class 3: Each of the n subjects are rated by the same k raters and the results address only these k raters.
The ICC values for these classes are respectively called ICC(1, 1), ICC(2, 1) and ICC(3, 1). Each of these measures the reliability of a single rater. We can also consider the reliability of the mean rating. The intraclass correlations for these are designated ICC(1, k), ICC(2, k) and ICC(3, k).
Worksheet Functions
Real Statistics Function: The Real Statistics Resource Pack contains the following array function:
ICC(R1, class, type, lab, alpha): outputs a column range consisting of the intraclass correlation coefficient ICC(class, type) of R1 where R1 is formatted as in the data range of Figure 1 of Intraclass Correlation, plus the lower and upper bound of the 1 – alpha confidence interval of ICC. If lab = TRUE then an extra column of labels is added to the output (default FALSE). class takes the values 1, 2 or 3 (default 2) and type takes the values 1 (default) or k where k = the number of raters. The default for alpha is .05.
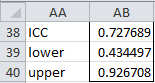
For example, the output from the formula =ICC(B5:E12,2,1,TRUE,05) for Figure 1 of Intraclass Correlation is shown in Figure 1 below.
Figure 1 – Output from ICC function
Data Analysis Tool
Real Statistics Data Analysis Tool: The Interrater Reliability data analysis tool supplied in the Real Statistics Resource Pack can also be used to calculate the ICC.
To calculate the ICC for Example 1 press Ctrl-m and choose the Interrater Reliability option from the Corr tab of the Multipage interface as shown in Figure 2 of Real Statistics Support for Cronbach’s Alpha.
If using the original interface, then select the Reliability option from the main menu and then the Interrater Reliability option from the dialog box that appears as shown in Figure 3 of Real Statistics Support for Cronbach’s Alpha.
In either case, fill in the dialog box that appears (see Figure 7 of Cohen’s Kappa) by inserting B5:E12 in the Input Range and choosing the Intraclass Correlation option. After clicking on the OK button, the output shown in Figure 2 is displayed.
Figure 2 – Output from ICC data analysis tool
You can change any of the values in range AG5:AG7, and the values in range AG9:AG11 will change automatically.
We next show how to calculate the various versions of ICC.
Class 1 Model
For class 1, we use the model
where μ is the population mean of the ratings for all the subjects, μ + βj is the population mean for the jth subject and εij is the residual, where we assume that the βj are normally distributed with mean 0 and that the εij are independently and normally distributed with mean 0 (and the same variance). This is a one-way ANOVA model with random effects.
As we saw in One-way ANOVA Basic Concepts
The subjects are the groups/treatments in the ANOVA model. In this case, the intraclass correlation, called ICC(1,1), is
The unbiased estimate for var(β) is (MSB – MSW)/k and the unbiased estimate for var(ε) is MSW. A consistent (although biased) estimate for ICC is
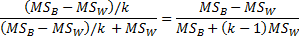Example
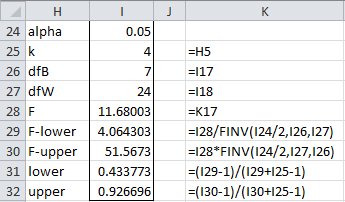
For Example 1 of Intraclass Correlation, we can calculate the ICC as shown in Figure 3.
Figure 3 – Calculation of ICC(1, 1)
First, we use Excel’s Anova: Single Factor data analysis tool, selecting the data in Figure 1 of Intraclass Correlation and grouping the data by Rows (instead of the default Columns). Alternatively, we can first transpose the data in Figure 1 of Intraclass Correlation (so that the wines become the columns and the judges become the rows) and use the Real Statistics Single Factor Anova data analysis tool.
The value of ICC(1, 1) is shown in cell I22 of Figure 1, using the formula shown in the figure.
We can calculate the confidence interval using the following formulas:
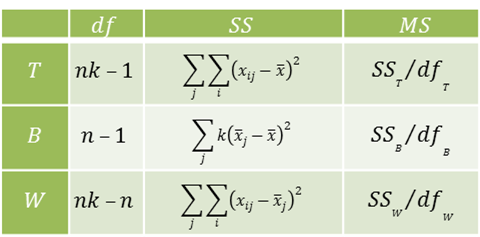
For Example 1 of Intraclass Correlation, the 95% confidence interval of ICC(1, 1) is (.434, .927) as described in Figure 4.
Figure 4 – 95% confidence interval for ICC(1,1)
ICC(1, 1) measures the reliability of a single rater. We can also consider the reliability of the mean rating. The intraclass correlation in this case is designated ICC(1, k) and is calculated by the formulas
ICC(1, 4) for Example 1 of Intraclass Correlation is therefore .914 with a 95% confidence interval of (.754, .981).
Power and Sample Size
The statistical power of the ICC(1,1) test is
where
Here ρ0 is the ICC value when the null hypothesis is assumed to be true and ρ1 is the ICC value when an alternative hypothesis is assumed to be true, where ρ1 > ρ0.
Another Example
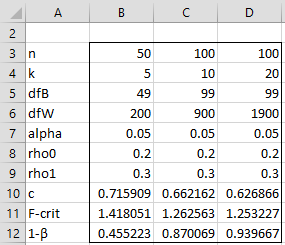
Example 1: Calculate the power when n = 50, k = 5, α = .05, ρ0 = .2 and ρ1 = .3.
We see that the power is 45.5% as shown in column B of Figure 1. The figure also shows the change in power when the sample size increases to 100 and the number of raters increases to 10 and 20.
Figure 5 shows the results of the analysis.
Figure 5 – Statistical power for ICC(1,1)
Real Statistics Support
Real Statistics Functions: The following function is provided in the Real Statistics Resource Pack:
ICC_POWER(ρ0, ρ1, n, k, α) = power of the ICC(1,1) test when ρ0 = ICC based on the null hypothesis, ρ1 = expected value of the ICC (alternative hypothesis), n = the sample size, k = # of raters and α = the significance level (default .05).
ICC_SIZE(ρ0, ρ1, k, pow, α) = minimum sample size required to achieve power of pow (default = .80) where the other arguments are as for ICC_POWER.
For Example 1, ICC_POWER(.2, .3, 50, 5, .05) = .455. The sample size required to achieve 95% power for the same values of is given by ICC_SIZE(.2, .3, 5, .95) = 244.
Real Statistics Data Analysis Tool: The Statistical Power and Sample Size data analysis tool can also be used to calculate the power or sample size requires for the ICC(1,1). See Cronbach’s Alpha Continued for more details.
Class 2 Model
This is the model that is described in Intraclass Correlation. For Example 1 of Intraclass Correlation, we determined that ICC(2, 1) = .728 with a 95% confidence interval of (.434, .927). These are the results for a single rater. The corresponding formulas for the mean rating are as follows:
ICC(2, 4) for Example 1 of Intraclass Correlation is therefore .914 with a 95% confidence interval of (.755, .981).
Class 3 Model
The class 3 model is similar to the class 2 model, except that var(α) is not used. The intraclass correlation, called ICC(3, 1), is given by the formula
Using the terminology of Two Factor ANOVA without Replication (as for case 2), we see that (MSRow–MSE)/k is an estimate for var(β) and MSE is an estimate for var(ε). A consistent (although biased) estimate for ICC is
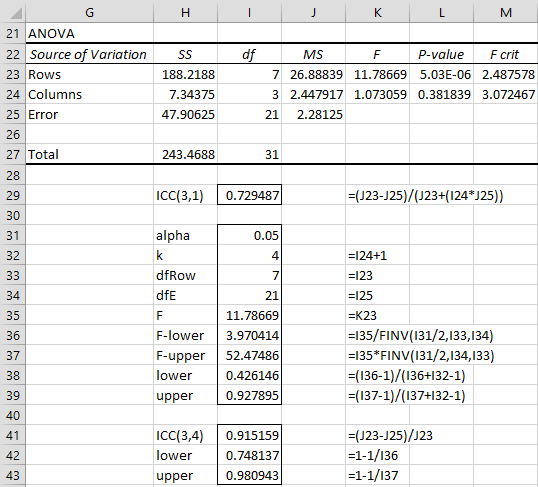
For Example 1 of Intraclass Correlation, we can calculate ICC(3, 1) and its 95% confidence interval as shown in Figure 6 (referring to the worksheet in Figure 2 of Intraclass Correlation).
Figure 6 – Calculation of ICC(3,1) and 95% confidence interval
ICC(3, 4) for Example 1 is therefore .915 with a 95% confidence interval of (.748, .981).
Observation: Class 3 is not so commonly used since by definition it doesn’t allow generalization to other raters.
Observation: ICC(3, k) = Cronbach’s alpha. For Example 1 of Intraclass Correlation, we see that =CRONALPHA(B5:E12) has value .915, just as we saw above for ICC(3, 4).
Examples Workbook
Click here to download the Excel workbook with the examples described on this webpage.
References
Shrout, P .E. and Fleiss, J. L. (1979) Intraclass correlations: Uses in assessing rater reliability. Psychol. Bull., 86: 420-428.
https://www.aliquote.org/cours/2012_biomed/biblio/Shrout1979.pdf
Loo, T. K., Li, M. Y. (2016) A guideline of selecting and reporting intraclass correlation coefficients for reliability research. Journal of Chiropractic Medicine 15, 155–163
https://www.ncbi.nlm.nih.gov/pmc/articles/PMC4913118/
Wu, S., Crespi, C. N., Wong, W. K. (2012) Comparison of methods for estimating the intraclass correlation coefficient for binary responses in cancer prevention cluster randomized trials
https://pubmed.ncbi.nlm.nih.gov/22627076/
Li, L.., Zeng, L., Lin, Z., Cavell, M, Lui, H. (2015) Tutorial on use of intraclass correlation coefficients for assessing intertest reliability and its application in functional near-infrared spectroscopy–based brain imaging. Journal of Biomedical Optics.
https://www.spiedigitallibrary.org/journals/journal-of-biomedical-optics/volume-20/issue-05/050801/Tutorial-on-use-of-intraclass-correlation-coefficients-for-assessing-intertest/10.1117/1.JBO.20.5.050801.full?SSO=1
Hi, I’ve been tasked with calculating ICCs but have some questions you might be able to help with.
I have a subset of about 50 subjects and each subject is given a score by a “Primary” rater and a “Reliability” rater. We have 8 total raters, but 1 or 2 raters of those 8 are more often the “Primary” rater and the rest are more often the “Reliability” raters. This is because those specific 1 or 2 raters have more experience and training than the others. The reason we have a subset of 50 subjects with both Primary and Reliability scores is to run interrater-reliability and make sure all of our raters are giving similar scores for the same subjects.
The score the raters are giving the subjects is a ratio of time the subject spent doing a specific behavior, so the score variable ranges from 0-1.
What type of ICC Class would this be? We’re only interested in making sure that our specific 8 raters are all reliable amongst each other and that the scores they’re getting are reliable.
Hi Katherine,
You say that “We’re only interested in making sure that (a) our specific 8 raters are all reliable amongst each other and that (b) the scores they’re getting are reliable.”
Regarding (a), I understand that when measuring reliability you treat the primary rates the same as the reliability raters. Is this what you want?
Regarding (b), I am not sure what you are trying to measure. Is (b) really the same as (a) or are you seeking some level of consistency of the reliability raters with the “gold standard” of the primary raters?
Charles
Hi
If the number of repetitions (k) is different, how can we calculate ICC and 95%CI?
Thanks
Hi,
Are you saying that the number of raters varies by subject? If so, I suggest that you use a different measurement. E.g. Gwet’s AC2. See
Gwet’s AC2
Charles
Hello Charles,
I have a problem with some of my variables when conducting the ICC. Even though the output indicates a perfect ICC, there a no values for the lower and upper bound in the SPSS output. Do you know why this might be the case?
Hello Luisa,
Sorry, but I don’t use SPSS. Real Statistics provides ICC capabilities in Excel.
Charles
Hi! I would like to calculate inter-rater agreement on scale scores (0=N/a 1=No 2=partial 3=yes) of three rates on 14 questions assessing the quality of 80 research papers. Which is the best model to use according to your opinion and experience?
I have tried ICC but getting some weird negative results when there is almost complete agreement in some questions.
1. Is 2=partial between No and Yes?
2. How should I interpret N/A?
3. Are there 3 raters? Are you trying to get a measure of agreement between these 3 raters?
Charles
Hello Charles
Im trying to get the ICC2,4 equation to work
But I cant seem to get 0.914, nd my CI are 0.755 and 0.981 which are also off
any thoughts
thanks
Chris
Hello Chris,
The example at the beginning of this webpage is for ICC(2,1) and not for ICC(2,4). If you are looking for ICC(2,1) and are not getting the results shown on the webpage, you can send me an Excel file with your data and results, and I will try to figure out what is going wrong. Charles
Hello Charles
ICC class 2 model
I sorted out the formula for ICC2,4 to 0.914 using MSE, MSrow an MScol
now its only the lower and upper that are incorrect
This is the model that is described in Intraclass Correlation. For Example 1 of Intraclass Correlation, we determined that ICC(2, 1) = .728 with a 95% confidence interval of (.408, .950).
These are dependent on the ICC lower / upper of the 2,1 model
From my version of Example 1, I had the lower at 0.434 and the app 0.927
these are different from the values above?
Thanks again for all your help
Im also working the Kripp Alpha I’ll have some questions for that soon
Chris,
Can you email me an Excel file with your calculations so that I can try to figure out why the lower and upper are incorrect?
Charles
sent email to the gmail address
thanks
Hello Chris,
Thanks for sending me your data and calculations and sorry for not understanding what you were telling me in your comment. The values you calculated on your spreadsheet are correct. I get the same values when I use the Real Statistics ICC function. I don’t know why the values shown on the webpage are incorrect. In any case, thank you very much for finding this error. I have now corrected the webpage.
I really appreciate your help in improving the accuracy of the Real Statistics website.
Charles
MY PLEASURE
I hope my spreadsheet wasn’t too confusing
I take your equations and then enlarge it to meet my needs
Dear Charles,
I’d like to apply ICC(3, 2) to my data of 100 ratings from two raters.
1) Am I correct with the assumption that a good to excellent reliability towards an average of the raters’ scores can be concluded if the 95% confidence interval is greater than 0.75?
I got the following scores with alpha 0,05: ICC 0.97, lower .95, upper .98. This would mean that I can form a reliable average, doesn’t it?
2) Also, I’d have to first ensure my data fulfills the assumptions for ANOVA, don’t I?
– Levene’s test is significant
– Normal distribution w/ Shapiro-Wilk test not significant for rater 1, but significant for rater 2 and significant for the average of both raters
-> What are my options here? Can I still interpret the values obtained for the ICC? If so, how and with what limitations?
Thank you!
1. .75 as the lower limit of the confidence interval would usually be viewed as an indication of high reliability, and certainly .95.
2. Yes, the assumptions are not met, but since the calculated ICC value is so high, it is likely that the reliability is high too. You could use another measure of interrater reliability (e.g. Krippendorff’s alpha or Gwet’s AC2). I don’t believe these measures require normality although the confidence intervals are probably based on normality. The Real Statistics website covers these tests.
Also, the following paper may be useful.
https://www.researchgate.net/publication/268370725_Assumptions_behind_Intercoder_Reliability_Indices
Charles
Dear Charles,
May I ask you a question regarding the practical difference between Class 1 and Class 3?
I am from the language testing field. We have a group of raters nad several exam sessions during a year. For one session, each student´s performance is rated by two raters. For individual sessions, there is no overlap in the design, that means that for instance Rater 1 rates always with Rater 2, Rater 3 always with Rater 4, etc. That means two way mixed effect (Class 3). But during the year, when we calculate it for all sessions together and for all raters, the design becomes more complicated, because the pairs of raters are different, randomly assigned (?), for some performances Rater 1 and Rater 3 might form a pair, Rater 2 and Rater 7 might form a pair… That means that the Class 3 design becomes Class 1 (one way random effect), right?
Martina,
Help me understand the scenario better. For every exam, do you have exactly two raters (even though the specific raters will vary)? What sort of rating do the raters give (e.g. values from 0 to 100)? For each session is there one subject or multiple subjects that take the same exam?
Charles
Dear Charles,
Thanks for your reply. An example:
In the exam=session in May, 100 students participated and 6 raters were available. Rater 1 and 2 rated students 1-30, rater 3 and 4 rated students 31 – 70 and Rater 5 and 6 rated students 71 – 100. In this analysis, we analyse only the agreement on the total score – a single number. In this case, am I right when I suppose two-way mixed-effects model applies?
We have several sessions like this, with different students and different combination of pair of raters, but during one year, the sessions are analysed separately.
But after one year (with e.g. 8 sessions like this), we put everything together an we analyse it again. In this case, there are overlaps. Let´s suppose we have 800 students and 15 raters in total, each rater rated with several other raters in pair. For instance, rater 1 rated students 1 – 3 with rater 2, and also students 101 – 130 with rater 5, etc.
In this analysis, it is one-way random-effects model, isn´t it?
Martina,
Thanks for the clarification, but what sort of values are used for the ratings? E.g. students 1-30 were rated by rater 1 and rater 2. What sort of ratings do they give? Numbers like 0 through 10 (like in Olympic diving competitions)?
Charles
In the analysis, we use only final score, like in the Olympic Games, so a value between 0 and e.g. 25.
Thank you.
Hello Martina,
I am not sure any of the classes apply since it doesn’t seem that the raters are chosen at random (class 1 and 2) yet the same raters don’t rate all subjects. I don’t know which approach applies the best. You might be able to use Gwet’s AC2 instead and side-step this issue. See
Gwet’s AC2
Perhaps someone else from the Real Statistics community can offer better insight.
Charles
Dear Charles,
I have some questions about the ICC.
The first one is about the conditions of their use. Because an ANOVA is realized, before using the ICC, should we first check the ANOVA hypothesis (normality of residuals…)? Or can we use them on all data ?
I have repeated data (an observer realize the observation on day 1 and on day 2). I would like to know if the results are stable between days. Can I use ICC3 on these data ?
I also have another type of repeated data. For a particular measure, two observers realized an observation on the morning and afternoon of day 1 and 2 on the same animals. If I want to test 1) the inter-observers reliability, can I use all the data or should I analyze them separately (moorning day 1, afternoon day 1…) 2) test-retest reliability, can I use for one observer data of morning and afternoon or should I also split the data and do the analyze in two parts ?
I hope I’m clear about what I said.
Thank you.
Hello Marianne,
1. To calculate ICC no assumptions are required, but to use the confidence intervals or hypothesis testing you need to satisfy the ANOVA assumptions.
2. I don’t believe that ICC3 can be used without some modification. In any case, I have not yet added this subject to the Real Statistics website. The following articles may be helpful to you:
https://www.uvm.edu/~statdhtx/StatPages/icc/icc.html
https://journals.plos.org/plosone/article?id=10.1371/journal.pone.0219854
https://bmcmedresmethodol.biomedcentral.com/articles/10.1186/s12874-018-0550-6
Charles
Hi Charles,
I have a question about ICC in my study.
There are 344 scans to analyze for one observer, do you think how many scans that need to analyze by another observer to test the ICC?
Hi Yuxin,
Are you asking whether the other observers need to rate the same 344 scans? The answer is yes.
Charles
I’m trying to evaluate inter- (between 2-3 observers) and intraobserver (me doing two measurements 14 days apart) reliability between two different methods of measuring the same object. In this specific case, measuring the same time intervals in the heart using two different ultrasound techniques. In all cases, I’m comparing the average of 3 measurements for each method.
I’ve been reading the article by Koo & Li (2016, https://www.ncbi.nlm.nih.gov/pmc/articles/PMC4913118/), and it seems the ‘Two-way mixed effects, absolute agreement, multiple raters/measurements’ ICC model/type is what best suits my case. However, I’m unsure if this is possible using the Real Statistics Data Analysis Tool, as it seems there doesn’t exist a Shrout and Fleiss (1979) version of this ICC?
Thanks in advance.
Hello Erik,
I have downloaded the article that you referenced and will look into whether I should add this capability to Real Statistics.
Charles
Charles – love this site, it’s such a huge help in my work! Question for you though–is there a way to select a particular ICC form when using the excel add-in? I’m trying to look at interrater consistency (not absolute agreement) across proposal ratings of multiple raters across multiple vendors and multiple dimensions. It would be the ICC (3,k) model. I’ve been using the Corr tab and clicking Intraclass correlation. Separate row for each dimension-vendor combination, and a column for each rater. It is returning ICC type 1 every time.
Hello Jen,
You can change the ICC class on the output. For example, referring to Figure 2, you can change any of the values in range AG5:AG7, and the values in range AG9:AG11 will change automatically. In particular, you can change the value of the class (which is mislabelled as Case) from 1 to 2. I have now updated the webpage to reflect this.
Charles
Hi Charles,
thanks for your explanations! They are very helpful! For my research I have some questions.
1. case: I have measured 32 Patients with a medical System for spine analysis. each of them 5 times. Now I want to determine the reproducibility of the system. Is it better to calculate the Cronbach’s alpha or the ICC for Intrarater-relibility. I think the ICC because it ist not a questionary case? So I would use ICC(3,1) with k=5 and and the 95% Confidence interval? Is there a need to calculate the Signifikanz like a p-valvue? how would I do that?
2. case: I have measured the same patients with a second system for spine analysis. each of them again 5 times. Can I handle those two systems like two raters, and calculate ICC(3,1) with k=2 to determine Interrater-relibility (using the mean of the 5 measurement from system 1 and 2)? Or is it better to use the Bland-Altman method to compare the systems?
hope you understand my questions, Thanks in advance!
Julia
Hi Julia,
1. Yes, Cronbach’s alpha doesn’t appear to be the appropriate tool.
When you say that each patient is measured 5 times, does this mean that the same person/procedure/tool is doing the measurement each time or are there 5 different raters? ICC is based on 5 different raters.
Why are you choosing ICC(3,1) rather than ICC(2,1)?
The Shrout and Fleiss research paper didn’t show how to calculate a p-value, but instead shows how to calculate the confidence interval (which explained on this webpage). This is more useful than the p-value in any case.
2. Probably Bland-Altman is more appropriate. With this tool you are comparing the accuracy of a new method with an existing method.
Charles
Hello Charles,
Thank you so much for you reply, I just saw it.
Yes, each Patient was measured 5 times, but NOT by 5 different rates. It was each time the same tool operated by the same person!
So I am not sure how case 2 and 3 differs when there are no different rates but repeated measurements with the same “rater”.
So ICC(2,k) would be more appropriate because repeated measurements a more like “k raters are chosen at random from a population of raters”?
Thanks again!
Julia
And is it then ICC(2,1) or ICC(2,k),
ICC(2,1) is based on a single measurement, lest say there are 3 rates and each of them made one measurement
ICC(2,k) is based on a single measurement, lest say there are 3 rates and each of them made 3 measurements and for the ICC-calcultaion there ist the mean of those 3 measurements used, is that correct?
But since I have 5 repeated-measurements with the same rater I would choose the ICC(2,1), right?
See my previous comment.
Charles
Hello Julia,
Since each rater rates the subject multiple times, I don’t think any of the ICC measurements is appropriate. This sounds more like Bland-Altman. I found the following paper on the Internet which may be relevant but I have not read the paper and so I am not sure whether or not it addresses your situation.
https://academic.oup.com/ptj/article-abstract/74/8/777/2729337
Charles
Hi Julia, Hi Charles,
Thank you for your explanations!
I am having almost the same issue than Julia. I have been taking measurements on patients with a medical tool. Each patient was tested 4 times with the same tool operated by the same person.
I would like to assess the reliability of the measurements, and until now I was thinking using the ICC 2,1 or ICC 3,1.
But I guess I should have a look on your article if it worked for Julia.
My only issue is that I am measuring XY curves and not single measurements.
So I am wondering what score I should use (std to the mean of the 4 tests for instance) in order to assess the reliability of my measurements ?
Hope you will understand my question,
thank you very much
Antoine
Hi Antoine,
Sorry for the late response.
When you say that “Each patient was tested 4 times with the same tool operated by the same person.”, are there multiple people doing the testing (each 4 times) or is there only one person doing the measuring? Does anything change when making the 4 measurements? E.g. they are maade one hour apart.
When you use the word reliability, what do you mean?
Charles
Hello
Firstly, great package and finally can run ICC in Excel on multiple sets simultaneously.
Having played around with this, I think (although very likely wrong) a slight mistake in the presentation of the underlying theory.
ICC(2,1) and ICC(3,1) are mathematically the same. However, the difference is in how you infer from them. Secondly, the difference between a case 2 and 3 within your package is actually addressing the issue of absolute agreement (which you have labelled as case 2) vs consistency (which you have labelled as case 3).
So, I think your ICC case 2 is actually a case 2/3 with absolute agreement and your ICC case 3 is actually a case 2/3 with consistency.
Hope this helps.
Stuart
Stuart,
ICC(2,1) are not mathematically the same. In fact, if you look at the example given on the webpage, the values for ICC(2,1) are different.
The version of ICC(2,1) that I use is as described in the original paper by Shrout, P .E. and Fleis, J. L. (1979) Intraclass correlations: Uses in assessing rater reliability.
Charles
Thank you Charles – extremely useful tool and webpages! I am still a little confused about which class of ICC to use in my study though. I have hundreds of responses to a survey with dozens of 5-point Likert questions, and want to see if different subgroups of respondents differ significantly in their responses – e.g. Europeans vs. North Americans. After reading these pages, I therefore calculated the average rating of each item for each subgroup, to essentially convert them into two ‘raters’ I could compare, and then used your tool to calculate the ICC(2,2). However, I am not sure if this is really a Class 2 situation, or if it is reasonable to consider each large subgroups as a rater (in this case, k=2). Can you please clarify?
Mike,
I don’t really have enough knowledge about what you are trying to achieve to clarify things further.
Charles
Hi – thanks for this page, it is extremely useful!
A couple questions:
1. I’m trying to run a class 2 “agreement” ICC in excel, and I can’t seem to figure out the correct formula because I can’t tell which number designates which type in the excel formula.
I am inputting: =ICC(data range, 2, __, .05)
I’m not sure what number to put in the __ because I can’t find documentation saying whether 1 is agreement or consistency. I also get different values for higher numbers in that place (1-5 all return different values, but I have no clue what a 3,4, or 5 might be representing). I hope this makes sense, thanks for the help!
2. What is the purpose of the alpha value in the formula? I’ve tried several different values between 0 and 1, and it doesn’t seem to affect the returned value.
Thanks so much!
To clarify: I know what alpha means in the statistical sense, just not its purpose in this Excel formula.
Adam,
1. The Real Statistics function takes the form ICC(R1, class, type, lab, alpha). Here class takes the values 1,2 or 3 (default 2).
type takes the value 1 (default) or k where k = the number of raters.
2. ICC is an array function which returns multiple values. The first of these values (i.e. the only value you see if you only use the Enter key) is not affected by the alpha value. If you treat ICC as an array function, then you will see other values, some influenced by the alpha value. See the following webpage for information about how to use an array function in Excel:
Array Formulas and Functions
Charles
Thank you so much for the rapid response! I looked into how to use an array formula, and I’m still doing something wrong. If I highlight an area of the spreadsheet as a possible location for those multiple values you mentioned, add my ICC formula, then hit Ctrl+Shift+Enter, the range I’ve highlighted fills up with the value I already have, not a table of values (I assume these “multiple values” are things like the confidence interval etc?)
Thanks again!
Adam
Adam,
That is strange. Make sure that the shape of the highlighted range is correct. The range should have two columns if you set lab = True (not two rows).
If you send me an Excel file with your data and analysis I will try to figure out why you aren’t seeing all the output information (including confidence intervals).
Charles
Does this ICC use an absolute agreement or consistency definition?
Thanks!
Charles,
Please look at the following webpage: https://www.ncbi.nlm.nih.gov/pmc/articles/PMC3670985/
Charles
Hello Charles,
I have a problem of testing ICC values by splitting the data in groups. Two raters are measuring each individual. The sample can be divided based on severity. Say I have ICC1 for group 1 and ICC2 for group 2. I can find CI no problem, which are exact. But I need to compare the ICC1 and ICC2 to determine measurements in one group are better agreeable than those of the other group. I attempted a large sample theory but it did not work and it fails badly for small samples. I am looking at n=128 vs. n=9 in one of the comparisons.
Is there a variance formula for ICC in a non-cluster randomized study?
Thanks for your reply in advance!
ps. I tried Fisher’s transformation via atanh in R, which reproduced the exact CI very well. But ICC is not the same as rho (correlation).
Sorry, but I don’t know how to address this. Perhaps someone else in the community can help.
Charles
Dr. Zaiontz:
Thank you very much for your site. In employment testing it is common to conduct oral interviews using three raters/evaluators. With large applicant pools, it may be necessary to assemble multiple panels, and applicants are randomly assigned to only one of the panels. Theoretically, the three interviewers assigned to a panel are randomly assigned from a population of potential interviewers (I say “theoretically” because it’s not easy finding volunteers to sit on these panels!)
It is common for personnel analysts to use Chronbach’s Alpha as a proxy for ICC Class 3 to estimate the mean reliability for a single three-rater panel. Am I correct that ICC Class 2 is a more appropriate estimate? It would seem to be nearly identical to your original example of the wine tasting (which also sounds like a lot more fun than interviews). Thanks.
Hi Charles,
Thank you for this post.
In Figure 5 under the Class 3 Model, the formula for the ICC is displayed in cell K29, referring to another cell H12. However I do not see where the formula (or value) in cell H12 is defined. Can you please clarify what H12 refers to?
Thanks
Paul,
Sorry about that. H12-1 has the same value as the contains of cell I24. In fact, I need to fix the formula to use I24 instead of H12-1.
Charles
Hello Charles,
Thanks for the detail explanation. I am not sure which ICC class I should use to analyse the following:
I have 15 MR Images from 15 subjects. I recruited 4 observers to define the organ contours e.g. Lt and Rt eyes from the images. I recorded the volume of what they had drawn and wanted to assess the inter-observer variability. I ran the repeated measure one way ANOVA and calculated the ICC using the formula on the page “Intraclass Correlation”. The ICC is extremely low while the raw data (volume measured) seems to be similar among different observers. Am I doing it the wrong way? Is it correct to consider ICC class 2? And should I consider the ICC with 4 observers, i.e. ICC(2,4) instead of ICC(2,1) which gave me a very low ICC that seems not making sense?
Many thanks!
Winky
Winky,
1. Which version of the ICC. ICC(1,.), ICC(2,.) or ICC(3,.) depends on what you are trying to measure, as described on the referenced webpage.
2. Whether you use ICC(k,1) or ICC(k,4) depends on whether you want to measure the reliability of an individual (the first version) or the average for the group (the second version). Here k = 1, 2 or 3.
3. Regarding whether you are doing the calculations correctly, if you send me an Excel file with your data and calculations, I will try to see whether the calculations are correct. You can send it to the email address on the Contact Us webpage.
Charles
Charles
Hi Charles,
Thanks for the great article, it has been highly useful. I had a question regarding 95% CI interpretation in regards to ICCs.
I executed an ICC on data from 3 judges and came up with the following results:
ICC 0.752241391
95% Lower CI -0.497986439
95% Upper CI 0.946442785
Obviously that is a fairly high ICC and degree of agreement/reliability. However, I am not sure how to interpret the 95% CIs. I have always been taught that a CI containing 0 or 1 means the test statistic is not significant. Is that the case here as well?
I have seen previous comments eluding to this same question but could not gleam a definitive answer from them on this topic.
Thank you for your help,
Shelby
Shelby,
Since zero is in the 95% CI, the test statistic (namely the ICC value) is not significantly different from 0. Thus even though the calculated ICC value looks pretty high, statistically speaking the population value of the ICC may be zero.
The fact that your 95% CI is so wide is probably due to the fact that you have very few subjects being evaluated.
Charles
Hi Charles,
In that case can we use the ICC or is it not valid
Aznila
Aznila,
What are you referring to when you say “in that case”?
Charles
Hi Charles.
I have been trying to figure out whether I should use an ICC or Fleiss Kappa analysis. I have multiple raters, who rated 17 groups on 8 different categories. The ratings range low to high. Every rater doesn’t rate all groups, but all groups are rated multiple times on each category. I am not sure how to set up the data or which I should use. I haven’t gotten a handle on how to use the software you’ve provided. Can you provide any additional guidance?
Lyn,
Fleiss’s Kappa is used when the ratings are categorical. ICC is used when the ratings are numerical, even ordinal data which can be viewed as numeric.
Fleiss’s Kappa does not require that every rater rate every subject, but that all subjects get the same number of ratings. ICC does require that every rater rate every subject.
It might be that your situation is a partial fit for ICC and a partial fit for Fleiss’s kappa. That may be a problem and so you may need to find a different measurement.
Charles
Dear Dr. Charles,
firts, let me congratulate again with you for your site and for the help you provide us!
I would like to put to your attention this paper that describes an interesting case of Class 2 Inter-Rater and Intra-Rater Reliability assessment, in which there are k raters, each one rating all n subjects of the population, by performing m measurements on every subject.
The peculiarity of this approach is that the m measurements by the i-th rater on the j-th subject are not averaged together but are considered individually, so allowing more detail in model variances estimation.
This is the link:
http://ptjournal.apta.org/content/ptjournal/74/8/777.full.pdf
I’m not one of the authors so I’m not doing self-promotion, I just hope you and all the community can find it useful!
Regards
Piero
Thanks Piero for sharing this with us.
Charles
Hello Charles,
I may be wrong, but should the lower CI level for the mean used in the class 2 model example (0.914) be 0.860 as opposed to 0.734?
Thanks for your time.
Just realised I was wrong. Please ignore my comment.
Apologies and thank you for your time.
First, thanks for this post on ICC calculations using Excel. In the first “Intraclass Correlation” I believe you calculated ICC(2,4) = 0.728, whereas in the “Intraclass Correlation Continued” you refer to this as ICC(2,1) = 0.728, whereas for k=1, the calculation for ICC reverts to a simpler formula (with no dependence on k) which yields a value of 0.914.
As I understand it the ICC(2,4) applies when one is interested in the reliability of the average group score for the wine, whereas the ICC(2,1) examines the judge to judge reliability. Might it be inferred that ICC(2,1) relates to the reliability of the wine score, but that ICC(2,4) focuses on the reliability of the judges?
Robert,
In the first “Intraclass Correlation” I calculated ICC(2,1) = 0.728, although I was not so clear about the terminology since ICC(2,1) is the usual intraclass correlation.
Also ICC(2,4) = 0.914.
I am not sure about what you intend by “reliability of the wine score” and “reliability of the judges”. The ICC is measuring the reliability/agreement of the judges in evaluating wine scores.
Charles
Thanks for your reply. I think my confusion is because the formula for ICC(2,1) is a function of k, whereas ICC(2,k) is not a function of k! I’ve read elsewhere that the inference is that ICC(2,1) estimates the reliability of a single observer rating the wines (even though you use k=4 to obtain this estimate; ICC(2,4) is the reliability estimate using the mean of the 4 judges to assess the wine quality (but is not a function of k=4).
Robert,
That is an interesting observation. Of course, k is indirectly used in the calculation of ICC(2,1) when calculating MSRow and MSE.
Charles
Hi Charles;
I got the result of ICC = 0.649, CI 95% (lower bound (-2.366) and upper bound (0.964)).
How can I report this result please?
Many thanks.
Here is the reporting for different data:
A high degree of reliability was found between XXX measurements. The average measure ICC was .827 with a 95% confidence interval from .783 to .865 (F(162,972)= 5.775, p<.001). I believe that the lower bound for the ICC is -1/(n-1). Thus your CI lower bound of -2.366 seems quite surprising. Charles
Many thanks for your reply.
Can I assume the lower bound zero. and reported as 0.65 (o to 0.96)??
Regards
Thank you Charles.
Something went wrong with the message I sent and made it impossible to understand.
Here follows my message again:
1. What does me not feel at ease with ICC is that after having calculated the ICC value and the 95% confidence interval, I find no way of interpreting rationally the results, which is of course essential for myself and for the jury who is concearned. I read your answer to Sravanti of July 24, 2015: there is no agreement as to what is an acceptable value for ICC, although you have typically seen .7 used. So what to do if ICC<.7 ?
2. I read about Cohen's interpretation of effect size of an experimental manipulation:
phi square = theta square/sigma square.
For phi square = .01 the effect is called "small". For phi square = .0625 the effect is called "medium big". For phi square = .16 the effect is called "big"
A from phi square derived parameter is eta square = phi square/(phi square + 1) with a range [0;1]. It looks like a correlation coëfficiënt, and its estimator gives an impression of the relative size of the factors and combination of factors in Variance Analysis. So, an effect is "small" for eta square =.010, is "medium big" for eta square =.059, and"big" for eta square = .138.
Wouldn't there be a way of transposing to ICC ? Thank you once more.
Erik
Erik,
Sorry, but I don’t know a way of transposing these to ICC. Please note that even the effect size guidelines (small, medium, large) by Cohen and others are really rough and not appropriate for all circumstances.
Charles
Thank you, Charles for your detailed answer.
1. What does me not feel at ease with ICC is that after having calculated the ICC value and the 95% confidence interval I find no way of interpreting rationally the results, which is of course essential for myself and the jury who is concerned.
I read your answer to Sravanti on July 24, 2015: there is no agreement as to what is an acceptable value for ICC, although you have typically seen .7 used. So what to do if ICC “medium big”
Phi Square = .16 > “big”
A from phi square derived parameter is eta square = phi square/(phi square +1) with a range [0;1]. It looks like a correlation coëfficiënt and its estimator gives an impression of the relative size of the effects of the factors and combination of factors in a Variance Analysis. So an effect is “small” for eta square = .010, “medium big” for eta square = .059, and “big” for eta square = .138
Wouldn’t there be a way of transposing to ICC?
Thank you once more
Erik
Erik,
I agree with you. These measurements seem most valuable when they show a problem or when they are very high. Middle values seem less useful.
Charles
Thank you Charles. There is no need to worry about your delayed answer. I hope you are fine and I needed anyway more time to understand…
I struggled further through the matter and realize that my questions in the beginning were not always very adequate.
The state of affairs for me is now as follows:
1. After having defined the appropriate statistical model one calculates an ICC which is an estimate of the population mean value rho of a very great number of samples take in identic conditions.
2. How to interprete this ICC value? It remains an open question to me since
there is no agreement about.
Wouldn’t it be logic to only consider lower limit of the confidence interval?
3. I believe that even the confidence interval, say 95%, relative to that estimate can be questionned. Since that interval is calculated round a one time estimate of rho it can either contain rho or not. Are those chances equal to 95% if you cannot repeat an experience a great number of times?
I begin to wonder if ICC calculations are suited for Case 2 wine tastings.
The example I gave you comes from following book (pg 244-247):
Wines Their sensory Evaluation by
Maynard A. Amerine and Edward B. Roessler
1976, 1983 by W.H. Freeman and Company
This is the data table:
Judge W1 W2 W3 W4 W5
1 8 4 2 5 4
2 6 4 5 6 5
3 6.5 3 8.5 7 5.5
4 3 4 5 6 7
5 8 7 5.5 8 6.5
6 3 3.5 7 9 8
7 7.5 5 4.5 5.5 8.5
Erik
Erik,
How to interpret the ICC value: Generally this statistic is used as a measurement of the agreement between raters. I still don’t completely understand the problem here.
Confidence Interval. I agree that only the lower bound may be of interest.
Regarding the issue of basing the confidence interval only on one sample, this is the usual situation not just for ICC but for confidence intervals of all sorts of statistics (t tests, regression, etc.). Our goal is to measure our confidence of the value of a specific population parameter based on the corresponding statistic from one sample. Since we only have one sample we can’t be certain of the value of the population parameter, but the larger the sample the narrower the confidence interval, and so the more confident we are in its value.
Case Wine Tasting: Why do you believe that the ICC calculations are not suited to this example?
Charles
I forgot to write in the text of my first question that I referred to example 1 in your Intraclass Coorelation chapter (Four colums for the judges and eight rows for the wines).
Erik
Charles,
I read the article “SF” and I wonder if what I understood is correct:
Say Rho(2,1) is the population mean of all ICC’s between the single scores related to a given situation. When the null Hypothesis Ho says rho is equel t0 zero, this is equivalent to saying: the mean square expectation between wines = 0, the mean square expectation between judges and/or the residual mean square expectation being different from zero.
ICC(2,1) is an estimate of rho(2,1) and when that ICC-value lies in the 95% confidence area we conclude at the 95% level of confidence that the judges have been consistent.
Question: Consistancy of a rater does not necessarily mean reliability nor give birth to agreement between raters. What does the ICC exactly assess?
I met an example (out of a book) that puzzles me a lot:
Seven judges rated five wines and this is the result two-way ANOVA showed:
– F wines < F critic .5: we accept Ho of no significant differences between the means of the wine scores.
– F judges < F critic .5: we accept Ho of no significant differences between the means of the judges' scores. The judges are consistent in their scoring.
– ICC(2,1) value equal to .118 (!) and confidence interval -.06 and .68. The ICC thus lies in the non significant zone. There too, can we simple conclude the judges are consistant?
Question: Looking at the correlations of the judges' scores this is so unlikely. How to interprete what figures show exactly?
Please give me your view on those two items?
And again: thank you very much
Erik
Erik,
Sorry for the delayed response.
As the Shrout and Fleiss article says ICC measures reliability. On page 425, they make a distinction between consistency of ratings using ICC(3,1) and agreement of ratings using ICC(2,1).
An ICC(2,1) of .118 indicates a low level of agreement between the judges. Since zero lies in the confidence interval of (-.06, .68), we need to reject the null hypothesis that there is agreement between the raters. I can’t comment on whether this is unlikely since I don’t have access to the data.
Charles
Hi Charles,
What does the negative values for lower band in CI95% tells us!
icc 0.6 (95% CI= lower= -0.0; upper= 0.8).
Thank you.
If the lower bound is -0.0, as in your example, then this likely means a very small negative number. In any case, when a statistic takes a range of value of say 0 to 1 and the lower confidence value is negative, it should be viewed as zero.
Charles
Hi Charles!
this is the result of a ICC test. I will appreciate it if you let me know if the Confidence interval is narrow enough to come to any conclusion.
ICC = .87(CI 95%=.466-.997),F(2,34) = 7.7, p < .005
best regards
Behrouz
Obviously the narrower the better, but I would say that you have a pretty good level of confidence that there is agreement among the raters. (As always, there is some risk that this is less so.)
Charles
Hello Charles,
My objective is to compute intraclass coefficient. I want to assess the degree of agreement between raters on the items of a new proposed tool. The tool is a 5 point Likert rated tool. There are two set of rater, Rater group 1 has psychologists (2 of them) and Rater group 2 has Educators (3 of them). It is a fully crossed model.
My question is :
1) How do I interpret these results? I obtained an intraclass coefficient by use of SPSS 20.For the psychologist group, I obtained the coefficient of o.54 , 95% confidence interval, the lower bound .197 and upper bound.754. These are average measures. and 0.54 for the educator group coefficient of o.54 , 95% confidence interval, the lower bound .257 and upper bound.729
2) I am interested in the degree of agreement for each of the items of the tool. Isn’t this coefficient value an indicator of the overall scale?
Hello,
1. There isn’t agreement as to what is an acceptable value for ICC, although I have typically seen .7 used. Which such a small sample and therefore such large confidence intervals (.197, .754) and (.257, .729) it is pretty hard to derive a lot of meaning from the results, except that they seem significantly different from zero.
2. For one item, I would simply use the variance, but again with such a small sample, this is not going to tell you very much.
Charles
Hi! Charles,
How we calculate ICC with one way anova for teams with different no. of people in each team. From example cited above we can use it only when there are same no. of people in each team. Kindly help.
Thanks,
Sapnaa
Sapnaa,
The approach that I present is only valid for equaò group sizes. There are a number of techniques available for unequal group sizes. E.g. see http://digitalcommons.wayne.edu/cgi/viewcontent.cgi?article=1301&context=jmasm.
Charles
In figure 3 above, in cell K37 and K37 there is a reference to cell I28. As far as I can see this cell is empty. Can you inform me what should be the right reference?
I asume it has to refer to F, so the reference should be or I35 or K23. Correct?
Hi Carel,
The correct formulas in cells I36, I37, I38 and I39 are:
=I35/FINV(I31/2,I33,I34)
=I35*FINV(I31/2,I34,I33)
=(I36-1)/(I36+I32-1)
=(I37-1)/(I37+I32-1)
I will correct the references made in cells K36, K37, K38 and K39.
Thanks for catching this error.
Charles