Cohen’s Kappa Sample Size

Basic Concepts

We now show how to calculate the sample size requirements in the case where there are only two rating categories. First, we present an alternative, but equivalent, approach to calculating the standard error for Cohen’s kappa, namely

where n = sample size and

In the case where k = 2, we can express the standard deviation sd in terms of κ, p1, and q1, where p1 is the marginal probability that rater 1 chooses category 1 and q1 is the marginal probability that rater 2 chooses category 1. This is because

The minimum sample size is now given by

where z_γ = NORM.S.INV(γ) and sd₀ is the standard deviation when the null hypothesis is true (i.e. when κ = κ₀) and sd₁  is the standard deviation when the alternative hypothesis is true (i.e. when κ = κ₁).

Often we want to determine the sample size that discriminates between no agreement (κ = 0) and some higher level of agreement (e.g. κ = .5), although other comparisons are possible.

Example

Example 1: Suppose that rater 1, a psychologist, and rater 2, a psychiatrist, will determine which subjects from a certain prison population meet the DSM V criteria for bipolar disorder. Suppose too that based on past experiments the psychologist tends to find that 40% are bipolar and the psychiatrist tends to find that 50% are bipolar.

Determine the minimum sample size required to test the null hypothesis κ = .3 versus the alternative hypothesis κ = .5, assuming a significance level of .05 and power of 90%.

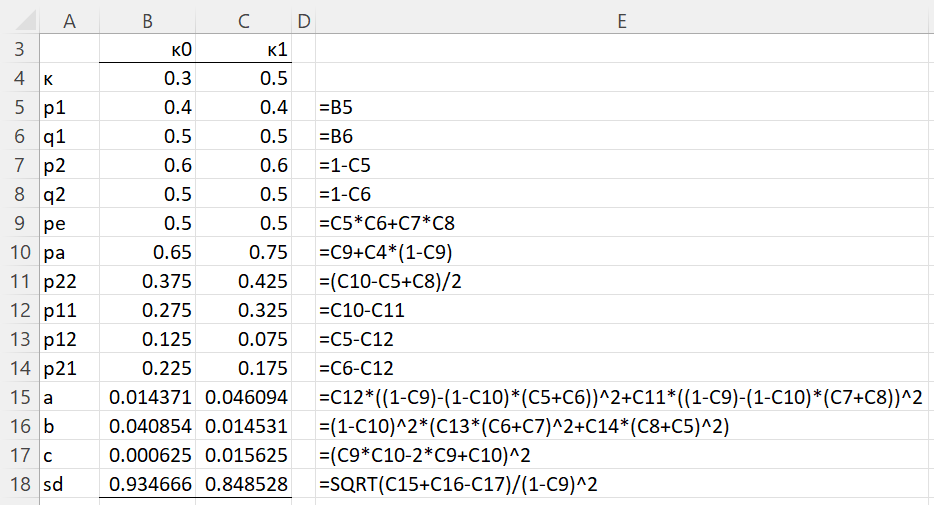
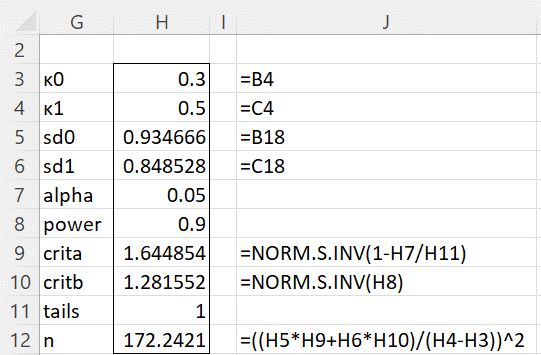
The calculation of the standard deviations for the two values of kappa is shown in Figure 1 (column E displays the formulas used in column C) and the resulting sample size is shown in Figure 2.

Figure 1 – Standard deviation calculation

Figure 2 – Sample size calculation

We see from Figure 2 that at least 173 prisoners need to be evaluated by the two raters.

Worksheet Functions

Real Statistics Functions: The Real Statistics Resource Pack contains the following array functions:

BKAPPA_SD(κ, p1, q1) = the standard deviation, sd, when κ = Cohen’s kappa, p1 = the marginal probability that rater 1 chooses category 1, and q1 = the marginal probability that rater 2 chooses category 1

BKAPPA_SIZE(κ0, κ1, p1, q1, pow, tails, α) = minimum sample size required to achieve power of pow  (default .80) when the null and alternative hypothesis kappa are κ0 and κ1, the marginal probabilities that rater 1 and rater 2 choose category 1 are p1 and q1, based on a significance level of α (default .05) and tails = 1 or 2 (default 2).

BKAPPA_POWER(κ0, κ1, p1, q1, n, tails, α) = statistical power achieved for a sample of size n when the null and alternative hypothesis kappa are κ0 and κ1, the marginal probabilities that rater 1 and rater 2 choose category 1 are p1 and q1, based on a significance level of α (default .05) and tails = 1 or 2 (default 2).

For Example 1, the standard deviation in cell B18 of Figure 1 can also be calculated by the formula =BKAPPA(B4,B5,B6). The sample size shown in cell H12 of Figure 2 can also be calculated by the formula =BKAPPA_SIZE(H3,H4,B5,B6,H8,H11,H7).

The actual power achieved when a sample of size 173 is utilized is 90.1188%, as calculated by the formula

= BKAPPA_POWER(H3,H4,B5,B6,INT(H12+1),H11,H7).

Data Analysis Tool

Real Statistics Data Analysis Tool: The Statistical Power and Sample Size data analysis tool can also be used to calculate the power and/or sample size. To do this, press Ctrl-m and select this data analysis tool from the Misc tab. On the dialog box that appears select the Cohen’s Kappa option and either the Power or Sample Size options.

See Real Statistics Power Data Analysis Tool for more information and examples.

Examples Workbook

Click here to download the Excel workbook with the examples described on this webpage.

References

Bujang, M. A. and Baharum, N. (2017) Guidelines of the minimum sample size requirements for Cohen’s Kappa. Biostatistics
https://riviste.unimi.it/index.php/ebph/article/view/17614

Cantor, A. B. (1996) Sample size calculations for Cohen’s kappa. Psychological Methods
https://www.ime.usp.br/~abe/lista/pdfGSoh9GPIQN.pdf

Fleiss, J. L., Cohen, J, Everitt, B. S. (1969) Large sample standard errors of kappa and weighted kappa. Psychological Bulletin
https://www.semanticscholar.org/paper/Large-sample-standard-errors-of-kappa-and-weighted-Fleiss-Cohen/f2c9636d43a08e20f5383dbf3b208bd35a9377b0