Bland-Altman Plot

Objective

Bland-Altman is a method for comparing two measurements of the same variable. This is especially important if you are trying to introduce a new measurement capability that has some advantages (e.g. it is less expensive or safer to use) over an existing measurement technique.

Example

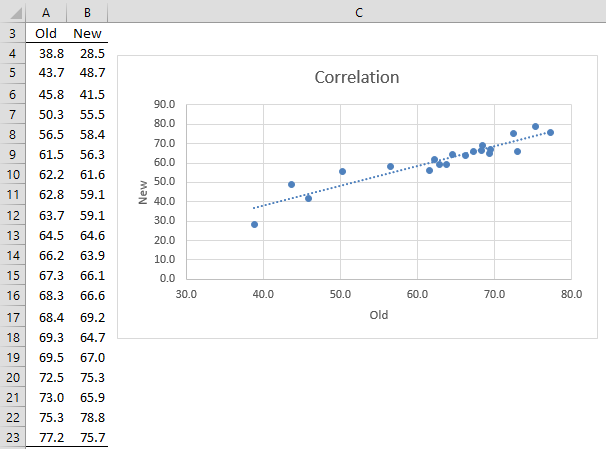
Example 1: A nuclear power plant has been using a fairly expensive method (Old) for measuring the strength of the rods in the nuclear reactor. The management team would like to implement a more cost-effective method (New), but first, they want to make sure there is agreement between the measurements done by these two methods. They do this by taking the measurements of 20 rods using both methods, as shown in Figure 1.

Comparing two measurements

Figure 1 – Comparison of two measurement instruments

As we can see from the scatter diagram on the right side of Figure 1, there is a high degree of correlation between the two methods. In fact, using the worksheet formula =CORREL(A4:A23,B4:B23), we see that the correlation coefficient is .903678.

But, it is important to note that correlation is not the same as agreement. In fact, if we double the data values in column B, the correlation would remain at .90, but we would clearly not have agreement between the two measurements.

Bland-Altman Plot

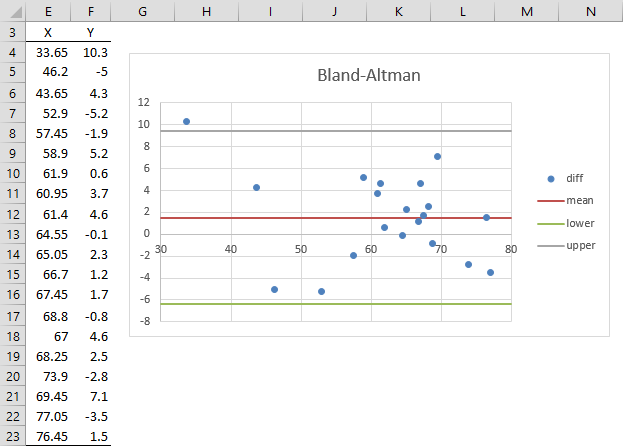
In order to more readily see the difference between the two measurement instruments, it is useful to plot the means of each pair of measurements (x value) versus the difference between the measurements (y value). This is called a Bland-Altman Plot, and is shown in Figure 2.

Bland-Altman Plot

Figure 2 – Bland-Altman Plot

We obtain the values in columns E and F by inserting the formula =(A4+B4)/2 in cell E4 and inserting =A4-B4 in cell F4, and highlighting the range E4:F23 and pressing Ctrl-D. Highlighting range E4:F23, we then select Insert > Chart|Scatter to create the scatter plot shown on the right side of Figure 2. We will explain the horizontal lines shown on the Bland-Altman Plot shortly.

Limits of Agreement

If there is agreement, we would expect the values in Figure 2 to cluster around the mean of the differences (called the bias). In fact, we would expect these values to be within 2 standard deviations of the mean. Assuming the differences are normally distributed, this would result in a 95% prediction interval

image094x

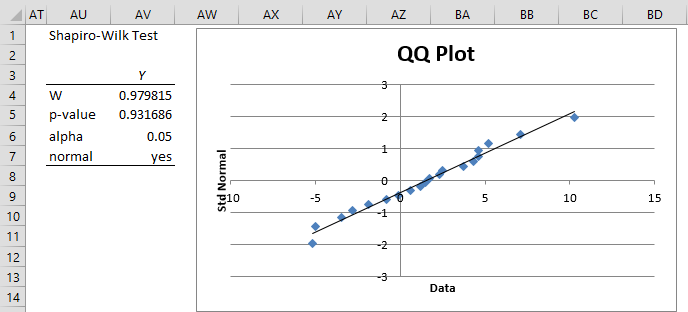
called the limits of agreement, where, as usual, \bar d = AVERAGE(F4:F23), sd = STDEV.S(F4:F23) and 1.96 = NORM.S.INV(.975). That the differences are normally distributed is actually quite likely. For this example, we can use the Real Statistics Descriptive Statistics and Normality data analysis tool on the data in range F4:F23 (i.e. the difference values) to check that the normality assumption does indeed hold, as shown in Figure 3.

Normality test Bland-Altman

Figure 3 – Shapiro-Wilk and QQ Plot tests for normality

As we can see from Figure 2, only one out of the 20 points lies outside the limits of agreement, with the points scattered within the limits of agreement.

Calculation of the Limits of Agreement

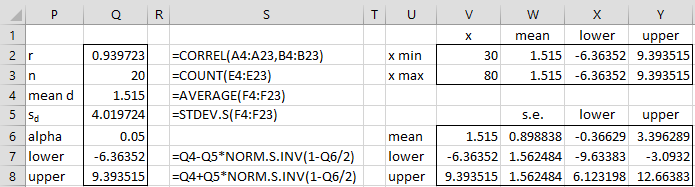
The left side of Figure 4 shows the calculation of the mean and limits of agreement.

Bland Altman agreement levels

Figure 4 – Calculation of Mean and Limits of Agreement

We see from Figure 4 that \bar d = 1.515 (cell Q4) and the limits of agreement are -6.36352 (cell Q7) and 9.393515 (cell Q8).

The standard error in cell W6 is calculated by the formula =Q5/SQRT(Q3). We calculate the standard error shown in cells W7 and W8 by the formula

=SQRT((1/Q3)+NORM.S.INV(0.975)^2/(2*(Q3-1)))*Q5

Cell X6 contains the formula =V6-W6*T.INV.2T(0.05,Q3-1) (and similar formulas for the other cells in range X6:Y8).

Note that the x values for the scatter plot in Figure 2 range from 30 to 80, and so we specify in range V2:Y3 of Figure 4 the endpoints for the three horizontal lines (for the mean and lower and upper limits) shown in Figure 2. We add these horizontal lines to the scatter diagram by adding three series to the scatter diagram data, as described in Limits of Agreement for Bland-Altman Plot.

Interpretation

Whether we accept the new measurement instrument or not depends on the level of precision that is needed in a particular domain. In fact, for this application, 2 standard deviations of difference is too much. Since the range of differences between the new and old measurements is pretty high, for this sensitive an application we decide not to use the new measurement instrumentation.

The points in Figure 2 are pretty spread out over the limits of agreement. If instead the points were congregated around say the horizontal line y = 3.0, then we could conclude that the new instrumentation is acceptable provided we correct these measurements by adding 1.485 (i.e. 3.0 – 1.515).

Examples Workbook

Click here to download the Excel workbook with the examples described on this webpage.

References

Giavarina, D. (2015) Understanding Bland Altman analysis. Biochemia Medica
https://www.ncbi.nlm.nih.gov/pmc/articles/PMC4470095/

Bland, J. M. and Altman, D. G. (1986) Statistical methods for assessing agreement between two methods of clinical measurement. Lancet, 1986 pp 307-310
https://pubmed.ncbi.nlm.nih.gov/2868172/

48 thoughts on “Bland-Altman Plot”

  1. my data is non parametrically distributed. can I still use a bland altmon plot. if yes, is there a different way I need to do it or the same

    Reply

  2. Dear Dr Zaiontz,

    Is it appropriate to plot a Bland-Altman difference plot if two DNA PCR assays under comparison have different reporting units, and there isn’t a conversion factor to convert one to the other? For example, one PCR assay reports results in copies/ml and the other reports results in international unit/ml (IU/ml).

    Many thanks.

    Kind regards,
    Ian

    Reply

      • Hi Charles,

        I tried to log transformed the values (cp/ml for method A and IU/ml for method B) and plot a BA difference plot, but I am not sure the meaning of the comparison/difference between the methods (due to different units) and I think it’s inappropriate to compare them to draw any meaningful conclusion. Thoughts?

        Reply

          • Thanks Charles, that’s what I thought but one of the reviewers think it is appropriate to compare the mean difference of two different PCRs though one is reported in copies/ml and the other is reported in IU/ml.

  3. Great application! Do you have any examples of BA with absolute values on the x-axis rahter than average? /Jacob Karlsson, Sweden

    Reply

  4. Hi Charles,

    Thanks for the great explanations. If my calculated stdev.s value is 0.07 (thus, lower than 2), but I still have two or three points outside the upper and/or lower horizontal bars (total n=60), thus outside the limits of agreement, can I say the two techniques in question are in agreement, and one measurement technique may theoretically be good to replace the other, and I’ve simply just got a few technical outliers that fell outside the limits of agreement?

    Thanks
    Bryan

    Reply

    • Hello Bryan,
      Ideally, you want all the points to be as close as possible to the mean line. The upper and lower limits are set at a traditional two standard deviations away from the mean (based on a normal distribution). Depending on the precision required by your application you can set a narrower or wider limit. If you have lots of points, then you could expect a few to be outside the limits (outliers), but with a small number of points, you should expect all the points to be within the limits. Again, depending on the precision required you can accept fewer or more outliers.
      Charles

      Reply

  5. hi Charles, this is a great website. thank you.

    How do I draw the mean, upper and lower limits on my graph? I have worked out these values using your formula.

    Reply

    • Hello May,
      Thank you for your kind remarks about the website.
      How to add the mean and upper/lower limits is described on this webpage towards the bottom, just above the last two Observations.
      You can also see the results in Reliability examples workbook. See
      Examples Workbooks
      Charles

      Reply

  6. I just installed your RealStats app as I need to make some Bland-Altman Plots but I want to look at the mean vs. % difference, as the biomedical data I’m looking at has a 3 log unit range so just looking at the absolute differences is not very useful. Is there anyway of using the app to look at % difference?

    Reply

    • Hi Nicholas,
      The two measurements that are being compared need to measure the same thing. As long as this is the case, you can use Bland-Altman. If you want to do the comparison in another way, perhaps Lin’s CCC, Deming regression or Passing-Bablok regression would fit your needs better. These are explained on the website.
      Charles

      Reply

      • Hi Charles
        There is new draft guidance from the ICH (M10) and they request Bland-Altman Plots when comparing 2 bioanalytical methods. Basically the same sample is analyzed using the 2 methods. In the past the preferred method was to calculate the mean of the 2 results and the % bias from the mean (for one set of data) then acceptance criteria of +/- 20% for at least 67% of the samples is used. For me the Bland-Altman gives some good data on the overall bias the assays. The problem is using absolute values is not very useful as the assay range is so large (a +/- 1.96SD of 5 is OK at 100 ng/mL but meaningless at 0.1 ng/mL) so it is better to use % difference from the mean. I have made an excel to do the calculations but I like your APP so wanted to see if I have missed an option to see the % difference.

        Reply

  7. Since the range of differences between the new and old measurements is pretty high (i.e. 2 standard deviations of different is too much).

    I see that SD=4.02. So in the above sentence, y 2 standard deviation difference what do you mean? I didn’t get that. Please explain!

    Thank you!

    Reply

    • Since sd = 4.02 is much higher than 2, we conclude that it is unlikely that we have agreement. Note that for a normal distribution the interval between mean minus 2 standard deviations (i.e. sd = 2) and mean plus 2 standard deviation is equivalent to about 95% of the probability; i.e. less than mean-2*sd has probability 2.5% and more than mean+2*sd has probability 2.5% (for a total of 5%). This is the typical significance level of alpha = 5% used in statistics.
      Charles

      Reply

  8. Is there a difference between standard error (s.e.) and standard error of measurement (SEM)? or it’s the same? If it’s different, please explain the difference!

    Thank you!

    Reply

    • Yes Miguel, you are correct. Thank you for identifying this error. I have now corrected the webpage. I appreciate your help in improving the website.
      Charles

      Reply

  10. HI Charles,

    Can I use this technique to illustrate one method is comparable with another? I am trailing a new analytical method along side our current method. there is 150 different samples ranging from 0-10 being measured on each method once.

    Reply

  12. Dear sir,
    could you explain final part of mean lower uper limiit standard eror calculation part.
    i am not able clear in this , i want to analysis my data for comparison please kindly send if any to available a tools available.
    Thankyou

    Reply

    • Rajavelu,
      The standard error in cell W6 is calculated by the formula =Q5/SQRT(Q3), that in cell W7 and W8 by the formula =SQRT((1/Q3)+NORM.S.INV(0.975)^2/(2*(Q3-1)))*Q5. Cell X6 contains the formula =V6-W6*T.INV.2T(0.05,Q3-1) (and similar formulas for the other cells in range X6:Y8).
      Charles

      Reply

  13. Hi Mr. Charles
    could you please explain how do you find the x min 30 and x max 80
    if I have data like ( 3261.42 ,, 3528.68 ,, 3635.36 ,, 3784.42 ,, 3921.18 ,, 4048.83 4143.26 ,, 4221.28 ,, 4295.80 ,, 4329.09 ) how I can calculate the x min and max

    thank you

    Reply

    • Moayed,
      The min is 33.65 and the max is 77.05. I simply rounded these values to 30 and 80. You can take any values lower than the actual min and higher than the actual max.
      Charles

      Reply

  15. Hi Charles,
    I believe that I may have found an error in your spreadsheet formula for s.e. of lower/upper limit. Your web page states the formula as:
    s.e. of lower/upper limit = sd * SQRT(1/n + (1.96)^2/(2*(n-1)))
    But your formula in the spreadsheet for W7 and W8 and in the RealStats app has the formula implemented as: sd * SQRT(1/n + (1.96)^2/(2*n-1))
    I calculate that W7 and W8 should be 1.562484 instead of 1.549023. This error also propagates into cells X7, X8, Y7, and Y8. Please check these formulas and help me understand which formula is the correct version. Thanks for providing such a great resource!
    Jeff

    Reply

    • Jeff,
      Thanks for catching this error. I have now corrected the webpage. The Real Statistics data analysis tool has also been corrected. The corrected version will be available later today in Rel 5.6.
      I really appreciate your help in improving the website and software.
      Charles

      Reply

  16. Hi,
    I have followed through your method with my data and found that it is not normally distributed. How will this affect by analysis and use of Bland-Altman?
    Many thanks

    Reply

    • Sarah,
      Not everything on the webpage depends on the normality assumption, however, the limits of agreement does depend on this assumption. Note that it is the differences that need to be normal and not the two sets.
      If this assumption doesn’t hold, then the accuracy of the limits of agreement really depends on how far off from normality the differences are.
      Charles

      Reply

  17. Hi. Can the Bland-Altman analysis be used in test-retest reliability? Like when a measurement (scale) is tested two times with 3-week interval?

    Thank you for the response.

    Reply

  18. Hi Charles

    How do you calculate the s.e. and the upper and lower limits in the cells w x and y….

    Sorry I am not a excel expert in any way…..

    Reply

  19. hi charles
    please can you show the formulas for calculation of w7:w8 cells??
    i replied your calculation form with same numbers, and i read the “confidence interval for bland-altman” page.
    when i apply the formula for the standard error for agrrement limits, but result is different from 1.549023. other results are ok, also s.e. for mean (cell w6)

    have you explained on the site the procedure for shapiro-wilk test???

    a very useful job
    thank you !
    giovanni

    Reply

    • The formulas that are used are shown in column S. Unfortunately, the formulas that were previously shown were not correct (actually they were not updated after I made some changes). I have now corrected this mistake.
      Thanks for asking your question. It enabled me to see that there was an error and so helped improve the website. I trust that the revised information answers your question.
      Charles

      Reply

Leave a Comment