Basic concepts
The Spearman-Brown correction is a specific form of the Spearman-Brown predicted reliability formula. Suppose we have a test with reliability ρ. The reliability ρ′ of the test replicated n times is given by the formula
When n = 2, we have the Spearman-Brown correction for halves of equal length (as described in Split-Half Basic Concepts).
Alternative approach
Another way to view the Spearman-Brown formula is as follows: suppose that the reliability for a test with m items is ρ, then a test with mn items will have reliability ρ′.
Now suppose that the reliability of a test is ρ = .2 and suppose we have 5 such units (i.e. n = 5), then![]()
If n is increased to 10, then ρ′ = .714 and if n = 50, then ρ′ = .926. We see that the larger the number of units, the larger the reliability.
In fact, we can solve the above equation for n to determine how many units are required to achieve any specified reliability target (provided we know the value of ρ).
Thus, if our goal is to achieve reliability of .75 we would need
Thus, we would need a sample with 12 units to achieve the total reliability target.
Example
Example 1: Suppose that the split-half reliability is .5 based on a test with 12 questions. What will the predicted reliability be if you have 24 (comparable) questions? How many questions to you need to have to get a predicted reliability of .80?
First, we solve the Spearman-Brown predicted reliability formula for ρ as follows:
ρ represents the reliability for one test unit (i.e. one question for this example).
Substituting the values ρ′ = .5 and n = 12, we get
Now we can calculate ρ′ using the Spearman-Brown predicted reliability formula when ρ = .0769 and n = 24.
To achieve a predicted reliability of .80, we use the following approach
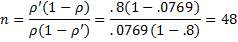 Worksheet Functions
Worksheet Functions
Real Statistics Functions: The Real Statistics Resource Pack contains the following functions:
SB_PRED(m, rho, n) = Spearman-Brown predicted reliability based on m items when Spearman-Brown for n items is rho.
SB_SIZE(rho1, rho, n) = the number of items necessary to bring the Spearman-Brown predicted reliability up (or down) to rho1 from n items with Spearman-Brown of rho
We can get the answers for Example 1 by using the following formulas:
SB_PRED(24, .5, 12) = .667
SB_SIZE(.8, .5, 12) = 48
Halves of unequal length
The Spearman-Brown predicted reliability formula takes the following form when the two halves are not equal in length.
Property 1: Where p = the proportion of the test due to the first half and c = 2p(1–p), the Spearman-Brown correction factor can be expressed as
Proof: Click here
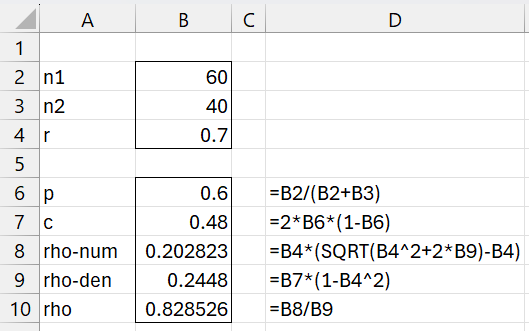
Example 2: Calculate rho for values in range B2:B4 of Figure 1.
Figure 1 – Spearman-Brown predicted reliability
We see from Figure 1 that ρ = .8285.
Examples Workbook
Click here to download the Excel workbook with the examples described on this webpage.
References
Wikipedia (2016) Spearman-Brown prediction formula
https://en.wikipedia.org/wiki/Spearman%E2%80%93Brown_prediction_formula#:~:text=The%20Spearman%E2%80%93Brown%20prediction%20formula,after%20changing%20the%20test%20length.
Horst, P. (1951) Estimating total test reliability from parts of unequal length
https://journals.sagepub.com/doi/10.1177/001316445101100306
Gebotys, R. (2003) Handout on reliability
https://studylib.net/doc/8088080/reliability-analysis
Nydick, S.W. (2012) The relationship between Spearman-Brown and Cronbach’s alpha
https://swnydick.github.io/assets/reports/Spearman_Brown_and_Coefficient_Alpha.pdf
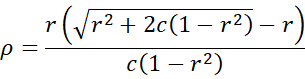
thanks for what you have done.