Cronbach’s Alpha Hypothesis Testing

Hypothesis Testing

Property 1: If the value of Cronbach’s alpha based on a sample of size n with k items is γ, then for any γ0, the statistic W has the following distribution:

image9178

If we want to test the null hypothesis that (the population value of) Cronbach’s alpha is less than some value γ0 we check whether the p-value of W is less than alpha (i.e. the significance level). In this case, we reject the null hypothesis that Cronbach’s alpha < γ0. If we want to test whether Cronbach’s alpha > γ0 then we use a p-value of 1 – the p-value of W.

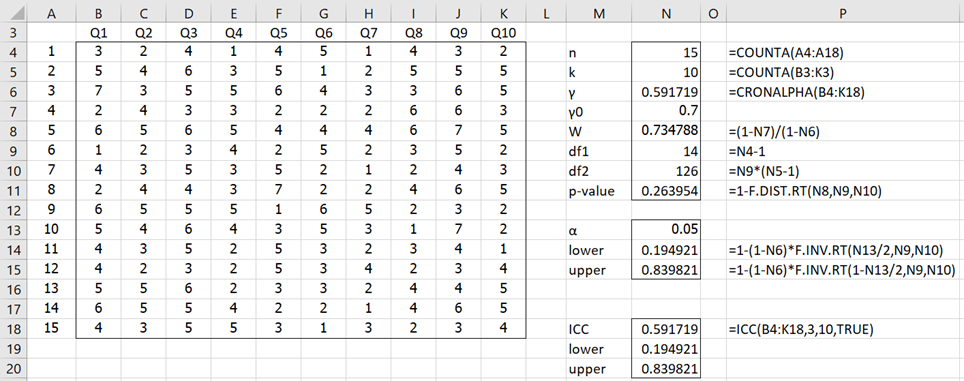
Example 1: Test whether the value of Cronbach’s alpha in Example 4 of Cronbach’s Alpha is at least .7.

The hypothesis test is shown in Figure 1.

Cronbach's alpha hypothesis testing

Figure 1 – Hypothesis test for Cronbach’s alpha

We see from Figure 1 that p-value = .26 > .05 = α, and so we cannot refute the null hypothesis that Cronbach’s alpha is at least .7.

Confidence Intervals

Using Property 1, an estimate of the 1–α confidence interval for Cronbach’s alpha based on a sample of size n with k items where Cronbach’s alpha of the sample is γ is given by (γL, γU) where

Cronbach's alpha confidence interval

Cronbach's alpha CI right

For Example 1, this results in a 95% confidence interval of (.195. 840), as shown in cells N14 and N15. As you can see, the width of the confidence interval = .840 – .195 = .645, which is quite wide.

For a one-tailed test on the left side, the confidence interval is (γL, 1) where γL is as above except that α/2 is replaced by α. For a one-tailed test on the right side, the confidence interval is (-1, γU) where γU is as above except that α/2 is replaced by α.

Worksheet Function

Real Statistics Function: As described in Other ICC Models, the ICC(R1, 2, 1, TRUE, α) array formula (where R1 contains the data) can be used to output a range that contains Cronbach’s alpha and the lower and upper confidence interval values.

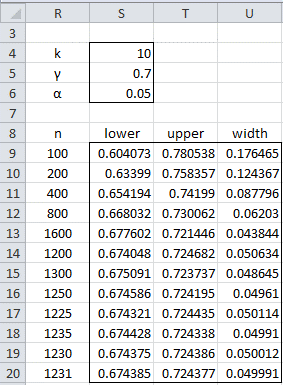
Example 2: If you expect Cronbach’s alpha to be .7 for a 10-question test, how big a sample do you need so that your confidence interval is no wider than .05?

Here we are asking the question, “What is the minimum value of n so that γU – γL < .05?” We can find this value using Excel’s Goal Seek capability. This time, however, we will find the value of n by trial and error (with a little bit of intelligence), as shown in Figure 2.

Sample size for CI width

Figure 2 – Sample size to achieve confidence interval width

This approach works since the larger the value of n the smaller the confidence interval width. As we can see from Figure 2, the required sample size is 1,230.

Examples Workbook

Click here to download the Excel workbook with the examples described on this webpage.

References

Hintze, J. L. (2015) Tests for coefficient alpha. NCSS PASS
https://www.ncss.com/wp-content/themes/ncss/pdf/Procedures/PASS/Tests_for_One_Coefficient_Alpha.pdf

Hintze, J. L. (2015) Confidence intervals for coefficient alpha. NCSS PASS
https://www.ncss.com/wp-content/themes/ncss/pdf/Procedures/PASS/Confidence_Intervals_for_Coefficient_Alpha.pdf

12 thoughts on “Cronbach’s Alpha Hypothesis Testing”

  1. Hello Charles
    If you want to prove that Cronbach alpha is significantly less than 0.7, what do you do the the equations
    P11
    P14
    P15
    I took out the (1-xxxxx) and ended up with a p value of 0.06 which surprised me as I thought a 0.35 Cronbach alpha would be significantly less than 0.7
    Also are the CI different for the < argument
    thanks
    Chris

    Reply

  2. Hello why I am getting W value of 2.12 in testing hypothesis with Cronbach alpa when the statistic W should be between 0 and 1?

    Reply

  3. Hi, I’m having so much difficulty on my research subject can you make a samples of reliability test through cronbach alpha in my research title EFFECTS OF SALES PROMOTION ON PURCHASING DECISION OF CONSUMER with 20 respondents

    Reply

  4. Charles: This is fabulous. Thank you so much for this effort.
    I am trying to calculate Cronchbach’s alpha. I am getting value to 0.18 and some negative values (i understand that means order is reversed)

    I am not getting p value or CI which you mentioned in above picture. I am computing via internal consistency reliability.

    Reply

  5. Dear Charles
    Which formula we can use for calculating cronbach alpha through MS Excel………….. i searched but unable to get ……… Pls help

    Reply

  6. Dear Charles,
    I entered data (γ0, γ1, k, pow, tail, α) = (0.6, 0.65, 80, 0.8, 2, 0.05), the program error is “A tremor time error has occurred. Select the gain. Unable to FINV get the property of the WorksheetFunction class”.
    Is the number of items (80) too big? Thanks.

    Reply

    • Dear Dung,
      No, 80 is not too big. I believe there is a bug in the software.
      I see that CALPHA_POWER(.6,.65,878,80,2,.05 = .800052 and CALPHA_POWER(.6,.65,877,80,2,.05) = .799617. Thus the sample size should be n = 878.
      This will be resolved in the next release of the software, but for now you can use the CALPHA_POWER function to make successive approximations of the sample size.
      Thanks very much for identifying this problem.
      Charles

      Reply

Leave a Comment