Cronbach's Alpha Concepts | Real Statistics Using Excel

Basic concepts

One problem with the split-half method is that the reliability estimate obtained using any random split of the items is likely to differ from that obtained using another. One solution to this problem is to compute the Spearman-Brown corrected split-half reliability coefficient for every one of the possible split-halves and then find the mean of those coefficients. This is the motivation for Cronbach’s alpha.

Cronbach’s alpha is superior to Kuder and Richardson Formula 20 since it can be used with continuous and non-dichotomous data. In particular, it can be used for testing with partial credit and for questionnaires using a Likert scale.

Definition

Definition 1: Given variable x₁, …, x_k and x₀ = $\sum\nolimits_{j=1}^k x_k$ and Cronbach’s alpha is defined to be

Property 1: Let x_j = t_j + e_j where each e_j is independent of t_j and all the e_j are independent of each other. Also let x₀ = $\sum\nolimits_{j=1}^k x_j$ and t₀ = $\sum\nolimits_{j=1}^k t_j$ . Then the reliability of x₀ ≥ α where α is Cronbach’s alpha.

Here we view the x_j as the measured values, the t_j as the true values and the e_j as the measurement error values. Click here for a proof of Property 1.

Observation: Cronbach’s alpha provides a useful lower bound on reliability (as seen in Property 1). Cronbach’s alpha will generally increase when the correlations between the items increase. For this reason the coefficient measures the internal consistency of the test. Its maximum value is 1, and usually its minimum is 0, although it can be negative (see below).

Interpretation

A commonly-accepted rule of thumb is that an alpha of 0.7 (some say 0.6) indicates acceptable reliability and 0.8 or higher indicates good reliability. Very high reliability (0.95 or higher) is not necessarily desirable, as this indicates that the items may be entirely redundant. These are only guidelines and the actual value of Cronbach’s alpha will depend on many things. E.g. as the number of items increases, Cronbach’s alpha tends to increase too even without any increase in internal consistency.

The goal in designing a reliable instrument is for scores on similar items to be related (internally consistent), but for each to contribute some unique information as well.

Observation: There are an number reasons why Cronbach’s alpha could be low or even negative even for a perfectly valid test. Two such reasons are reverse coding and multiple factors.

Reverse Coding

Suppose you use a Likert scale of 1 to 7 with 1 meaning strongly disagree and 7 meaning strongly agree. Suppose two of your questions are: Q1: “I like pizza” and Q20: “I dislike pizza”. These questions ask the same thing, but with reverse wording. In order to apply Cronbach’s alpha properly, you need to reverse the scoring of any negatively phrased question, Q20 in our example. Thus if a response to Q20 is say 2, it needs to be scored as 6 instead of 2 (i.e. 8 minus the recorded score).

Multiple Factors

Cronbach’s alpha is useful where all the questions are testing more or less the same thing, called a “factor”. If there are multiple factors then you need to determine which questions are testing which factors. If say there are 3 factors (e.g. happiness with your job, happiness with your marriage and happiness with yourself), then you need to split the questionnaire/test into three tests, one containing the questions testing factor 1, one with the questions testing factor 2 and the third with questions testing factor 3. You then calculate Cronbach’s alpha for each of the three tests. The process of determining these “hidden” factors and splitting the test by factor is called Factor Analysis (see Factor Analysis).

Example with binary data

Example 1: Calculate Cronbach’s alpha for the data in Example 1 of Kuder and Richardson Formula 20 (repeated in Figure 1 below).

Figure 1 – Cronbach’s Alpha for Example 1

The worksheet in Figure 1 is very similar to the worksheet in Figure 1 of Kuder and Richardson Formula 20. Row 17 contains the variance for each of the questions. E.g. the variance for question 1 (cell B17) is calculated by the formula =VARP(B4:B15). Other key formulas used to calculate Cronbach’s alpha in Figure 1 are described in Figure 2.

Figure 2 – Key formulas for the worksheet in Figure 1

We see from cell B22 that Cronbach’s alpha is .73082, the same as the KR20 reliability calculated for Example 1 of Kuder and Richardson Formula 20.

Observation: If the variances of the x_j vary widely, the x_j can be standardized to obtain a standard deviation of 1 prior to calculating Cronbach’s alpha.

Impact of each question

To determine how each question on a test impacts the reliability, Cronbach’s alpha can be calculated after deleting the ith variable, for each i ≤ k. Thus for a test with k questions, each with score x_j, Cronbach’s alpha is calculated for $x^*_i$ for all i where $x^*_i$ = $\sum\nolimits_{j \neq i} x_j$ .

If the reliability coefficient increases after an item is deleted, you can assume that the item is not highly correlated with the other items. Conversely, if the reliability coefficient decreases, you can assume that the item is highly correlated with the other items.

Example 2: Calculate Cronbach’s alpha for the survey in Example 1, where any one question is removed.

The necessary calculations are displayed in Figure 3.

Figure 3 – Cronbach’s Alpha for Example 2

Each of the columns B through L represents the test with one question removed. Column B corresponds to question #1, column C corresponds to question #2, etc. Figure 4 displays the formulas corresponding to question #1 (i.e. column B); the formulas for the other questions are similar. Some of the references are to cells shown in Figure 1.

Figure 4 – Key formulas for worksheet in Figure 3

As can be seen from Figure 3, the omission of any single question doesn’t change the Cronbach’s alpha very much. The removal of Q8 affects the result the most.

Calculation using ANOVA

Another way to calculate Cronbach’s alpha is to use the Two Factor ANOVA without Replication data analysis tool on the raw data and note that:

Example 3: Calculate the Cronbach’s alpha for Example 1 using ANOVA.

We begin by running Excel’s Anova: Two Factor without Replication data analysis tool using the data in range B4:L15 of the worksheet shown in Figure 1.

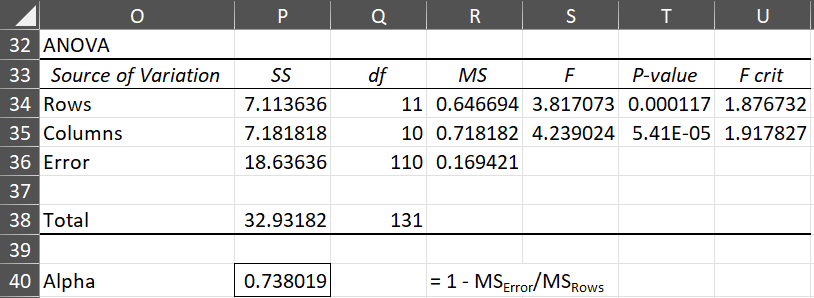
Figure 5 – Calculation of Cronbach’s alpha using ANOVA

As you can see from Figure 5, Cronbach’s alpha is .73802, the same value calculated in Figure 1.

Observation: Alternatively, we could use the Real Statistics Two Factor ANOVA data analysis tool, setting the Number of Rows per Sample to 1. We can also obtain the same result using the Real Statistics capabilities described in Real Statistics Support for Cronbach’s Alpha.

Examples Workbook

Click here to download the Excel workbook with the examples described on this webpage.

References

Tavakol, M., Dennick, R. (2011) Making sense of Cronbach’s alpha. International Journal of Medical Education
https://www.ijme.net/archive/2/cronbachs-alpha.pdf

Gliem, J. A., Gliem, R. R. (2004) Calculating, interpreting, and reporting Cronbach’s alpha reliability coefficient for Likert-type scales
https://scholarworks.indianapolis.iu.edu/server/api/core/bitstreams/976cec6a-914f-4e49-84b2-f658d5b26ff9/content

Newsom, J. (2017) Empirical estimates of reliability: Cronbach’s alpha
https://web.pdx.edu/~newsomj/pmclass/empirical%20estimates%20of%20reliability.pdf

Cronbach’s Alpha Basic Concepts