Motivation
Passing-Bablok regression is a non-parametric technique for comparing two methods (especially two measurement techniques) to see whether or not they yield similar results. This is also the motivation for Deming regression and Bland-Altman. Often you are comparing an existing method with some new method that has some advantages (less expensive, less-invasive, easier to apply, etc.), but you still want to make sure that the new method will produce similar results.
Ordinary linear or total least squares regression can be used for this purpose in which data from one method is regressed on data from the other to produce a linear regression model of the form y = βx + α. You then need to test the null hypotheses that the slope β = 1 and the intercept α = 0, in which case y = x, as desired.
Passing-Bablok regression is based on a similar motivation except that the normality assumption is dropped.
Steps
Passing-Bablok regression is performed on the data X = {x1, …, xn} and Y = {y1, …, yn} using the following steps:
Step 1: Calculate the slope of all possible pairs of XY points. There are N = C(n, 2) such pairs. More specifically, for the pairs (xi, yi) and (xj, yj) where j > i calculate the slope sij as follows:
We will then calculate the median of S = {sij: j > i} and use it as an estimate of the slope coefficient in the regression, although, as we will see shortly, we need to make a few modifications to this approach.
The first modification required is what to do when xi = xj, in which case sij is undefined. We handle this in the following ways:
- If xi = xj and yi = yj (in which case sij = 0/0), then exclude that sij from the set S.
- If xi = xj and yi < yj (in which case sij = ∞), set sij = L where L is a large positive number (the exact value won’t figure into the calculation of the median of S)
- If xi = xj and yi > yj (in which case sij = -∞), set sij = –L where L is a large positive number (again, the exact value won’t figure into the calculation of the median of S)
In addition, we make the following modification:
- If sij = -1, then exclude that sij from the set S.
Step 2: We next set k equal to the number of elements in S that are less than -1. Instead of setting the regression slope coefficient to the median of S we set it to the median shifted k places to the right.
More specifically, if S contains M elements (i.e. N elements minus the elements that have been removed), then if M is odd, namely M = 2m+1, then the median is the m+1th smallest element in S, and so we set the regression slope coefficient b = the m+1+kth smallest element in S.
If instead, M is even, namely M = 2m, then the median is the average between the mth smallest element in S and the m+1th smallest element in S, and so we set the regression slope coefficient b equal to the mean of the m+kth and m+1+kth smallest elements in S.
Note that in Excel, we will use the SMALL function to carry out these calculations.
The intercept coefficient a is now equal to the median of the set {yi – bxi: 1 ≤ i ≤ n}.
Step 3: We calculate a confidence interval for the regression coefficients as follows. Define
where zcrit = NORM.S.INV(1–α/2) and define
m1 = (N – c)/2 rounded off to the nearest integer
m2 = N – m1 + 1
The confidence interval for the slope coefficient is (blower, bupper) where
blower is the m1+kth smallest element in S
bupper is the m2+kth smallest element in S
The 1–α confidence interval for the intercept coefficient is (alower, aupper) where
alower is the median of {yi – bupperxi: 1 ≤ i ≤ n}
aupper is the median of {yi – blowerxi: 1 ≤ i ≤ n}
Step 4: If 1 is contained in the confidence interval for the slope and 0 is contained in the confidence interval for the intercept, then we have confidence in the similarity between the two methods. Note that since we have two tests, it would be prudent to use a Bonferroni correction (e.g. by replacing alpha = .05 by alpha = .05/2 = .025). Keep in mind that some would accept 90% confidence (or even higher) rather than 95% confidence.
Example
Example 1: An existing measurement technique was used to obtain the measurements for 18 subjects shown in column B of Figure 1, while the corresponding measurements for these subjects based on a new technique are shown in column C. Using Passing-Boblok regression 1, determine whether the measurements from the new technique are sufficiently similar to those from the existing technique.
Note that the data are the same as those used for Example 1 of Lin’s CCC.
Figure 1 – Passing-Boblok Regression (part 1)
We start by creating an 18 × 18 array containing the sij values. To do this, we first place the array formula =TRANSPOSE(B4:C22) in range D2:V3. We next insert the following formula in cell E5
=IF($D5>E$4,IF($B5<>E$2,IF($B5+$C5<>E$2+E$3,($C5-E$3)/($B5-E$2),””), IF($C5>E$3,1000,IF($C5<E$3,-1000,””))),””)
and then highlight range E5:V22 and press Ctrl-R and Ctrl-D. In this formula, we have used 1000 as a large positive value (the L in the description of the P-B regression procedure).
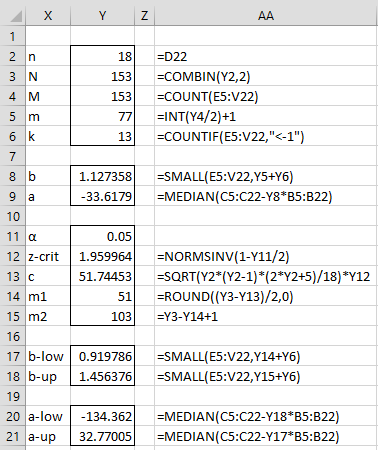
We continue building the spreadsheet as shown in Figure 2. Here the formulas in cells Y9, Y20, and Y21 are array formulas.
Figure 2 – Passing-Boblok Regression (part 2)
We see that the slope coefficient is b = 1.127 with 95% confidence interval (.92, 1.49), while the intercept coefficient is a = -33.62 with 95% confidence interval (-142.8, 32.8). Since 1 is included in the confidence interval for the slope and 0 is included in the confidence interval for the intercept, we conclude that the new technique yields sufficiently similar measurements to the existing technique.
The one proviso is that we must also check to make sure that the linearity assumption holds.
Examples Workbook
Click here to download the Excel workbook with the examples described on this webpage.
References
Hintze, J. L. (2020) Passing-Bablok regression for method comparison. NCSS
https://www.ncss.com/wp-content/themes/ncss/pdf/Procedures/NCSS/Passing-Bablok_Regression_for_Method_Comparison.pdf
Passing, H. and Bablok, W. (1983, 1984) Comparison of several regression procedures for method comparison studies and determination of sample sizes. Application of linear regression procedures for method comparison studies in Clinical Chemistry. J. Clin. Chem. Clin. Biochem
https://pubmed.ncbi.nlm.nih.gov/6481307/
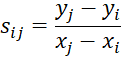

Hi Charles,
I want to use your 2 data sets. How will i cite you 🙂
Regards
Hi Steve,
See https://real-statistics.com/appendix/citation-real-statistics-software-website/
Charles
Thx so far Charles
hi charls can you please explain how to do it on spss
Sorry, but I don’t use SPSS.
Charles
Hi Charles, thanks for the tuto
I just have a question, for the calculation of parameter c :
=RACINE(Y2*(Y2-1)*(2*Y2+5)/18)*Y12
I don’t really understand where the 18 come from ? is it related to the array size (18×18). Also I don’t understand if the 5 is a constant value ?
Thanks so much
Hello Mat,
I am not familiar with the RACINE function. What is this?
Charles
Hi sorry,
It is SQRT (RACINE in french)
Thanks
Mat
Mat,
5 and 18 are just constants. They don’t change with the array size. You would need to read the original papers to find out why these constants are used.
Charles
Charles,
Thanks for your response. Yes I am going to read the original paper !
Mat
Hello, Charles,
I have tried to recalculate your example of PB (in Excel 2019); data in my sheet looks identical to Figure 1, but the results for =median() are different in comparison to Figure 2, namely
a=-17.90, a-low=-196.047, a-up=50.2193. Any idea?
n 18
N 153
M 153
m 77
k 13
b 1.127358491
a -17.9009434
alpha 0.05
z-krit. 1.959963985
c 51.74453399
m1 51
m2 103
b_low 0.919786096
b_up 1.456375839
a_low -196.0469799
a_up 50.21925134
Hello Jiri,
If you send me an Excel spreadsheet with your work, I will try to figure out what is going wrong.
Note that I have added a link on the webpage to the spreadsheet referenced on the webpage. This might help you find the problem yourself.
Charles
Hello, Charles. Meanwhile I have found the bug (I think): it is in the version of Excel. When I run the same data in Excel365, the results were correct (a=-33.6). And I confirmed my finding somewhere on internet discussion about range-arguments in Excel functions (that they are sometimes troublesome). What works in Excel 2019 is to calculate all the differences (y-b*x) separately in a column and then calculate median of the column…. Surprisingly, Gnumeric 1.12.9 calculates the “range median” also identically incorrect.
Hello Jiri,
Wow, that is strange. I wonder why the results in Excel 365 are correct, but not in Excel 2019. Do you have any idea whether Microsoft is planning to fix the underlying bug?
Thanks for sharing this.
Charles
I tried to recreate this using my own data, but had one of the cells in the array resolve to “”. This generated a #NAME error which propagated to the b-up, b-low, a-up, and a-low cells. If I changed the “” to a number, it fixed everything and returned the same numbers (to the decimals shown on the screen anyway) as your Excel add in. You used 1000 and -1000 elsewhere, what should I use to replace the “”?
Thank you for a great web site.
Hi Curt,
What question mark “”? are you referring to?
Charles
I assembled the array with each cell having the formula =IF($D5>E$4,IF($B5E$2,IF($B5+$C5E$2+E$3,($C5-E$3)/($B5-E$2),””), IF($C5>E$3,1000,IF($C5<E$3,-1000,””))),””) Whenever the cell resolved to ”” Excel generated the #NAME error. If I altered the formula so that ”” is replaced by any number such as 1000 or -1000, no error was produced and the various P-B results were produced.
Hi Curt,
This is quite strange. I wonder why you would get a #NAME error (instead of some other type of error).
If you email me your spreadsheet, I will try to figure out why you are getting this result.
Charles
What is the reason for shifting the median to the right by the number of slopes that are smaller than minus 1?
Sorry, but I don’t understand what you are referring to.
Charles
hi Charles.
Apologies for the poor quality of my question.
And thank you for having explained PB.
When using Passing Bablok, the slope is calculated for XY pairs (excluding pairs where xi = xj or yi = jj) and then ranked low to high. The number of slopes with values < -1 are counted ( = K) but discarded. The median of remaining slopes is shifted to the right by K places and this is the median used. Why is the median shifted by K?
Hello Stephen,
See https://arxiv.org/pdf/1905.07649#:~:text=The%20Passing%2DBablok%20estimate%20is,x%20and%20y%20are%20interchangeable.
“The Passing-Bablok estimate is also given by the median of all slopes, but shifted by an offset K to ensure that x and y are interchangeable.”
Charles