Theorem 1: The best fit line for the points (x1, y1), …, (xn, yn) is given by
Proof: Our objective is to minimize
For any given values of (x1, y1), … (xn, yn), this expression can be viewed as a function of b and c. Calling this function g(b, c), by calculus, the minimum value occurs when the partial derivatives are zero.
Transposing terms and simplifying,
Since = 0, from the second equation we have c = ȳ, and from the first equation we have
The result follows since
Alternative Proof: This proof doesn’t require any calculus. We first prove the theorem for the case where both x and y have mean 0 and standard deviation 1. Assume the best fit line is y = bx + a, and so
for all i. Our goal is to minimize the following quantity
Now minimizing z is equivalent to minimizing z/n, which is
since x̄ = ȳ = 0. Now since a2 is non-negative, the minimum value is achieved when a = 0. Since we are considering the case where x and y have a standard deviation of 1, , and so expanding the above expression further we get
Now suppose b = r – e, then the above expression becomes
Now since e2 is non-negative, the minimum value is achieved when e = 0. Thus b = r – e = r. This proves that the best fitting line has the form y = bx + a where b = r and a = 0, i.e. y = rx.
We now consider the general case where the x and y don’t necessarily have a mean of 0 and a standard deviation of 1, and set
x′ = (x – x̄)/sx and y′ = (y – ȳ)/sy
Now x′ and y′ do have a mean of 0 and a standard deviation of 1, and so the line that best fits the data is y′ = rx′, where r = the correlation coefficient between x′ and y′. Thus the best fit line has form
or equivalently
where b = rsy/sx. Now note that by Property B of Correlation, the correlation coefficient for x and y is the same as that for x′ and y′, namely r.
The result now follows by Property 1. If there is a better fit line for x and y, it would produce a better fit line for x′ and y′, which would be a contradiction.
References
Soch, J. (2021) Proof: Ordinary least squares for simple linear regression
https://statproofbook.github.io/P/slr-ols
https://statproofbook.github.io/P/slr-ols2

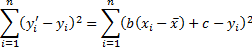
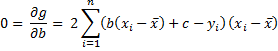
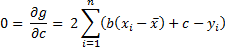
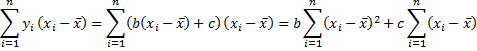
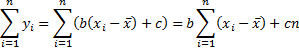
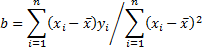
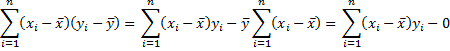
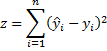
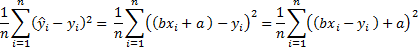
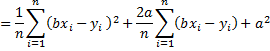
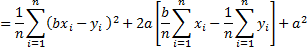
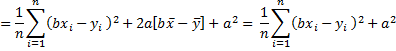
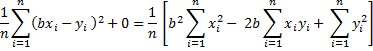
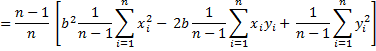
Thank you very much. This is not something that you can find in the usual textbooks.
why is sum(x-bar(x))= 0? please explain sir.
Hello Arshad,
First note that since xbar is a constant, sum(xbar) = n*xbar where n = size of data set. But xbar = sum(x_i)/n. so sum(xbar) = sum(x_i).
Now sum(x_i – xbar) = sum(x_i) – aum(xbar) = sum(x_i) – sum(x_i) = 0.
Charles
Hello Charlez! Thanks for such a good website,im happy that i’ve found it,its very helpfull!
I am doing researh “Does China consumption affect on world grain prices”
Time series from 1980-2017 year,using the eviews programm.My teacher said to use ADF Unit Root test,OLS test and Var regression.As i read in your article ADF unit root test needs to identify if the time series stationary or not,if its not stationary its mean that we reject the null hypotethis,am i right??? And still cant understand for what need to use Method of least Squares and Var?
Hello Alexandra,
If p-value < alpha (reject the null hypothesis) then the time series is stationary. See https://real-statistics.com/time-series-analysis/autoregressive-processes/augmented-dickey-fuller-test/
The Method of Least Squares is used in regression.
The website doesn’t support VAR regression yet.
Charles
Thank you Charles, I was looking everywhere for this Derivation!
Hi Charles,
Googling for a good answer on how to calculate the confidence limits of a linear regression I found your text. It is useful indeed.
Andreas