On this webpage, we show how to test whether the slopes for two independent populations are equal, i.e. we test the following null and alternative hypotheses:
H0: β1 = β2 i.e. β1 – β2 = 0
H1: β1 ≠ β2 i.e. β1 – β2 ≠ 0
The test statistic is
If the null hypothesis is true then
where
If the two error variances are equal, then as for the test for the differences in the means, we can pool the estimates of the error variances, weighing each by their degrees of freedom, and so
Now
Since we can replace the numerators of each by the pooled value 
Note that while the null hypothesis that β = 0 is equivalent to ρ = 0, the null hypothesis that β1 = β2 is not equivalent to ρ1 = ρ2.
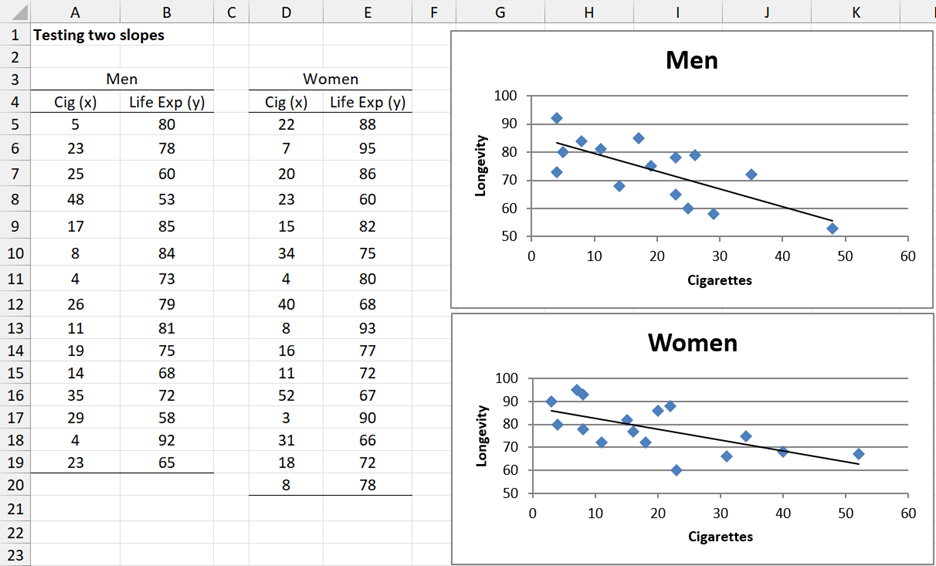
Example 1: We have two samples, each comparing life expectancy vs. smoking. The first sample is for males and the second for females. We want to determine whether there is any significant difference in the slopes for these two populations. We assume that the two samples have the values in Figure 1 (for men the data is the same as that in Example 1 of Regression Analysis):
Figure 1 – Data for Example 1
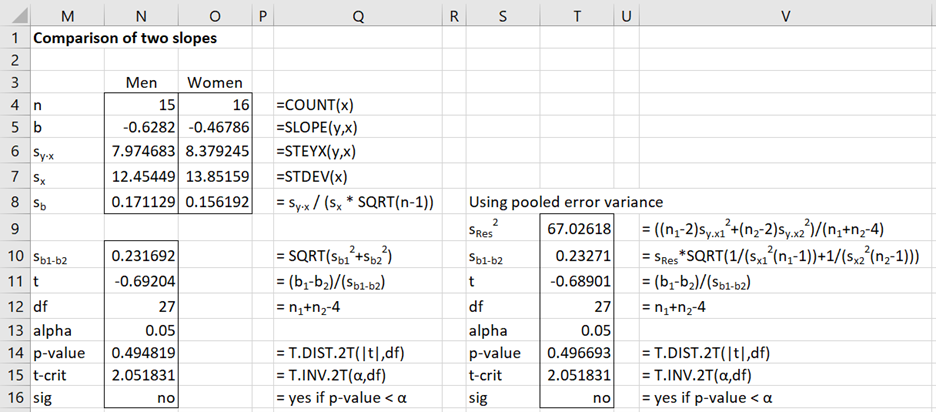
As can be seen from the scatter diagrams in Figure 1, it appears that the slope for women is less steep than for that for men. In fact, as can be seen from Figure 2, the slope of the regression line for men is -0.6282 and the slope for women is -0.4679, but is this difference significant?
As can be seen from the calculations in Figure 2, using both pooled and unpooled values for sRes, the null hypothesis, H0: the slopes are equal, cannot be rejected. And so we cannot conclude that there is any significant difference between the life expectancy of males and females for any incremental amount of smoking.
Figure 2 – t-test to compare slopes of regression lines
Real Statistics Function: The following array function is provided by the Real Statistics Resource Pack. Here Rx1, Ry1 are ranges containing the X and Y values for one sample and Rx2, Ry2 are the ranges containing the X and Y values for a second sample.
SlopesTest(Rx1, Ry1, Rx2, Ry2, b, lab): outputs the standard error of the difference in slopes sb1–b2, t, df and p-value for the test described above for comparing the slopes of the regression lines for the two samples.
If b = True (the default) then the pooled standard error sb1–b2 is used (as in cell T10 of Figure 2); otherwise the non-pooled standard error is used (as in cell N10 of Figure 2).
If lab = True then the output is a 4 × 2 range where the first column contains labels and the second column contains the values described above and if lab = False (the default) only the data is outputted (in the form of a 4 × 1 range).
The SlopesTest function only produces the correct results if there are no missing data elements in Rx1, Ry1, Rx2, Ry2.
Observation: For Example 1, the formula
=SlopesTest(A5:A19,B5:B19,D5:D20,E5:E20,FALSE,TRUE)
generates the output in range M30:N33 of Figure 3, while the formula
=SlopesTest(A5:A19,B5:B19,D5:D20,E5:E20)
generates the output in range O30:O33.
Figure 3 – Comparing slopes using SlopesTest function
Thank you for your work Charles. I have applied this data to the following values
X. Y 1 X Y2
1 38 1 5717089
2 1345 2 5540247
3 2428 3 5591382
4 2751 4 5381358
5 2510 5 5761455
The slopes for these two independent samples are very different, but the p-value I keep getting is 0.89, thought the slopes for both are drastically different, 635 and -7015 respectively. Any real statistics test you recommend to address this?
Th
Hello Blake,
This does seem surprising. I tried to repeat the analysis using the approach described at
https://real-statistics.com/multiple-regression/comparing-slopes-and-intercepts/
and unsurpringly I got the same result.
I am not sure why we get this non-intuitive result. Perhaps it is because the sample is so small.
Charles
Hello,
I installed the package successfully, but when I tried to compute the function =SlopesTest(A5:A19,B5:B19,D5:D20,E5:E20), it only gave me a single value as an output, not a whole output range, as depicted above in figure 3. Do you have an idea of what went wrong?
Best,
Jana
Hello Jana,
SlopesTest is what EXcel calls an array function. To get the full output you can-t simply press Enter. See the following webpage for how to use an array function:
https://real-statistics.com/array-formulas-functions/
Charles
I tried the command =SlopesTest(A5:A19,B5:B19,D5:D20,E5:E20) but the output is #NAME? . Where did it went wrong?
Hello Mark,
You need to install Real Statistics to use this formula. You can download the software from
https://real-statistics.com/free-download/real-statistics-resource-pack/
The software is free to use.
Charles
I had the same problem and my issue was security not trusting the add-in. I finally solved it by finding which folders were trusted in “Trusted Locations” and putting the add-in there. Then adding it from that location (which replaced the old location).
Charles, Thanks for showing us how to do this.
Randy
Hi Randy,
Glad to see that you were able to overcome this issue.
Charles
Hello, I would like to ask a question about the application.
I want to use this method to describe the difference between two calibration curves.
These two calibration curves use the same concentration and instrument, but use different substrates.
The results of my attempts so far show that none of the calibration lines are significantly different, even if the slopes differ by more than a factor of two. (N of calibration curve is 5)
Hello. Sorry, but I don’t know enough about this situation to address this issue.
Charles
Theoretically, what is the difference between this and F test, and how is this more advantageous ?
Albert,
Which F test are you referring to?
Charles
Hi Charles,
Thanks for all this great information. I just performed this test to determine the differences between slopes in two groups. Now I’m trying to figure out how best to report this in the methods. Is there a formula or a best practice on how to write this up in the results.
Thank you,
Manda
Manda,
I don’t know of a standard way to write up these results. I tend to copy the APA approach for the test that is most similar.
Charles
Hi, Charles.
I want to compare slopes between different levels of a 2 x 2 factorial design. One of the factor is Exersice (YES/NO) and the other factor is Diet (1/2).
For each combination of factor’s levels, I have measured Height (Y, dependent variable); X (age). I want to know if the slopes of the linear regression aplied to Y vs X, depend on the Exersice factor, or on the Diet factor, or may be on the interaction Exercise*Diet.
Is there a method for testing that?
Thank!
Leonardo
Leornardo,
If you can transform the problem about contingency tables into a regression issue, then you can use the approach decribed on this webpage.
Charles
Dear Charles,
I was wondering how you would describe this test in your methods. I can see that you are using two unequal samples, therefore, I was wondering whether you are using the Welch t-test?
Best,
Amanda
Amanda,
It doesn’t look like Welch’s t-test since the degrees of freedom are not changed.
Charles
Dear Charles,
I have a question that seems related to the test of the slopes of two independent populations.
I have two independent time-varying signals. Each of these signals has been measured multiple times. The time-varying signal is not linear with time, but slowly changing with time. I want to test the slopes of these two time-varying signals at different times. The hypothesis is the slope of one signal is always greater than the other.
My plan is to use something similar to your SlopeTest function, but limit the range to a certain time window, for example, 100 data points over time. Then apply SlopeTest at all different time positions to get test results over time.
I am wondering if this is logical? or are there any better way of doing this?
Many thanks,
The approach makes sense, but I don’t know whether this approach addresses the issue that you have.
Charles
Hi Charles,
Comparing slopes of two independent samples interests me very much, however, I need to compare slopes of three ind. samples as well. Can I add the 3rd sample group and its statistical parameters like below?
‘= (………..+(n3-2)sy.x32)/(…..+n3-(4+2))
‘= sRes*SQRT(1/(sx12(n1-1))+……+1/(sx32(n3-1)))
‘= (b1-b2-b3)/(sb1-b2-b3)
‘= n1+n2+n3-(4+2)
etc..
If is not as the way as I thought as above. Would you kindly provide how can we compare slopes of three ind. samples?
Thank you and appreciate very much!
Thuy
Hello Thuy,
I don’t know whether the approach that you are proposing works, but the following webpage provides an approach that will do the job:
https://stats.stackexchange.com/questions/232040/ways-of-comparing-linear-regression-interepts-and-slopes
I will add this explanation and an example to the Real Statistics website shortly.
Charles
Installed and trying to run SlopesTest. No missing data or anything, but the output is just the single term “std err”. How come I’m not seeing the rest of the output?
Randy,
SlopesTest is an array function and so you need to use it as described at
Array Formulas and Functions
Charles
Ah, never used CSE functions before. Just needed to press CSE at the end of the formula! Worked like a charm! Thanks,
rmc
Charles:
How would you go about comparing the intercepts for two independent samples?
Regards,
Bill
Bill,
See http://core.ecu.edu/psyc/wuenschk/docs30/CompareCorrCoeff.pdf
Charles
Thank you.
Hi Charles.
Thanks for the article. I’m completely green with statistics. Just trying to figure out a test that works for a school paper. I wonder if it makes sense to perform an ANOVA test on slopes to see if there is a difference in the mean of slopes between groups.
The use case is this. I’m trying to compare the slopes of time series of company share prices between groups. Each group has a different characteristic and about 5 companies in them. The statistic is meant to tell if the distinguishing charasteric influenced the steepness of the movement in shareprices between groups, by determining If there is a difference in the mean of the slopes.
I’m however worried if the slopes are directly comparable in such a manner. The size each company’s shares seems to influence how big the slope’s number is (A company with an average share price of 1000 CU gets of slope of about -200 while one with 10 CU get a slope of about -3). I was wondering if there was a way to treat the slopes to make them more comparable before running them through ANOVA or T-test. I had thought of expressing the slope as a percentage of the intercept. I wondered though if that made sense to an actual statistician.
Thanks again, Mr Charles.
Hello Benedict,
How many groups are you comparing? Are the 5 companies in each group selected at random?
Charles
Thanks for the reply, Mr Charles. Yes, there are about 4 in each group. Not really random as it is the population of listed UK banks. They have been distinguished into groups by a qualitatively derived score.
I have my doubts about using ANOVA in this case.
Charles
Is there a test you could recommend?
Dear Charles,
Thank you very much for your stat pack.
I am running this slope test but does not work for me. I installed satisfactory the pack and can open it on the add-on. Then, I clicked on regression tab but I do not see the slope test. Finally, I used =SlopesTest(A5:A19,B5:B19,D5:D20,E5:E20) as example in my data set changing data ranges accordingly. Is there any other way to perform this test using the pack?
Best regards,
Ramiro
Ramiro,
Currently, you can only perform this test using the SlopesTest function.
Charles
Hi, Mr.Charles,
I cannot understand about the degree of freedom.
Why are you using -4??
In this case, I think Men=15-1, Women=16-1, so, “df”is n1-1+n2-1 (= n1+n2-2)?
This just how the mathematics turns out. The intuitive answer is that there are 4 variables: men and women for sample 1 and men and women for sample 2.
Charles
Hello. I am looking to use a test like this to assess the probability of similarity between two groups of bivatiate data. I tried this slope test in Excel and got it to work. If I am reporting the results, how should I refer to the test? I think I can figure out how to report the results, but I’m not sure what type of test I should say that I used. Also, are there any additional tests that might be more appropriate? I am comparing the density and porosity of stone to assess the probability that the relationship of density to porosity is the same between two groups. Thanks!
Hi Mike,
I got this test from Howell’s textbook (see Bibliography). No fancy name is given. I would call it
Testing the difference between the slopes from two independent samples.
I don’t know of other tests that do this.
Charles
Good day, I want to compare stadisticaly diferent calibration curves in order to evaluate the standard stability in diferent day. How can I do this?
Hello Paola,
I need to additional context in order to answer your question. What sort of calibration curves are you referring to and what do you mean by standard stability?
Charles
How do I access this test within the Resources Toolpack?- Thanks for all your help
Hello Curran,
You download it from Real Statistics Resource Pack and then install the software as described on that webpage.
You can then access the data analysis tools by pressing the key sequence Ctrl-m.
Charles
Good evening Charles:
I’m having the same issue as Curran.
I’ve installed the software as described, it appears in the Excel add-ins and the box is checked. I cannot find it in any of the Excel ribbon tabs, and Ctrl-m just generates a chime sound.
Any help will be appreciated.
Regards,
Bill
Hi Bill,
What do you see when you enter the formula =VER() in any cell on an Excel spreadsheet?
Charles
What is the name of this test?
I dont know the name of this test. You probably can call it the Slope Test for Two Independent Samples.
Charles
Thank you for this helpful page. Why have you used the same number of degrees of freedom for the unpooled and pooled methods? Shouldn’t the degrees of freedom for the unpooled case be different?
Hello Dave,
You may be correct, but why should the degrees of freedom be different? Do you have a reference for this?
Charles
Good morning Charles,
Thanks for your examples. When running the slopes test, I’m getting a significant difference between the groups’ respective slopes. However, when running the groups’ probability and z-scores using an on-line calculator, I’m getting a significant difference. Should this be happening or is this something that tends to occur? Thanks in advance.
Richard.
Hi Richard,
If you email me an Excel file with your data and calculations, I will try to figure out what is happening.
Charles
Using unpooled values our hypothesis would be
H0 : β1 − β2 = 0
and alternative is
Ha : β1 − β2 > 0
When you receive “sig = no” in figure 2, where you calculate the conlusion of the t.test for unpooled values, do you mean that slope 1 is not sig. bigger than slope 2 ?
Manuela,
The alternative hypothesis is Ha : β1 − β2 not equal to 0. If sig = no, then you can conclude that there is no evidence that slope 1 is significantly different from slope 2.
Charles
Hi Charles,
Thanks for this great pack!
I have the most current version of realstats loaded but somehow the slopestest function isn’t returning what’s referenced in Figure 3. I am just getting “st dev” or a single number e.g. 0.00298. Am I just missing something?
Charlie,
This function is an array function and so you can’t simply press the Enter key. It is easy to get the value, but the procedure is a bit different. See the following webpage:
Array Function
Charles
A child with no gifted and talented students in his or her school, would be predicted to have a reading test score of what?
0
.049
50.7
58.6
Dexter,
I don’t see how I could answer this question.
Charles